Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Analizy opisowe » Statystyka opisowa » Miary położenia
Pasek boczny
statpqpl:aopisowapl:statopispl:miarpl
Miary położenia
Miary tendencji centralnej
Miary tendencji centralnej są to tzw. miary przeciętne charakteryzujące średni lub typowy poziom wartości cechy.
Średnia arytmetyczna (ang. arithmetic mean) wyraża się wzorem:
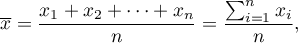
gdzie  to kolejne wartości zmiennej a
to kolejne wartości zmiennej a  - liczność próby.
- liczność próby.
Średnia arytmetyczna jest stosowana dla skali interwałowej. Dla próby przyjmuje się ją oznaczać przez 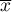 a dla populacji przez
a dla populacji przez 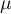 .
.
Średnia przycięta (Trimmed mean)- wyznaczana jest jako średnia arytmetyczna obliczona po usunięciu z próbki zadanego procentu najmniejszych i największych pomiarów np. gdy obcinamy 5% pomiarów, to oznacza, że obcinamy 2.5% największych i 2.5% najmniejszych wartości. Przy czym, gdy uzyskana na podstawie przeliczań liczba pomiarów przeznaczonych do usunięcia nie będzie liczbą całkowitą, wówczas jest ona zaokrąglana w dół do najbliższej całkowitej.
Średnia Winsora (Winsor mean) - wyznaczana jest jako średnia arytmetyczna obliczona po zastąpieniu odpowiedniego odsetka skrajnych pomiarów wartością najmniejszą i największą jaka pozostała zmniejszonym zbiorze wartości. Jeśli zdecydujemy się na obliczanie średniej Winsora przycinając np. 5% pomiarów, to wówczas te odrzucone 5% zostanie zastąpione wartością najmniejszą i największą wyznaczoną z pozostałych 95% pomiarów. Podobnie jak dla średniej przycinanej, gdy na podstawie przeliczenia procentu wartości przeznaczonych do zamiany na liczbę pomiarów przeznaczonych do zamiany nie uzyskamy liczby całkowitej, wówczas zaokrąglamy w dół do najbliższej całkowitej.
Średnia geometryczna (ang. geometric mean) wyraża się wzorem:
![LaTeX \begin{displaymath}
\overline{x}_G=\sqrt[n]{x_1x_2...x_n}=\sqrt[n]{\prod_{i=1}^n x_i}.
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img011017a5d163d0e6305611f865ade072.png) Średnia ta jest stosowana dla skali interwałowej, gdy zmienna ma rozkład logarytmiczno-normalny (logarytm zmiennej ma rozkład normalny).
Średnia ta jest stosowana dla skali interwałowej, gdy zmienna ma rozkład logarytmiczno-normalny (logarytm zmiennej ma rozkład normalny).
Średnia harmoniczna (ang. harmonic mean) wyraża się wzorem:
 Średnia ta jest stosowana dla skali interwałowej.
Średnia ta jest stosowana dla skali interwałowej.
W uporządkowanym zbiorze danych mediana jest wartością dzielącą ten zbiór na dwie równe części. Połowa wszystkich obserwacji znajduje się poniżej, a połowa powyżej mediany.
![LaTeX \begin{pspicture}(0,0)(10,10.6)
\pscoil[coilaspect=0, coilarm=.1cm, linewidth=0.5pt, coilwidth=.5cm, coilheight=1]{-}(0,4)
\rput(0,4.2){min}
\rput(0,-.2){max}
\psline(-0.35,2)(.35,2)
\rput(1.2,2){mediana}
\rput(-0.6,2.8){50$\%$}
\rput(-0.6,1.2){50$\%$}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img826223981ace04d4f37d432b7063428a.png)
Mediana może być stosowana w skali interwałowej oraz porządkowej.
Moda  jest to wartość, która występuje najczęściej wśród uzyskanych pomiarów. Moda może być stosowana w każdej skali pomiarowej.
jest to wartość, która występuje najczęściej wśród uzyskanych pomiarów. Moda może być stosowana w każdej skali pomiarowej.
2022/01/23 17:58
· admin
Inne miary położenia
kwartyle (ang. quartiles), decyle (ang. deciles), centyle (ang. centiles)
![LaTeX \begin{pspicture}(0,-.2)(4,4.4)
\pscoil[coilaspect=0, coilarm=.1cm, linewidth=0.5pt, coilwidth=.5cm, coilheight=1]{-}(0,4)
\rput(0,4.2){max}
\rput(0,-.2){min}
\psline(-0.35,3)(.35,3)
\psline(-0.35,2)(.35,2)
\psline(-0.35,1)(.35,1)
\rput(2.9,3){$C_{75}$ = kwartyl górny = $Q_3$}
\rput(2.4,2){$C_{50}$ = mediana = $Q_2$}
\rput(2.9,1){$C_{25}$ = kwartyl dolny = $Q_1$}
\rput(1,3.5){25$\%$}
\rput(1,2.5){25$\%$}
\rput(1,1.5){25$\%$}
\rput(1,.5){25$\%$}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img95cc67a481e2d6314660a8aa6c567235.png)
Kwartyle (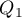 ,
, 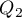 ,
, 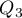 ) dzielą uporządkowany szereg na 4 równe części, decyle (
) dzielą uporządkowany szereg na 4 równe części, decyle (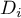 ,
, 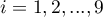 ) na 10 równych części a centyle (percentyle:
) na 10 równych części a centyle (percentyle: 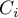 ,
, 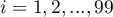 ) na 100 równych części. Drugi kwartyl, piąty decyl i pięćdziesiąty centyl są równe medianie. Miary te mogą być stosowane w skali interwałowej oraz porządkowej.
) na 100 równych części. Drugi kwartyl, piąty decyl i pięćdziesiąty centyl są równe medianie. Miary te mogą być stosowane w skali interwałowej oraz porządkowej.
2022/01/23 17:59
· admin
statpqpl/aopisowapl/statopispl/miarpl.txt · ostatnio zmienione: 2022/01/23 18:08 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

