Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:statpqpl:wielowympl:przygpl:kodpl
Variables coding
When preparing data for a multidimensional analysis there is the problem of appropriate coding of nominal and ordinal variables. That is an important element of preparing data for analysis as it is a key factor in the interpretation of the coefficients of a model. The nominal or ordinal variables divide the analyzed objects into two or more categories. The dichotomous variables (in two categories, 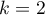 ) must only be appropriately coded, whereas the variables with many categories (
) must only be appropriately coded, whereas the variables with many categories (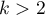 ) ought to be divided into dummy variables with two categories and coded.
) ought to be divided into dummy variables with two categories and coded.
- [
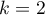 ] If a variable is dichotomous, it is the decision of the researcher how the data representing the variable will be entered, so any numerical codes can be entered, e.g. 0 and 1. In the program one can change one's coding into
] If a variable is dichotomous, it is the decision of the researcher how the data representing the variable will be entered, so any numerical codes can be entered, e.g. 0 and 1. In the program one can change one's coding into effect codingby selecting that option in the window of the selected multidimensional analysis. Such coding causes a replacement of the smaller value with value -1 and of the greater value with value 1. - [
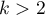 ] If a variable has many categories then in the window of the selected multidimensional analysis we select the button
] If a variable has many categories then in the window of the selected multidimensional analysis we select the button Dummy variablesand set the reference/base category for those variables which we want to break into dummy variables. The variables will be dummy coded unless theeffect codingoption will be selected in the window of the analysis – in such a case, they will be coded as -1, 0, and 1.
Dummy coding is employed in order to answer, with the use of multidimensional models, the question: How do the ( ) results in any analyzed category differ from the results of the reference category. The coding consists in ascribing value 0 or 1 to each category of the given variable. The category coded as 0 is, then, the reference category.
) results in any analyzed category differ from the results of the reference category. The coding consists in ascribing value 0 or 1 to each category of the given variable. The category coded as 0 is, then, the reference category.
- [
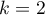 ] If the coded variable is dichotomous, then by placing it in a regression model we will obtain the coefficient calculated for it, (
] If the coded variable is dichotomous, then by placing it in a regression model we will obtain the coefficient calculated for it, (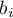 ). The coefficient is the reference of the value of the dependent variable
). The coefficient is the reference of the value of the dependent variable  for category 1 to the reference category (corrected with the remaining variables in the model).
for category 1 to the reference category (corrected with the remaining variables in the model). - [
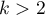 ] If the analyzed variable has more than two categories, then
] If the analyzed variable has more than two categories, then  categories are represented by
categories are represented by 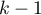 dummy variables with dummy coding. When creating variables with dummy coding one selects a category for which no dummy category is created. That category is treated as a reference category (as the value of each variable coded in the dummy coding is equal to 0.
dummy variables with dummy coding. When creating variables with dummy coding one selects a category for which no dummy category is created. That category is treated as a reference category (as the value of each variable coded in the dummy coding is equal to 0.
When the 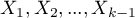 variables obtained in that way, with dummy coding, are placed in a regression model, then their
variables obtained in that way, with dummy coding, are placed in a regression model, then their  coefficients will be calculated.
coefficients will be calculated.
- [
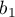 ] is the reference of the
] is the reference of the  results (for codes 1 in
results (for codes 1 in 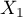 ) to the reference category (corrected with the remaining variables in the model);
) to the reference category (corrected with the remaining variables in the model); - [
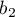 ] is the reference of the
] is the reference of the  results (for codes 1 in
results (for codes 1 in 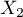 ) to the reference category (corrected with the remaining variables in the model);
) to the reference category (corrected with the remaining variables in the model); - […]
- [
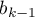 ] is the reference of the
] is the reference of the  results (for codes 1 in
results (for codes 1 in 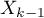 ) to the reference category (corrected with the remaining variables in the model);
) to the reference category (corrected with the remaining variables in the model);
Example
We code, in accordance with dummy coding, the sex variable with two categories (the male sex will be selected as the reference category), and the education variable with 4 categories (elementary education will be selected as the reference category).
![LaTeX \mbox{\begin{tabular}{|c|c|}
\hline
&\textcolor[rgb]{0.5,0,0.5}{\textbf{Coded}}\\
\textbf{Sex}&\textcolor[rgb]{0.5,0,0.5}{\textbf{sex}}\\\hline
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}0\\
...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img64f9c549e24e01a1c45aee7f0c4dbb3e.png)
![LaTeX \mbox{\begin{tabular}{|c|ccc|}
\hline
& \multicolumn{3}{c|}{\textbf{Coded education}}\\
\textbf{Education}&\textcolor[rgb]{0,0,1}{\textbf{vocational}}&\textcolor[rgb]{1,0,0}{\textbf{secondary}}&\textcolor[rgb]{0,0.58,0}{\textbf{tertiary}}\\\hline
\cellcolor[rgb]{0.88,0.88,0.88}elementary&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}elementary&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\cellcolor[rgb]{0.88,0.88,0.88}elementary&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0&\cellcolor[rgb]{0.88,0.88,0.88}0\\
\textcolor[rgb]{0,0,1}{vocational}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{0,0,1}{vocational}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{0,0,1}{vocational}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{0,0,1}{vocational}&\textcolor[rgb]{0,0,1}{1}&0&0\\
\textcolor[rgb]{1,0,0}{secondary}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{1,0,0}{secondary}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{1,0,0}{secondary}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{1,0,0}{secondary}&0&\textcolor[rgb]{1,0,0}{1}&0\\
\textcolor[rgb]{0,0.58,0}{tertiary}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
\textcolor[rgb]{0,0.58,0}{tertiary}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
\textcolor[rgb]{0,0.58,0}{tertiary}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\\
\textcolor[rgb]{0,0.58,0}{tertiary}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
\textcolor[rgb]{0,0.58,0}{tertiary}&0&0&\textcolor[rgb]{0,0.58,0}{1}\\
...&...&...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/imgbfcf0cf803285f0ed297510006e88698.png)
Building on the basis of dummy variables, in a multiple regression model, we might want to check what impact the variables have on a dependent variable, e.g.  = the amount of earnings (in thousands of PLN). As a result of such an analysis we will obtain sample coefficients for each dummy variable:
= the amount of earnings (in thousands of PLN). As a result of such an analysis we will obtain sample coefficients for each dummy variable:
- for sex the statistically significant coefficient 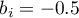 , which means that average women's wages are a half of a thousand PLN lower than men's wages, assuming that all other variables in the model remain unchanged;
, which means that average women's wages are a half of a thousand PLN lower than men's wages, assuming that all other variables in the model remain unchanged;
- for vocational education the statistically significant coefficient 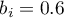 , which means that the average wages of people with elementary education are 0.6 of a thousand PLN higher than those of people with elementary education, assuming that all other variables in the model remain unchanged;
, which means that the average wages of people with elementary education are 0.6 of a thousand PLN higher than those of people with elementary education, assuming that all other variables in the model remain unchanged;
- for secondary education the statistically significant coefficient 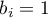 , which means that the average wages of people with secondary education are a thousand PLN higher than those of people with elementary education, assuming that all other variables in the model remain unchanged;
, which means that the average wages of people with secondary education are a thousand PLN higher than those of people with elementary education, assuming that all other variables in the model remain unchanged;
- for tertiary-level education the statistically significant coefficient 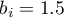 , which means that the average wages of people with tertiary-level education are 1.5 PLN higher than those of people with elementary education, assuming that all other variables in the model remain unchanged;
, which means that the average wages of people with tertiary-level education are 1.5 PLN higher than those of people with elementary education, assuming that all other variables in the model remain unchanged;
Effect coding is used to answer, with the use of multidimensional models, the question: How do ( ) results in each analyzed category differ from the results of the (unweighted) mean obtained from the sample. The coding consists in ascribing value -1 or 1 to each category of the given variable. The category coded as -1 is then the base category
) results in each analyzed category differ from the results of the (unweighted) mean obtained from the sample. The coding consists in ascribing value -1 or 1 to each category of the given variable. The category coded as -1 is then the base category
- [
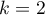 ] If the coded variable is dichotomous, then by placing it in a regression model we will obtain the coefficient calculated for it, (
] If the coded variable is dichotomous, then by placing it in a regression model we will obtain the coefficient calculated for it, (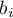 ). The coefficient is the reference of
). The coefficient is the reference of  for category 1 to the unweighted general mean (corrected with the remaining variables in the model).
for category 1 to the unweighted general mean (corrected with the remaining variables in the model). - If the analyzed variable has more than two categories, then
 categories are represented by
categories are represented by 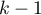 dummy variables with effect coding. When creating variables with effect coding a category is selected for which no separate variable is made. The category is treated in the models as a base category (as in each variable made by effect coding it has values -1).
dummy variables with effect coding. When creating variables with effect coding a category is selected for which no separate variable is made. The category is treated in the models as a base category (as in each variable made by effect coding it has values -1).
When the 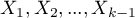 variables obtained in that way, with effect coding, are placed in a regression model, then their
variables obtained in that way, with effect coding, are placed in a regression model, then their  coefficients will be calculated.
coefficients will be calculated.
- [
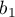 ] is the reference of the
] is the reference of the  results (for codes 1 in
results (for codes 1 in 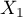 ) to the unweighted general mean (corrected by the remaining variables in the model);
) to the unweighted general mean (corrected by the remaining variables in the model); - [
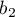 ] is the reference of the
] is the reference of the  results (for codes 1 in
results (for codes 1 in 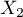 ) to the unweighted general mean (corrected by the remaining variables in the model);
) to the unweighted general mean (corrected by the remaining variables in the model); - […]
- [
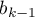 ] is the reference of the
] is the reference of the  results (for codes 1 in
results (for codes 1 in 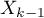 ) to the unweighted general mean (corrected by the remaining variables in the model);
) to the unweighted general mean (corrected by the remaining variables in the model);
Example
With the use of effect coding we will code the sex variable with two categories (the male category will be the base category) and a variable informing about the region of residence in the analyzed country. 5 regions were selected: northern, southern, eastern, western, and central. The central region will be the base one.
![LaTeX \mbox{\begin{tabular}{|c|c|}
\hline
&\textcolor[rgb]{0.5,0,0.5}{\textbf{Coded}}\\
\textbf{Sex}&\textcolor[rgb]{0.5,0,0.5}{\textbf{sex}}\\\hline
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
f&\textcolor[rgb]{0.5,0,0.5}{1}\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}m&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img1352d8cc71ff450a436fe12d8d8f68a9.png)
![LaTeX \mbox{\begin{tabular}{|c|cccc|}
\hline
\textbf{Regions}& \multicolumn{4}{c|}{\textbf{Coded regions}}\\
\textbf{of residence}&\textcolor[rgb]{0,0,1}{\textbf{western}}&\textcolor[rgb]{1,0,0}{\textbf{eastern}}&\textcolor[rgb]{0,0.58,0}{\textbf{northern}}&\textcolor[rgb]{0.55,0,0}{\textbf{southern}}\\\hline
\cellcolor[rgb]{0.88,0.88,0.88}central&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}central&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\cellcolor[rgb]{0.88,0.88,0.88}central&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1&\cellcolor[rgb]{0.88,0.88,0.88}-1\\
\textcolor[rgb]{0,0,1}{western}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{0,0,1}{western}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{0,0,1}{western}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{0,0,1}{western}&\textcolor[rgb]{0,0,1}{1}&0&0&0\\
\textcolor[rgb]{1,0,0}{eastern}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{1,0,0}{eastern}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{1,0,0}{eastern}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{1,0,0}{eastern}&0&\textcolor[rgb]{1,0,0}{1}&0&0\\
\textcolor[rgb]{0,0.58,0}{northern}&0&0&\textcolor[rgb]{0,0.58,0}{1}&0\\
\textcolor[rgb]{0,0.58,0}{northern}&0&0&\textcolor[rgb]{0,0.58,0}{1}&0\\
\textcolor[rgb]{0.55,0,0}{southern}&0&0&0&\textcolor[rgb]{0.55,0,0}{1}\\
\textcolor[rgb]{0.55,0,0}{southern}&0&0&0&\textcolor[rgb]{0.55,0,0}{1}\\
\textcolor[rgb]{0.55,0,0}{southern}&0&0&0&\textcolor[rgb]{0.55,0,0}{1}\\
...&...&...&...&...\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img280b4cd6d13af15399acda93337d241b.png)
Building on the basis of dummy variables, in a multiple regression model, we might want to check what impact the variables have on a dependent variable, e.g.  = the amount of earnings (expressed in thousands of PLN). As a result of such an analysis we will obtain sample coefficients for each dummy variable:
= the amount of earnings (expressed in thousands of PLN). As a result of such an analysis we will obtain sample coefficients for each dummy variable:
- for sex the statistically significant coefficient 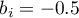 , which means that the average women's wages are a half of a thousand PLN lower than the average wages in the country, assuming that the other variables in the model remain unchanged;
, which means that the average women's wages are a half of a thousand PLN lower than the average wages in the country, assuming that the other variables in the model remain unchanged;
- for the western region the statistically significant coefficient 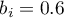 , which means that the average wages of people living in the western region of the country are 0.6 thousand PLN higher than the average wages in the country, assuming that the other variables in the model remain unchanged;
, which means that the average wages of people living in the western region of the country are 0.6 thousand PLN higher than the average wages in the country, assuming that the other variables in the model remain unchanged;
- for the eastern region the statistically significant coefficient  , which means that the average wages of people living in the eastern region of the country are a thousand PLN lower than the average wages in the country, assuming that the other variables in the model remain unchanged;
, which means that the average wages of people living in the eastern region of the country are a thousand PLN lower than the average wages in the country, assuming that the other variables in the model remain unchanged;
- for the northern region the statistically significant coefficient 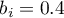 , which means that the average wages of people living in the western region of the country are 0.4 thousand PLN higher than the average wages in the country, assuming that the other variables in the model remain unchanged;
, which means that the average wages of people living in the western region of the country are 0.4 thousand PLN higher than the average wages in the country, assuming that the other variables in the model remain unchanged;
- for the southern region the statistically significant coefficient 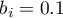 , which means that the average wages of people living in the southern region of the country do not differ in a statistically significant manner from the average wages in the country, assuming that the other variables in the model remain unchanged;
, which means that the average wages of people living in the southern region of the country do not differ in a statistically significant manner from the average wages in the country, assuming that the other variables in the model remain unchanged;
en/statpqpl/wielowympl/przygpl/kodpl.txt · ostatnio zmienione: 2022/02/26 15:36 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

