Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:statpqpl:redpl:pcapl:grafpl
Graphical interpretation
A lot of information carried by the coefficients returned in the tables can be presented on one chart. The ability to read charts allows a quick interpretation of many aspects of the conducted analysis. The charts gather in one place the information concerning the mutual relationships among the components, the original variables, and the cases. They give a general picture of the principal components analysis which makes them a very good summary of it.
Factor loadings graph
The graph shows vectors connected with the beginning of the coordinate system, which represent original variables. The vectors are placed on a plane defined by the two selected principal components.
{3}
\psline{->}(0,0)(2.5,1)
\rput(2.5,0.8){A}
\psline{->}(0,0)(2.7,1.3)
\rput(2.4,1.43){B}
\psline{->}(0,0)(1,1)
\rput(0.7,1){C}
\psline{->}(0,0)(-1.5,0.3)
\rput(-1.4,0.5){D}
\psline{->}(0,0)(-2,-2)
\rput(-2,-1.7){E}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imga791b18820caf03e86415963084a97c1.png)
- The coordinates of the terminal points of the vector are the corresponding factor loadings of the variables.
- Vector length represents the information content of an original variable carried by the principal components which define the coordinate system. The longer the vector the greater the contribution of the original variable to the components. In the case of an analysis based on a correlation matrix the loadings are correlations between original variables and principal components. In such a case points fall into the unit circle. It happens because the correlation coefficient cannot exceed one. As a result, the closer a given original variable lies to the rim of the circle the better the representation of such a variable by the presented principal components.
- The sign of the coordinates of the terminal point of the vector i.e. the sign of the loading factor, points to the positive or negative correlation of an original variable and the principal components forming the coordination system. If we consider both axes (2 components) together then original variables can fall into one of four categories, depending on the combination of signs (
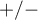 ) and their loading factors.
) and their loading factors. - The angle between vectors indicates the correlation of original values:
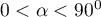 – the smaller the angle between the vectors representing original variables, the stronger the positive correlation among these variables.
– the smaller the angle between the vectors representing original variables, the stronger the positive correlation among these variables.
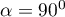 – the vectors are perpendicular, which means that the original variables are not correlated.
– the vectors are perpendicular, which means that the original variables are not correlated.
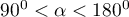 – the greater the angle between the vectors representing the original variables, the stronger the negative correlation among these variables.
– the greater the angle between the vectors representing the original variables, the stronger the negative correlation among these variables.
Biplot
The graph presents 2 series of data placed in a coordinate system defined by 2 principal components. The first series on the graph are data from the first graph (i.e. the vectors of original variables) and the second series are points presenting particular cases.

\psdot[dotsize=3pt](0.8,0)
\psdot[dotsize=3pt](1.1,0.2)
\psdot[dotsize=3pt](2,-1.6)
\psdot[dotsize=3pt](1.3,0)
\psdot[dotsize=3pt](-1.6,1.9)
\psdot[dotsize=3pt](-1.2,-1)
\psdot[dotsize=3pt](1.3,0.5)
\psdot[dotsize=3pt](1,0.6)
\psdot[dotsize=3pt](0.2,-1.6)
\psdot[dotsize=3pt](-0.6,0.2)
\psdot[dotsize=3pt](-0.8,-1)
\psdot[dotsize=3pt](1.9,0.7)
\psdot[dotsize=3pt](1.8,-1.2)
\psdot[dotsize=3pt](-1.8,-1)
\psdot[dotsize=3pt](1.4,0.8)
\psdot[dotsize=3pt](-0.6,-1.8)
\psdot[dotsize=3pt](1.1,0.3)
\psdot[dotsize=3pt](0.1,-1)
\psdot[dotsize=3pt](-1.7,-1)
\psdot[dotsize=3pt](1,-0.2)
\psdot[dotsize=3pt](-0.4,-1.3)
\psdot[dotsize=3pt](-1.1,-0.2)
\psdot[dotsize=3pt](-0.1,-0.3)
\psdot[dotsize=3pt](0.9,-0.9)
\psdot[dotsize=3pt](-0.1,0.5)
\psdot[dotsize=3pt](2,1.9)
\psdot[dotsize=3pt](-1.5,-1)
\psdot[dotsize=3pt](-1.5,1.1)
\psdot[dotsize=3pt](0.6,-0.6)
\psline{->}(0,0)(2.5,1)
\rput(2.5,0.8){A}
\psline{->}(0,0)(2.7,1.3)
\rput(2.4,1.43){B}
\psline{->}(0,0)(1,1)
\rput(0.7,1){C}
\psline{->}(0,0)(-1.5,0.3)
\rput(-1.4,0.5){D}
\psline{->}(0,0)(-2,-2)
\rput(-2,-1.7){E}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img2b39b527c98bf4a4b17471e1b7b9c745.png)
- Point coordinates should be interpreted as standardized values, i.e. positive coordinates pointing to a value higher than the mean value of the principal component, negative ones to a lower value, and the higher the absolute value the further the points are from the mean. If there are untypical observations on the graph, i.e. outliers, they can disturb the analysis and should be removed, and the analysis should be made again.
- The distances between the points show the similarity of cases: the closer (in the meaning of Euclidean distance) they are to one another, the more similar information is carried by the compared cases.
- Orthographic projection of points on vectors are interpreted in the same manner as point coordinates, i.e. projections onto axes, but the interpretation concerns original variables and not principal components. The values placed at the end of a vector are greater than the mean value of the original variable, and the values placed on the extension of the vector but in the opposite direction are values smaller than the mean.
EXAMPLE cont. (iris.pqs file)
en/statpqpl/redpl/pcapl/grafpl.txt · ostatnio zmienione: 2022/02/16 09:21 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

