Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:statpqpl:porown3grpl:parpl:levenepl
The Brown-Forsythe test and the Levene test
Both tests: the Levene test (Levene, 1960 1)) and the Brown-Forsythe test (Brown and Forsythe, 1974 2)) are used to verify the hypothesis determining the equality of variance of an analysed variable in several (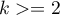 ) populations.
) populations.
Basic assumptions:
- measurement on an interval scale,
- normality of distribution of an analysed feature in each population,
Hypotheses:
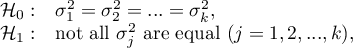
where:
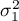 ,
,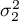 ,…,
,…,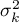
 variances of an analysed variable of each population.
variances of an analysed variable of each population.
The analysis is based on calculating the absolute deviation of measurement results from the mean (in the Levene test) or from the median (in the Brown-Forsythe test), in each of the analysed groups. This absolute deviation is the set of data which are under the same procedure performed to the analysis of variance for independent groups. Hence, the test statistic is defined by:
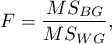
The test statistic has the F Snedecor distribution with 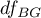 and
and 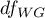 degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Note
The Brown-Forsythe test is less sensitive than the Levene test, in terms of an unfulfilled assumption relating to distribution normality.
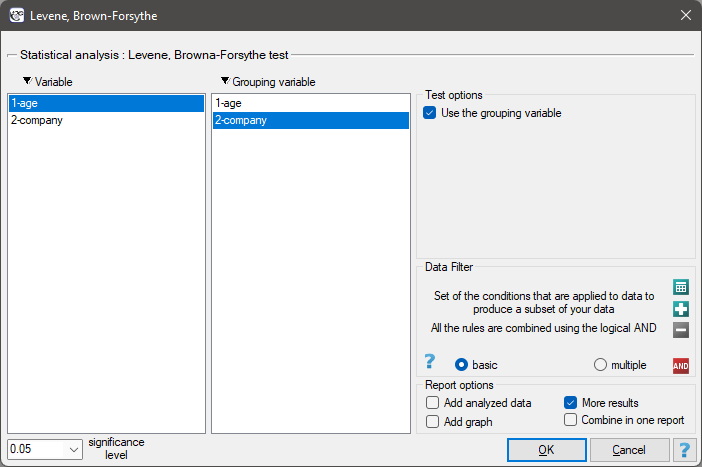
The settings window with the Levene, Brown-Forsythe tests' can be opened in Statistics menu→Parametric tests→Levene, Brown-Forsythe.
1)
Levene H. (1960), Robust tests for the equality of variance. In I. Olkin (Ed.) Contributions to probability and statistics (278-292). Palo Alto, CA: Stanford University Press
2)
Brown M.B., Forsythe A. B. (1974a), Robust tests for equality of variances. Journal of the American Statistical Association, 69,364-367
en/statpqpl/porown3grpl/parpl/levenepl.txt · ostatnio zmienione: 2022/02/13 11:27 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

