PQStat - Baza Wiedzy

The Chi-square test corrections for small tables

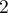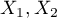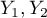These tests are based on data collected in the form of a contingency table of 2 features ( $X$ , $Y$ ), each of which has possible $2$ categories $X_1, X_2$ and $Y_1, Y_2$ (look at the table(\ref{tab_kontyngencji_obser})).

The Chi-square test with the Yate's correction for continuity

The $\chi^2$ test with the Yate's correction (Frank Yates (1934)¹⁾) is a more conservative test than the Chi-square test (it rejects a null hypothesis more rarely than the $\chi^2$ test). The correction for continuity guarantees the possibility of taking in all the values of real numbers by a test statistic, according to the $\chi^2$ distribution assumption.

The test statistic is defined by:

$\begin{displaymath} \chi^2=\sum_{i=1}^2\sum_{j=1}^2\frac{(|O_{ij}-E_{ij}|-0.5)^2}{E_{ij}}. \end{displaymath}$

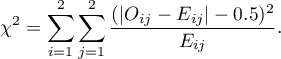
The Fisher test for (2×2) tables

The Fisher test for 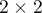$2\times 2$ tables is also called the Fisher exact test (R. A. Fisher (1934)²⁾, (1935)³⁾). This test enables you to calculate the exact probability of the occurrence of the particular number distribution in a table (knowing $n$ and defined marginal sums.

$\begin{displaymath} P=\frac{{O_{11}+O_{21} \choose O_{11}}{O_{12}+O_{22} \choose O_{12}}}{{O_{11}+O_{12}+O_{21}+O_{22} \choose O_{11}+O_{12}}}. \end{displaymath}$

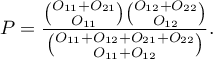
If you know each marginal sum, you can calculate the 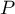$P$ probability for various configurations of observed frequencies. The exact $p$ significance level is the sum of probabilities which are less or equal to the analysed probability.

The mid-p test

The mid-p is the Fisher exact test correction. This modified p-value is recommended by many statisticians (Lancaster 1961⁴⁾, Anscombe 1981⁵⁾, Pratt and Gibbons 1981⁶⁾, Plackett 1984⁷⁾, Miettinen 1985⁸⁾ and Barnard 1989⁹⁾, Rothman 2008¹⁰⁾) as a method used in decreasing the Fisher exact test conservatism. As a result, using the mid-p the null hypothesis is rejected much more qucikly than by using the Fisher exact test. For large samples a p-value is calculated by using the $\chi^2$ test with the Yate's correction and the Fisher test gives quite similar results. But a p-value of the $\chi^2$ test without any correction corresponds with the mid-p.

The p-value of the mid-p is calculated by the transformation of the probability value for the Fisher exact test. The one-sided p-value is calculated by using the following formula:

$\begin{displaymath} p_{I(mid-p)}=p_{I(Fisher)}-0.5\cdot P_{punktu(tabeli\quad zadanej)}, \end{displaymath}$

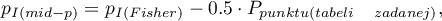
where:

$p_{I(mid-p)}$ – one-sided p-value of mid-p,

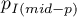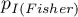$p_{I(Fisher)}$ – one-sided p-value of Fisher exact test,

and the two-sided p-value is defined as a doubled value of the smaller one-sided probability: $\begin{displaymath} p_{II(mid-p)}=2p_{I(mid-p)}, \end{displaymath}$

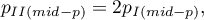
where:

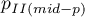$p_{II(mid-p)}$ – two-sided p-value of mid-p.

The settings window with the chi-square test and its corrections can be opened in Statistics menu → NonParametric tests→Chi-square, Fisher, OR/RR or in ''Wizard''.

¹⁾

Yates F. (1934), Contingency tables involving small numbers and the chi-square test. Journal of the Royal Statistical Society, 1,2 17-235

²⁾

Fisher R.A. (1934), Statistical methods for research workers (5th ed.). Edinburgh: Oliver and Boyd.

³⁾

Fisher R.A. (1935), The logic of inductive inference. Journal of the Royal Statistical Society, Series A, 98,39-54

⁴⁾

Lancaster H.O. (1961), Significance tests in discrete distributions. Journal of the American Statistical Association 56:223-234

⁵⁾

Anscombe F.J. (1981), Computing in Statistical Science through APL. Springer-Verlag, New York

⁶⁾

Pratt J.W. and Gibbons J.D. (1981), Concepts of Nonparametric Theory. Springer-Verlag, New York

⁷⁾

Plackett R.L. (1984), Discussion of Yates' „Tests of significance for 2×2 contingency tables”. Journal of Royal Statistical Society Series A 147:426-463

⁸⁾

Miettinen O.S. (1985), Theoretical Epidemiology: Principles of Occurrence Research in Medicine. John Wiley and Sons, New York

⁹⁾

Barnard G.A. (1989), On alleged gains in power from lower p-values. Statistics in Medicine 8:1469-1477

¹⁰⁾

Rothman K.J., Greenland S., Lash T.L. (2008), Modern Epidemiology, 3rd ed. (Lippincott Williams and Wilkins) 221-225

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

The Chi-square test corrections for small tables

Narzędzia strony