Spis treści
Analizy opisowe
Dane zebrane przez badacza w pierwszej kolejności powinny zostać opisane. W zależności od sposobu dokonywania pomiarów (od skali pomiarowej) do opisu zmiennej użyjemy różnych miar.
Skale pomiarowe
Poprawne określenie rodzaju wykonywanej analizy zależy od skali na jakiej wyrażone są zebrane dane. Wyróżniamy 3 główne skale pomiarowe:
- Skala interwałowa (przedziałowa) (ang. interval scale)
Zmienna jest wyrażona na skali interwałowej, gdy:- można ją uporządkować,
- można obliczyć o ile jeden element jest większy od drugiego i różnica tych elementów ma interpretację w świecie rzeczywistym. Zwykle określona jest jednostka miary.
Przykład: masa obiektu [kg], powierzchnia obiektu [m], czas [lata], prędkość [km/h] itp.
-
- można ją uporządkować, czyli ma znaczenie kolejność występowania elementów,
- nie da się w sensowny sposób określić różnicy ani ilorazu między dwiema wartościami.
Przykład: wykształcenie, kolejność zawodników na podium itp.
Uwaga!
Jeśli zmienna jest wyrażona na skali porządkowej, to by można było wykonać na niej w sposób prawidłowy obliczenia powinna być zapisana za pomocą liczb. Liczby te to umowne identyfikatory mówiące o kolejności elementów.
-
- nie można jej uporządkować, czyli nie istnieje wynikające z natury danego zjawiska uporządkowanie,
- nie da się w sensowny sposób określić różnicy ani ilorazu między dwiema wartościami.
Przykład: płeć, kraj zamieszkania itp.
Uwaga!
Jeśli zmienna jest wyrażona na skali nominalnej, to może być zapisana za pomocą etykiet tekstowych. Nawet jeśli wartości zmiennej nominalnej są wyrażane liczbowo, to liczby te są tylko umownymi identyfikatorami, nie można więc wykonywać na nich działań arytmetycznych, ani ich porównywać.
Przed przystąpieniem do analiz zalecane jest przyporządkowanie skali pomiarowej poszczególnym zmiennym. Takie przypisanie spowoduje, że nagłówki zmiennych zyskają odpowiadający danej skali kolor tzn. kolor zielony = skala interwałowa, kolor żółty = skala porządkowa, kolor czerwony = skala nominalna. Kolor zmiennych (a więc ich skala) będzie widoczny w arkuszu danych i na liście zmiennych w oknach analiz.
Przypisania skali do wybranej zmiennej możemy dokonać w oknie opcji zmiennych Kody/Etykiety/Format lub w menu kontekstowym na nagłówku wybranej zmiennej.
Dane ilościowe to wszelkie informacje, które można określić ilościowo, policzyć lub zmierzyć i nadać im wartość liczbową. Do danych ilościowych zaliczamy skalę interwałową i niekiedy również skalę porządkową.
Dane jakościowe mają charakter opisowy, wyrażony raczej w kategoriach językowych niż w wartościach liczbowych. Do danych jakościowych zaliczamy skalę nominalną i niekiedy również skalę porządkową.
Skala porządkowa która ma możliwych wiele zobiektywizowanych kategorii to dane ilościowe np. skala jakości życia SF-36 (od 0 do 100 punktów), ale jeśli kategorii jest tak niewiele, że można je opisać tekstem np. wykształcenie (podstawowe, średnie, wyższe), to są to dane jakościowe.
Tabele
Tabele liczności i rozkłady empiryczne
Podstawą badań statystycznych jest określenie rozkładu empirycznego tzn. zaobserwowanego w próbie rozkładu cechy. Określenie empirycznego rozkładu polega na przyporządkowaniu kolejnym wartościom przyjmowanym przez cechę częstości ich występowania. Rozkład taki można przedstawić w postaci tabeli liczności lub w postaci wykresu (histogramu). Dla małych zbiorów danych tabele liczności mogą prezentować wszystkie dane - tzw. szeregi rozdzielcze punktowe, w przypadku większych zbiorów danych tworzy się tzw. szeregi rozdzielcze przedziałowe.
Aby przedstawić rozkład danych w postaci tabeli należy wyświetlić okno Tabele liczności poprzez wybranie menu Statystyka→Analizy opisowe→Tabele liczności.
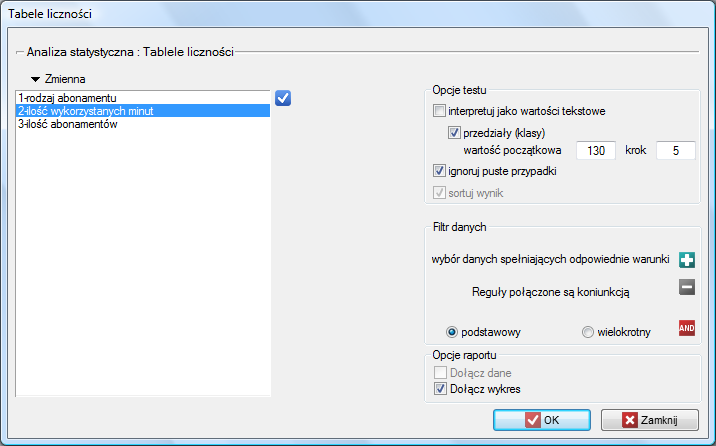
W oknie tym wybieramy zmienną do analizy oraz opcje analizy. Wybierając odpowiednie opcje zwrócony wynik możemy posortować traktując zmienne jako wartości tekstowe lub jako liczby. Jeśli występują w analizowanej kolumnie puste komórki, to mogą być wliczane do analizy bądź pomijane. Wynik dokonanej analizy znajdzie się w raporcie dołączonym do arkusza danych, dla których analiza została wykonana.
Dodatkowo, jeśli chcemy by dane zostały zobrazowane za pomocą wykresu kolumnowego lub histogramu, wówczas w oknie Tabel liczności zaznaczamy opcję Dołącz wykres.
Pewien operator telefonii komórkowej przeprowadza szereg badań dotyczących wykorzystania przez klientów liczby przyznanych w abonamencie „darmowych minut”. Klienci w każdym miesiącu mogą wykorzystać do 190 takich minut. Badanie przeprowadzono na podstawie losowej próby 200 klientów. Analizowano między innymi informacje o:
- rodzaju wykupionego abonamentu,
- liczby wykorzystanych darmowych minut,
- liczby zarejestrowanych na danego klienta abonamentów (nie dotyczy firm).
Chcemy przedstawić rozkład:
- rodzaju abonamentu,
- liczby wykorzystanych darmowych minut,
- liczby zarejestrowanych abonamentów na osoby prywatne.
Uruchamiamy okno Tabele liczności.
- Wybieramy
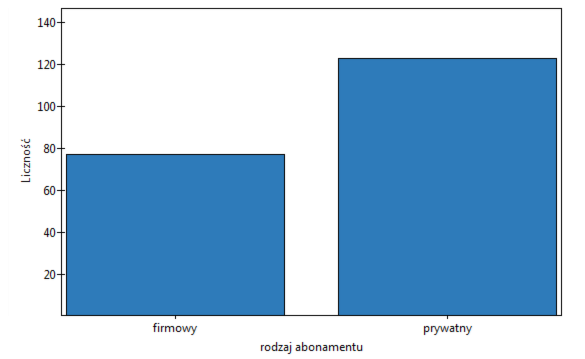
Zmiennądo analizy: „rodzaj abonamentu” i zaznaczamy opcjęInterpretuj jako wartości tekstoweorazDołącz wykres. Następnie potwierdzamy wybrane ustawienia przyciskiemOKi uzyskujemy wynik w postaci raportu:

- Wznawiamy analizę przyciskiem
 . Wybieramy
. Wybieramy Zmiennądo analizy: „liczba wykorzystanych minut” i zaznaczamy opcjęPrzedziały (klasy),wartość początkowąustawiamy np. na 130 akrokna 5. Możemy również zaznaczyć opcjęDołącz wykres. Następnie wybrane opcje potwierdzamy przyciskiemOKi uzyskujemy wynik w postaci raportu:
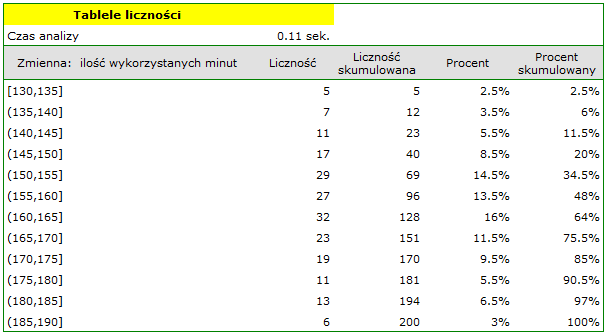
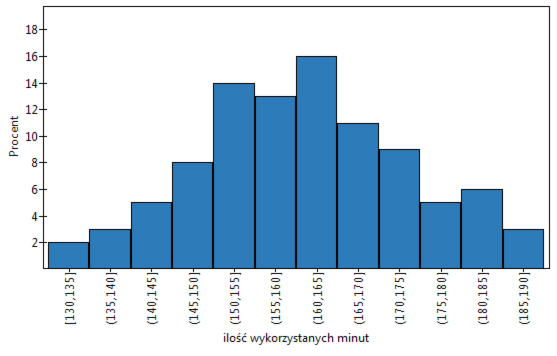
- Wznawiamy analizę przyciskiem
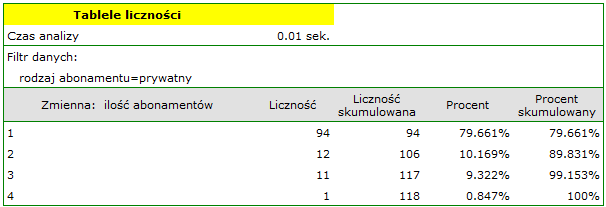
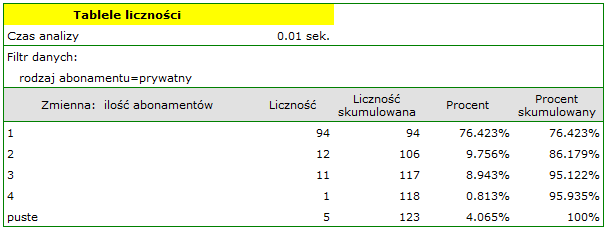
 . Ustawiamy filtr tak by analiza była wykonana wyłącznie dla osób prywatnych. Wybieramy
. Ustawiamy filtr tak by analiza była wykonana wyłącznie dla osób prywatnych. Wybieramy Zmiennądo analizy: „Liczba abonamentów”. Ponieważ zmienna ta zawiera również braki danych, uzyskany wynik może uwzględniać te braki w analizie lub nie, w zależności od wybranej opcji dotyczącej ignorowania pustych przypadków:
Przykład (plik nawozy.pqs)
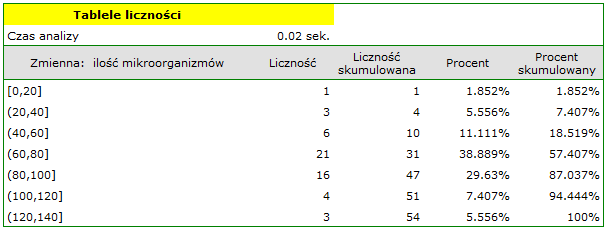
Przeprowadzono doświadczenie, w którym badano stan mikrobiologiczny gleby pod uprawą życicy trwałej zasilanej nawozami biologicznie aktywnymi. Gleby nawożono różnymi rodzajami preparatów mikrobiologicznych i nawozów a następnie wyliczono ilość mikroorganizmów występujących w 1 gramie suchej masy gleby. Chcemy znać częstość występowania promieniowców na 1 gram suchej masy gleby nawożonej azotem. Interesuje nas jak często w badanej próbie występowało od 0 do 20 promieniowców, od więcej niż 20 do 40 promieniowców, od więcej niż 40 do 60 promieniowców, itd. Zaznaczamy w arkuszu danych tylko 54 pierwsze wiersze, które odpowiadają założeniom analizy (są to promieniowce nawożone azotem) i uruchamiamy okno Tabele liczności poprzez menu Statystyka→Tabele liczności.
W oknie opcji wybieramy zmienną do analizy: Ilość mikroorganizmów, a następnie ustawiamy przedziały klasowe w ten sposób, by wartością początkową było 0 a krokiem 20. Na górze okna powinien być widoczny komunikat:
Dane ograniczone przez zaznaczenie
Potwierdzamy wybór przyciskiem OK i uzyskujemy wynik w postaci raportu:
Raport tabeli
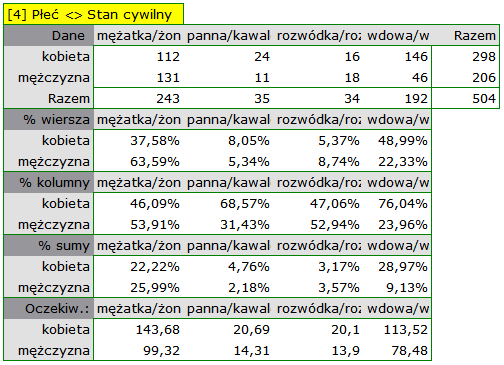
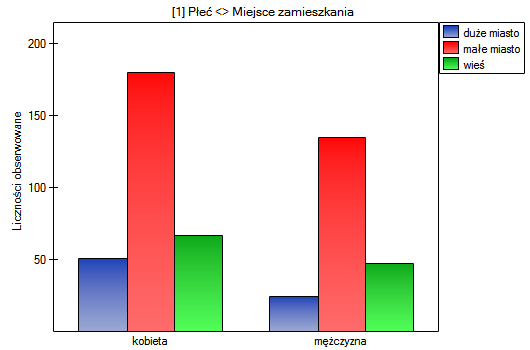
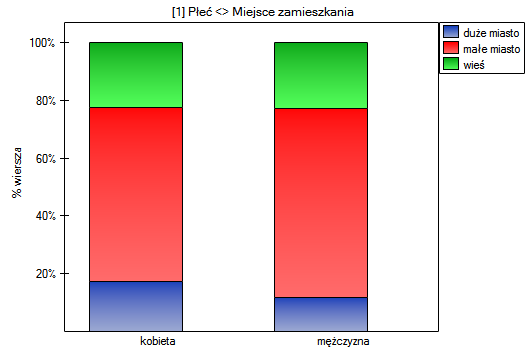
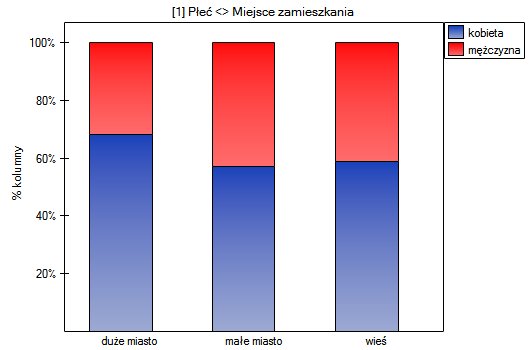
Przy pomocy raportu tabeli można przygotować jednoczesne podsumowanie bardzo wielu danych w postaci setek tabel dwudzielczych (tabel dwóch cech). Na przykład w postaci tabeli możemy przedstawić rozkład grup wiekowych według miejsca zamieszkania, wykształcenia, itd. Każda tabela jest przedstawiana w postaci liczności w poszczególnych kategoriach oraz dodatkowo można ją podsumować wyliczając procenty z wiersza, z kolumny lub z sumy całkowitej oraz wyznaczyć tabelę liczności oczekiwanych. Ponadto dla takich tabel możliwe jest automatyczne podsumowania w postaci wykresu kolumnowego.
Okno z ustawieniami opcji raportu tabel wywołujemy poprzez menu Statystyka→Analizy opisowe→Raport tabeli
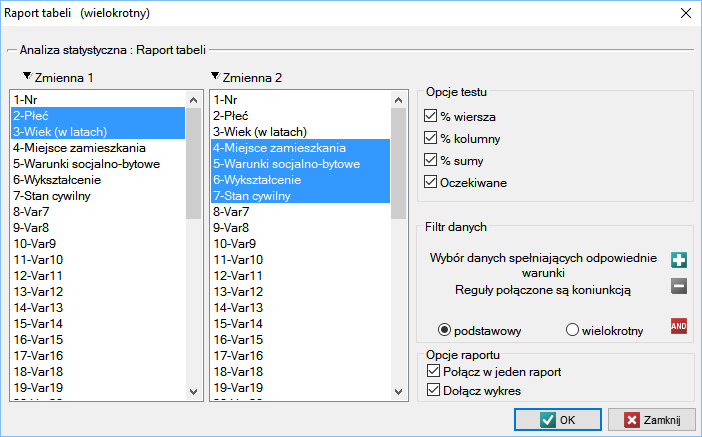
Przykład (plik Tabele.pqs)
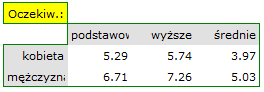
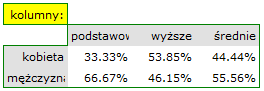
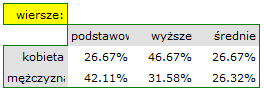
W postaci tabel należy podsumować rozkład płci według miejsca zamieszkania, warunków socjalno-bytowych, wykształcenia, stanu cywilnego oraz rozkład grup wiekowych względem tych samych cech. W rezultacie uzyskamy po 4 tabele dla każdej pary cech, czyli 8 tabel dla wszystkich par i odpowiadające im wykresy. Poniżej przedstawiono tylko zestawienie względem płci:
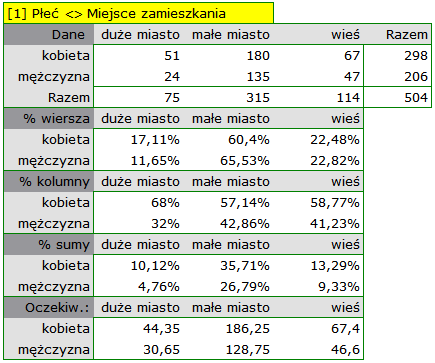
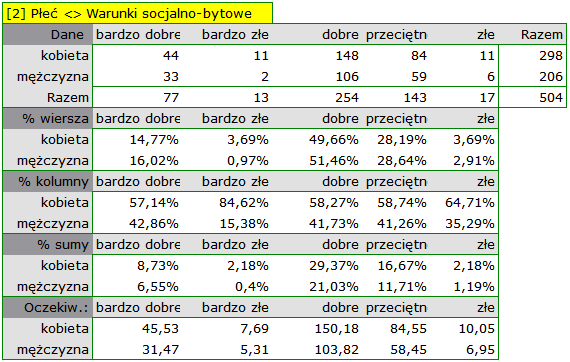
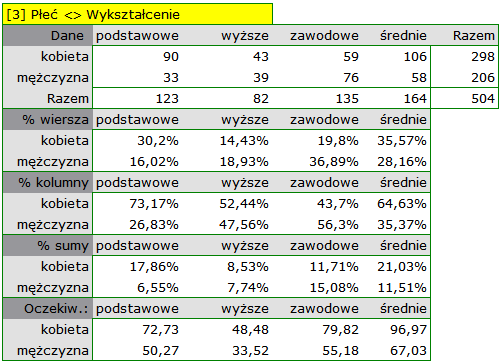
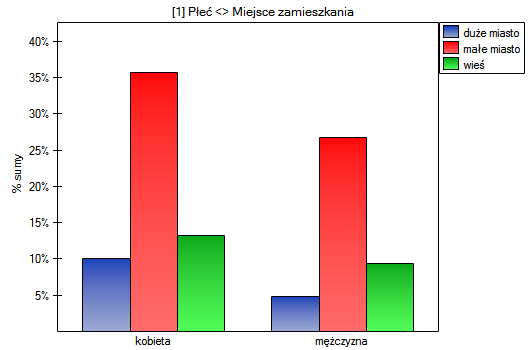
Dla rozkładu względem grup wiekowych utworzono najpierw kategorie wiekowe poprzez kody/etykiety/format.
Analizy dla tabel
Analizy dla tabel kontyngencji mogą być wyliczane na podstawie danych zebranych w tabele kontyngencji lub bezpośrednio tzn. na podstawie danych w postaci surowej. Przy czym istnieje możliwość transformacji danych z tabeli kontyngencji do postaci surowej lub odwrotnie.
Przykład (plik płeć-wykształcenie.pqs)
Rozpatrzmy próbę składającą się z 34 osób ( ). Badamy 2 cechy tych osób (
). Badamy 2 cechy tych osób ( =płeć,
=płeć,  =wykształcenie). Płeć występuje w 2 kategoriach (
=wykształcenie). Płeć występuje w 2 kategoriach ( =kobieta,
=kobieta,  =mężczyzna) wykształcenie w 3 kategoriach, (
=mężczyzna) wykształcenie w 3 kategoriach, (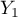 = podstawowe + zawodowe
= podstawowe + zawodowe 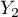 =średnie,
=średnie,  =wyższe).
=wyższe).
W przypadku danych surowych, po otwarciu okna opcji testu np. testu  dla tabel
dla tabel  , zaznaczona będzie automatycznie opcja
, zaznaczona będzie automatycznie opcja dane surowe.
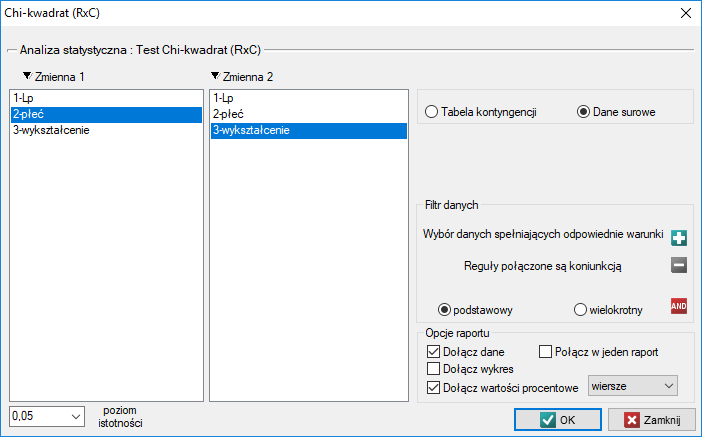
W przypadku danych zebranych w tabeli kontyngencji dobrze jest zaznaczyć te dane (wartości liczbowe bez nagłówków) przed uruchomieniem okna testu. Wówczas po otwarciu okna testu zaznaczona będzie automatycznie opcja tabela kontyngencji i dane z zaznaczenia zostaną wyświetlone.
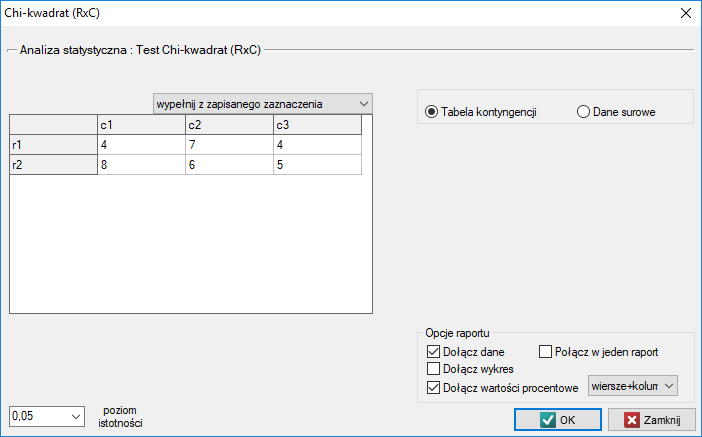
W oknie testu zawsze możemy zmienić automatycznie wykryte ustawienie dotyczące formy organizacji danych, jak też wpisywać z poziomu okna dane do tabeli kontyngencji.
Warunek Cochrana
Jest to podstawowy warunek stosowania wielu testów statystycznych opartych na tabelach kontyngencji np. testu chi-kwadrat. Warunek ten zakłada duże liczności oczekiwane. Według interpretacji Cochrana (1952)1) żadna z liczności oczekiwanych nie może być 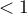 oraz nie więcej niż 20% liczności oczekiwanych może być
oraz nie więcej niż 20% liczności oczekiwanych może być 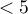 . Informacja o spełnieniu (bądź nie spełnieniu) tego warunku przez dane zebrane w tabeli może być zwrócona do raportu.
. Informacja o spełnieniu (bądź nie spełnieniu) tego warunku przez dane zebrane w tabeli może być zwrócona do raportu.
Podstawowe testy dla tabel kontyngencji:
Współczynniki dla tabel kontyngencji:
W raporcie wynikowym można również umieścić podstawowe podsumowanie tabel:
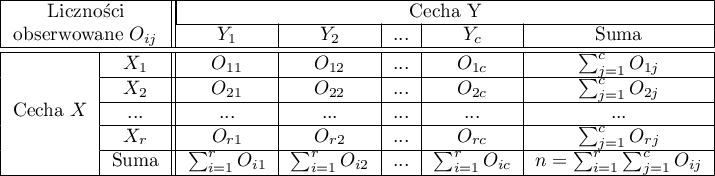
Liczności obserwowane 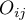 (
(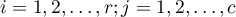 ) przedstawiają częstość występowania poszczególnych kategorii dla obu cech.
) przedstawiają częstość występowania poszczególnych kategorii dla obu cech.
By tabela taka była zwrócona przez program należy w oknie testu wybrać opcję dołącz analizowane dane.
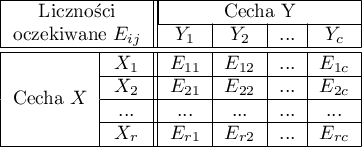
gdzie:
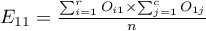 ,
, 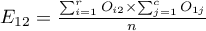 ,
, 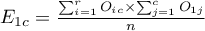
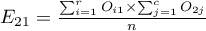 ,
, 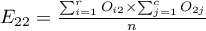 ,
, 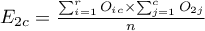
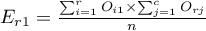 ,
, 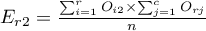 ,
, 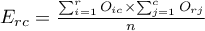 .
.
- Tabelę kontyngencji wartości procentowych wyliczanych z sumy kolumn.
- Tabelę kontyngencji wartości procentowych wyliczanych z sumy wierszy.
- Tabelę kontyngencji wartości procentowych wyliczanych z sumy całkowitej .
Statystyka opisowa
Celem stosowania metod statystyki opisowej jest podsumowanie zbioru danych poprzez pewne charakterystyki np. poprzez wartość średniej, mediany czy odchylenia standardowego, oraz wyciągnięcie pewnych podstawowych wniosków i uogólnień na temat zbioru.
Aby wyznaczyć statystyki opisowe dla danych zgromadzonych w arkuszu należy wyświetlić okno Statystyki opisowe poprzez wybranie menu Statystyka→Statystyki opisowe.
W oknie tym wybieramy zmienną do analizy oraz opcje analizy i zaznaczamy interesujące nas miary statystyk opisowych. Przy czym zaznaczać można pojedyncze statystyki lub grupy statystyk wybierając przycisk  . Dokonany wybór potwierdzamy przyciskiem
. Dokonany wybór potwierdzamy przyciskiem OK. Wynik dokonanej analizy znajdzie się w raporcie dołączonym do arkusza danych, dla których analiza została wykonana.
Dodatkowo, jeśli chcemy by dane zostały zobrazowane za pomocą wykresu ramka-wąsy, wówczas w oknie Statystyk opisowych zaznaczamy opcję Dołącz wykres.
Miary położenia
Miary tendencji centralnej
Miary tendencji centralnej są to tzw. miary przeciętne charakteryzujące średni lub typowy poziom wartości cechy.
Średnia arytmetyczna (ang. arithmetic mean) wyraża się wzorem:
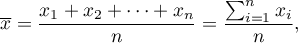
gdzie  to kolejne wartości zmiennej a
to kolejne wartości zmiennej a  - liczność próby.
- liczność próby.
Średnia arytmetyczna jest stosowana dla skali interwałowej. Dla próby przyjmuje się ją oznaczać przez 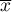 a dla populacji przez
a dla populacji przez 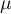 .
.
Średnia przycięta (Trimmed mean)- wyznaczana jest jako średnia arytmetyczna obliczona po usunięciu z próbki zadanego procentu najmniejszych i największych pomiarów np. gdy obcinamy 5% pomiarów, to oznacza, że obcinamy 2.5% największych i 2.5% najmniejszych wartości. Przy czym, gdy uzyskana na podstawie przeliczań liczba pomiarów przeznaczonych do usunięcia nie będzie liczbą całkowitą, wówczas jest ona zaokrąglana w dół do najbliższej całkowitej.
Średnia Winsora (Winsor mean) - wyznaczana jest jako średnia arytmetyczna obliczona po zastąpieniu odpowiedniego odsetka skrajnych pomiarów wartością najmniejszą i największą jaka pozostała zmniejszonym zbiorze wartości. Jeśli zdecydujemy się na obliczanie średniej Winsora przycinając np. 5% pomiarów, to wówczas te odrzucone 5% zostanie zastąpione wartością najmniejszą i największą wyznaczoną z pozostałych 95% pomiarów. Podobnie jak dla średniej przycinanej, gdy na podstawie przeliczenia procentu wartości przeznaczonych do zamiany na liczbę pomiarów przeznaczonych do zamiany nie uzyskamy liczby całkowitej, wówczas zaokrąglamy w dół do najbliższej całkowitej.
Średnia geometryczna (ang. geometric mean) wyraża się wzorem:
![LaTeX \begin{displaymath}
\overline{x}_G=\sqrt[n]{x_1x_2...x_n}=\sqrt[n]{\prod_{i=1}^n x_i}.
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img011017a5d163d0e6305611f865ade072.png) Średnia ta jest stosowana dla skali interwałowej, gdy zmienna ma rozkład logarytmiczno-normalny (logarytm zmiennej ma rozkład normalny).
Średnia ta jest stosowana dla skali interwałowej, gdy zmienna ma rozkład logarytmiczno-normalny (logarytm zmiennej ma rozkład normalny).
Średnia harmoniczna (ang. harmonic mean) wyraża się wzorem:
 Średnia ta jest stosowana dla skali interwałowej.
Średnia ta jest stosowana dla skali interwałowej.
W uporządkowanym zbiorze danych mediana jest wartością dzielącą ten zbiór na dwie równe części. Połowa wszystkich obserwacji znajduje się poniżej, a połowa powyżej mediany.
![LaTeX \begin{pspicture}(0,0)(10,10.6)
\pscoil[coilaspect=0, coilarm=.1cm, linewidth=0.5pt, coilwidth=.5cm, coilheight=1]{-}(0,4)
\rput(0,4.2){min}
\rput(0,-.2){max}
\psline(-0.35,2)(.35,2)
\rput(1.2,2){mediana}
\rput(-0.6,2.8){50$\%$}
\rput(-0.6,1.2){50$\%$}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img826223981ace04d4f37d432b7063428a.png)
Mediana może być stosowana w skali interwałowej oraz porządkowej.
Moda  jest to wartość, która występuje najczęściej wśród uzyskanych pomiarów. Moda może być stosowana w każdej skali pomiarowej.
jest to wartość, która występuje najczęściej wśród uzyskanych pomiarów. Moda może być stosowana w każdej skali pomiarowej.
Inne miary położenia
kwartyle (ang. quartiles), decyle (ang. deciles), centyle (ang. centiles)
![LaTeX \begin{pspicture}(0,-.2)(4,4.4)
\pscoil[coilaspect=0, coilarm=.1cm, linewidth=0.5pt, coilwidth=.5cm, coilheight=1]{-}(0,4)
\rput(0,4.2){max}
\rput(0,-.2){min}
\psline(-0.35,3)(.35,3)
\psline(-0.35,2)(.35,2)
\psline(-0.35,1)(.35,1)
\rput(2.9,3){$C_{75}$ = kwartyl górny = $Q_3$}
\rput(2.4,2){$C_{50}$ = mediana = $Q_2$}
\rput(2.9,1){$C_{25}$ = kwartyl dolny = $Q_1$}
\rput(1,3.5){25$\%$}
\rput(1,2.5){25$\%$}
\rput(1,1.5){25$\%$}
\rput(1,.5){25$\%$}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img95cc67a481e2d6314660a8aa6c567235.png)
Kwartyle (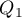 ,
, 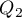 ,
, 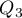 ) dzielą uporządkowany szereg na 4 równe części, decyle (
) dzielą uporządkowany szereg na 4 równe części, decyle (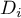 ,
, 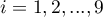 ) na 10 równych części a centyle (percentyle:
) na 10 równych części a centyle (percentyle: 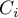 ,
, 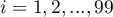 ) na 100 równych części. Drugi kwartyl, piąty decyl i pięćdziesiąty centyl są równe medianie. Miary te mogą być stosowane w skali interwałowej oraz porządkowej.
) na 100 równych części. Drugi kwartyl, piąty decyl i pięćdziesiąty centyl są równe medianie. Miary te mogą być stosowane w skali interwałowej oraz porządkowej.
Miary rozproszenia
Znajomość miar tendencji centralnej nie wystarcza do scharakteryzowania struktury zbiorowości statystycznej. Badana grupa może charakteryzować się różnym stopniem zmienności w zakresie badanej cechy. Potrzebne są zatem formuły pozwalające wyznaczyć wartości, które charakteryzują rozrzut danych.
Miary rozproszenia są liczone tylko dla skali interwałowej, ponieważ bazują one na odległościach między punktami.
Rozstęp (ang. range) wyraża się wzorem:
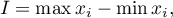
gdzie  to wartości badanej zmiennej
to wartości badanej zmiennej
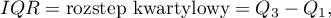
gdzie 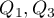 to dolny i górny kwartyl.
to dolny i górny kwartyl.
Rozstępy dla skali percentylowej (decylowej, centylowej). Rozstępy miedzy percentylami to jedna z miar rozproszenia i określa procent wszystkich obserwacji, których wartość znajduje się pomiędzy wybranymi percentylami.
Wariancja (ang. variance) - mierzy stopień rozproszenia pomiarów wokół średniej arytmetycznej
- wariancja z próby:
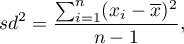
gdzie  to kolejne wartości zmiennej a
to kolejne wartości zmiennej a 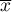 to średnia arytmetyczna tych wartości,
to średnia arytmetyczna tych wartości,  - liczność próby.
- liczność próby.
- wariancja z populacji:
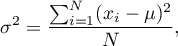
gdzie  to kolejne wartości zmiennej a
to kolejne wartości zmiennej a 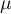 to średnia arytmetyczna tych wartości,
to średnia arytmetyczna tych wartości, 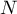 - liczność populacji.
- liczność populacji.
Wariancja jest zawsze dodatnia, ale nie jest wyrażona w tych samych jednostkach co wyniki pomiarów.
Odchylenie standardowe (ang. standard deviation)  mierzy stopień rozproszenia pomiarów wokół średniej arytmetycznej.
mierzy stopień rozproszenia pomiarów wokół średniej arytmetycznej.
- odchylenie standardowe z próby:
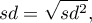
- odchylenie standardowe z populacji:
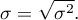
Im wyższa wartość odchylenia standardowego lub wariancji, tym bardziej zróżnicowana grupa pod względem badanej cechy.
Uwaga! Odchylenie standardowe z próby jest pewnym przybliżeniem (estymatorem) odchylenia standardowego z populacji. Populacyjna wartość odchylenia standardowego mieści się w pewnym przedziale zawierającym odchylenie standardowe z próby. Przedział ten nazywany jest przedziałem ufności (confidence interval) dla odchylenia standardowego.
Współczynnik zmienności (ang. coefficient of variation)
Współczynnik zmienności podobnie jak odchylenie standardowe pozwala na ocenę stopnia jednorodności badanej zbiorowości. Wyraża się wzorem:
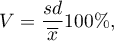
gdzie 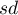 to odchylenie standardowe,
to odchylenie standardowe, 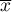 to średnia arytmetyczna.
to średnia arytmetyczna.
Jest to wielkość niemianowana. Pozwala on na ocenę zróżnicowania kilku zbiorowości pod względem tej samej cechy oraz tej samej zbiorowości pod względem kilku różnych cech (wyrażonych w różnych jednostkach). Przyjmuje się, że jeżeli współczynnik 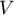 nie przekracza 10\%, to cechy wykazują zróżnicowanie statystycznie nieistotne.
nie przekracza 10\%, to cechy wykazują zróżnicowanie statystycznie nieistotne.
Błędy standardowe (ang. standard errors) - nie są miarami rozproszenia wyników pomiarowych, lecz określają stopień dokładności z jaką możemy określić wartości parametrów populacji na podstawie wyznaczenia ich estymatorów dla próby.
Błąd średniej arytmetycznej (ang. standard error of the mean) wyraża się następującym wzorem:
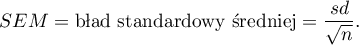
Uwaga! Na podstawie błędu standardowego estymatora z próby można określić przedział ufności dla parametru populacji.
Inne atrybuty rozkładu
Skośność inaczej współczynnik asymetrii (ang. skewness)
Jest to miara, która mówi o tym jak bardzo rozkład danych różni się od rozkładu symetrycznego. Im wartość współczynnika asymetrii jest bliższa zeru, tym bardziej symetrycznie wokół średniej rozkładają się dane. Zwykle wartość tego współczynnika zawiera się w przedziale [-1, 1], chociaż może w przypadku szczególnie dużej asymetrii znaleźć się poza tym przedziałem. Wartości dodatnie świadczą o występowaniu skośności prawostronnej (o dłuższym prawym „ogonie”) wartości ujemne zaś o skośności lewostronnej (o dłuższym lewym „ogonie”). Skośność wyraża się wzorem:
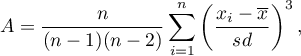
gdzie:
 – kolejne wartości zmiennej,
– kolejne wartości zmiennej,
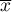 ,
, 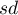 – odpowiednio średnia arytmetyczna i odchylenie standardowe
– odpowiednio średnia arytmetyczna i odchylenie standardowe  ,
,
 – liczność próby.
– liczność próby.
![LaTeX \begin{tabular}{cc}
\begin{pspicture}(0,-.7)(7,3.6)
\rput(2.5,3.3){skośność prawostronna}
\rput(2.8,2.8){$A>0$}
\psline{->}(0,0)(0,3)
\psline{->}(0,0)(6.3,0)
\psbezier{-}(.2,.2)(.5,.2)(.7,2.3)(1.3,2.5)
\psbezier{-}(1.3,2.5)(2,2.5)(3,.2)(5.3,.2)
\psline[linestyle=dotted]{-}(2.2,0)(2.2,1.7)
\rput(2.55,-.3){Med.}
\psline[linestyle=dotted]{-}(1.3,0)(1.3,2.5)
\rput(1.3,-.3){Moda}
\psline[linestyle=dotted]{-}(3.4,0)(3.4,.7)
\rput(3.5,-.3){$\overline{X}$}
\rput{90}(-.4,2.7){częstość}
\rput(6.1,-.3){x}
\end{pspicture}
&
\begin{pspicture}(0,-.7)(7,3.6)
\rput(2.5,3.3){skośność lewostronna}
\rput(2.2,2.8){$A<0$}
\psline{->}(0,0)(0,3)
\psline{->}(0,0)(6.3,0)
\psbezier{-}(.2,.2)(2.1,.2)(2.8,2.5)(3.7,2.5)
\psbezier{-}(3.7,2.5)(4.2,2.5)(4.8,.2)(5.5,.2)
\psline[linestyle=dotted]{-}(2.85,0)(2.85,1.75)
\rput(2.7,-.3){Med.}
\psline[linestyle=dotted]{-}(3.7,0)(3.7,2.5)
\rput(3.9,-.3){Moda}
\psline[linestyle=dotted]{-}(1.7,0)(1.7,.7)
\rput(1.7,-.3){$\overline{X}$}
\rput{90}(-.4,2.7){częstość}
\rput(6.1,-.3){x}
\end{pspicture}
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img0e1a8fde93ad1f126fa614ca317cb07a.png)
Kurtoza inaczej współczynnik koncentracji (ang. kurtosis)
Jest to miara, która mówi o tym jak bardzo rozrzut danych wokół średniej jest zbliżony do rozrzutu tych danych w rozkładzie normalnym. Im wartość kurtozy jest większa od zera, tym badany rozkład jest bardziej smukły niż rozkład normalny a im wartość kurtozy jest mniejsza od zera, tym badany rozkład jest bardziej spłaszczony niż rozkład normalny. Kurtoza wyraża się wzorem:
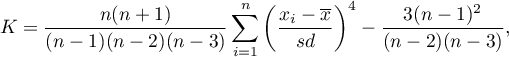
gdzie:
 – kolejne wartości zmiennej,
– kolejne wartości zmiennej,
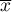 ,
, 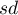 – odpowiednio średnia arytmetyczna i odchylenie standardowe
– odpowiednio średnia arytmetyczna i odchylenie standardowe  ,
,
 – liczność próby.
– liczność próby.
![LaTeX \begin{pspicture}(0,-.8)(6.5,3.4)
\rput(4.0,.7){$K_1<0$}
\rput(4.5,2.5){$K_2>0$}
\psline{->}(0,0)(0,3)
\psline{->}(0,0)(7,0)
\psbezier[linestyle=dashed]{-}(.2,.2)(2.2,.8)(2.3,1.4)(3.2,1.5)
\psbezier[linestyle=dashed]{-}(3.2,1.5)(4.1,1.4)(4.2,.8)(6.2,.2)
\psbezier{-}(.4,.2)(2.4,.6)(2.5,3.0)(3.2,3.1)
\psbezier{-}(3.2,3.1)(3.9,3.0)(4.0,.6)(6.0,.2)
\psline[linestyle=dotted]{-}(3.2,0)(3.2,3.1)
\rput(3.2,-.3){$\overline{X}$}
\rput{90}(-.4,2.7){częstość}
\rput(6.8,-.3){x}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img1db9eb4b65eaf100bd5055c2b3a9f66c.png)
Przykład (plik nawozy.pqs)
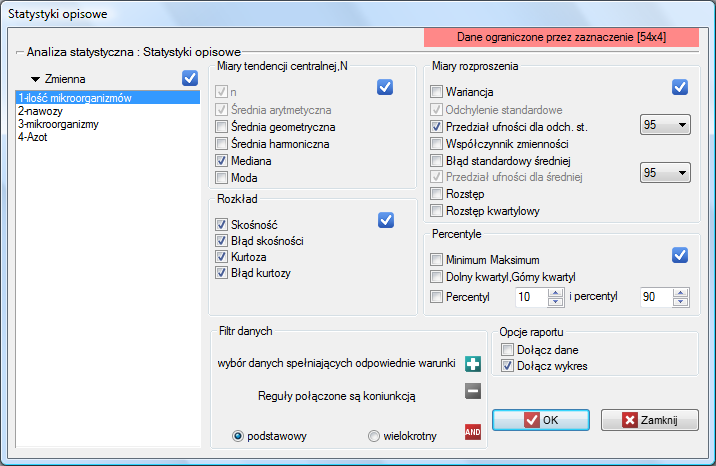
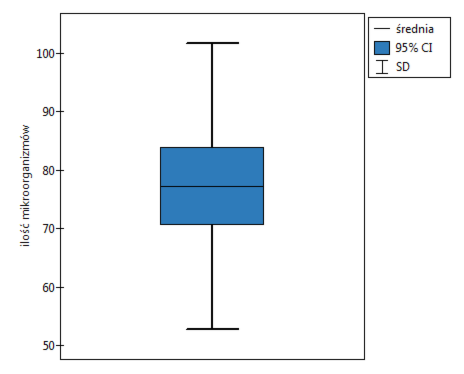
W doświadczeniu dotyczącym nawożenia gleby różnymi rodzajami preparatów mikrobiologicznych i nawozów wyliczono ilość mikroorganizmów występujących w 1 gramie suchej masy gleby. Chcemy wyznaczyć statystyki opisowe ilości promieniowców dla próbki nawożonej azotem i zobrazować uzyskane wyniki za pomocą wykresu ramka-wąsy. Zaznaczamy w arkuszu danych tylko 54 pierwsze wiersze, które odpowiadają założeniom analizy (są to promieniowce nawożone azotem) i uruchamiamy okno Statystyki opisowe poprzez menu Statystyka→Statystyki opisowe.
W oknie opcji testu statystyk opisowych wybieramy zmienną do analizy: Ilość mikroorganizmów, a następnie procedury jakie chcemy wykonać (np. średnią arytmetyczną wraz z przedziałem ufności, medianę, odchylenie standardowe wraz z przedziałem ufności oraz informacje o skośności i kurtozie rozkładu wraz z błędami). Na górze okna powinien być widoczny komunikat:
Dane ograniczone przez zaznaczenie
By w raporcie znalazł się również wykres, zaznaczamy opcję Dołącz wykres i wybieramy interesujący nas rodzaj wykresu ramka-wąsy. Potwierdzamy wybór przyciskiem OK i uzyskujemy wynik w postaci raportu:

 a druga
a druga  kategorii przedstawiono poniżej).
kategorii przedstawiono poniżej).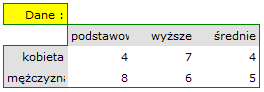
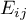 .
.