Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Baza Wiedzy » statpqpl » Analizy opisowe » Tabele » Analizy dla tabel
Pasek boczny
pl:statpqpl:aopisowapl:tabliczpl:analizytbpl
Analizy dla tabel
Analizy dla tabel kontyngencji mogą być wyliczane na podstawie danych zebranych w tabele kontyngencji lub bezpośrednio tzn. na podstawie danych w postaci surowej. Przy czym istnieje możliwość transformacji danych z tabeli kontyngencji do postaci surowej lub odwrotnie.
Przykład (plik płeć-wykształcenie.pqs)
Rozpatrzmy próbę składającą się z 34 osób ( ). Badamy 2 cechy tych osób (
). Badamy 2 cechy tych osób ( =płeć,
=płeć,  =wykształcenie). Płeć występuje w 2 kategoriach (
=wykształcenie). Płeć występuje w 2 kategoriach ( =kobieta,
=kobieta,  =mężczyzna) wykształcenie w 3 kategoriach, (
=mężczyzna) wykształcenie w 3 kategoriach, (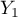 = podstawowe + zawodowe
= podstawowe + zawodowe 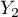 =średnie,
=średnie, 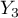 =wyższe).
=wyższe).
W przypadku danych surowych, po otwarciu okna opcji testu np. testu  dla tabel
dla tabel  , zaznaczona będzie automatycznie opcja
, zaznaczona będzie automatycznie opcja dane surowe.
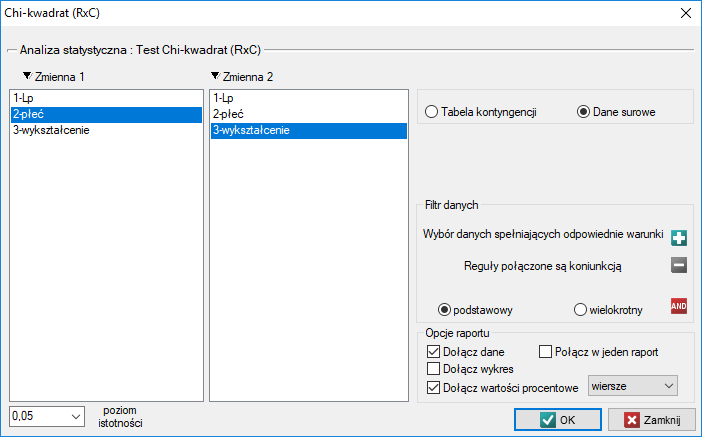
W przypadku danych zebranych w tabeli kontyngencji dobrze jest zaznaczyć te dane (wartości liczbowe bez nagłówków) przed uruchomieniem okna testu. Wówczas po otwarciu okna testu zaznaczona będzie automatycznie opcja tabela kontyngencji i dane z zaznaczenia zostaną wyświetlone.
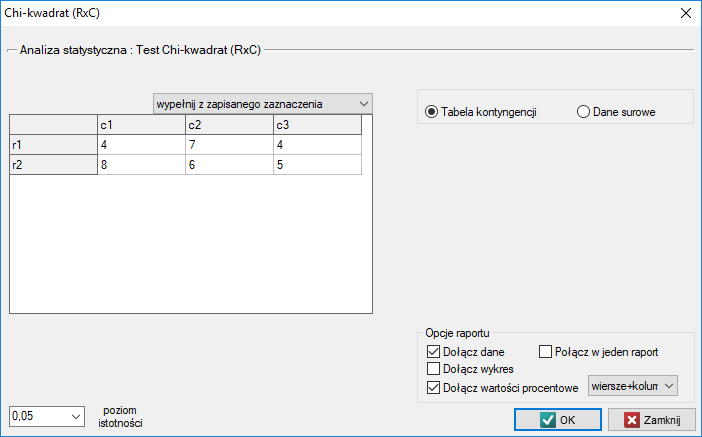
W oknie testu zawsze możemy zmienić automatycznie wykryte ustawienie dotyczące formy organizacji danych, jak też wpisywać z poziomu okna dane do tabeli kontyngencji.
Warunek Cochrana
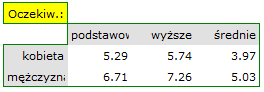
Jest to podstawowy warunek stosowania wielu testów statystycznych opartych na tabelach kontyngencji np. testu chi-kwadrat. Warunek ten zakłada duże liczności oczekiwane. Według interpretacji Cochrana (1952)1) żadna z liczności oczekiwanych nie może być 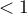 oraz nie więcej niż 20% liczności oczekiwanych może być
oraz nie więcej niż 20% liczności oczekiwanych może być 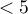 . Informacja o spełnieniu (bądź nie spełnieniu) tego warunku przez dane zebrane w tabeli może być zwrócona do raportu.
. Informacja o spełnieniu (bądź nie spełnieniu) tego warunku przez dane zebrane w tabeli może być zwrócona do raportu.
Podstawowe testy dla tabel kontyngencji:
Współczynniki dla tabel kontyngencji:
W raporcie wynikowym można również umieścić podstawowe podsumowanie tabel:
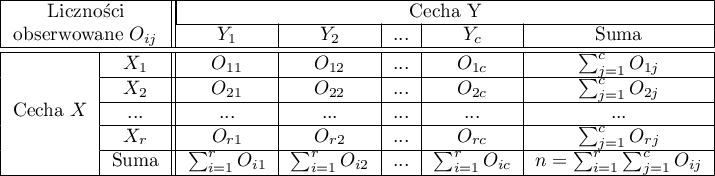
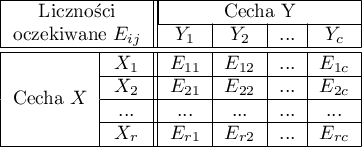
Liczności obserwowane 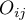 (
(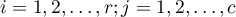 ) przedstawiają częstość występowania poszczególnych kategorii dla obu cech.
) przedstawiają częstość występowania poszczególnych kategorii dla obu cech.
By tabela taka była zwrócona przez program należy w oknie testu wybrać opcję dołącz analizowane dane.
gdzie:
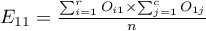 ,
, 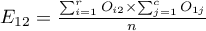 ,
, 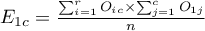
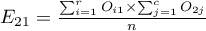 ,
, 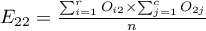 ,
, 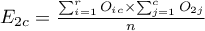
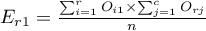 ,
, 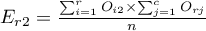 ,
, 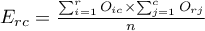 .
.
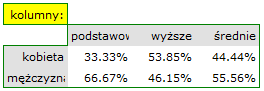
- Tabelę kontyngencji wartości procentowych wyliczanych z sumy kolumn.
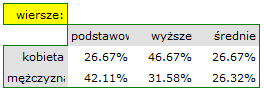
- Tabelę kontyngencji wartości procentowych wyliczanych z sumy wierszy.
- Tabelę kontyngencji wartości procentowych wyliczanych z sumy całkowitej .
1)
Cochran W.G. (1952), The chi-square goodness-of-fit test. Annals of Mathematical Statistics, 23, 315-345
pl/statpqpl/aopisowapl/tabliczpl/analizytbpl.txt · ostatnio zmienione: 2022/02/10 22:29 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

 czyli dane w postaci tabeli kontyngencji. Tabela taka przedstawia rozkład obserwacji dla kilku cech (kilku zmiennych). Tabelę dla 2 cech (
czyli dane w postaci tabeli kontyngencji. Tabela taka przedstawia rozkład obserwacji dla kilku cech (kilku zmiennych). Tabelę dla 2 cech ( a druga
a druga  kategorii przedstawiono poniżej).
kategorii przedstawiono poniżej).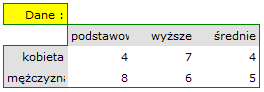
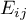 .
.