Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:korelpl:nparpl:kontrpl
Współczynniki tabel kontyngencji i ich istotność statystyczna
Współczynniki kontyngencji są wyliczane dla danych w postaci surowej lub danych zebranych w tabelę kontyngencji.
Okno z ustawieniami opcji miar zależności dla tabel wywołujemy poprzez menu Statystyka→Testy nieparametryczne →Chi-kwadrat, Fisher, OR/RR→Współczynniki korelacji… lub poprzez ''Kreator''.
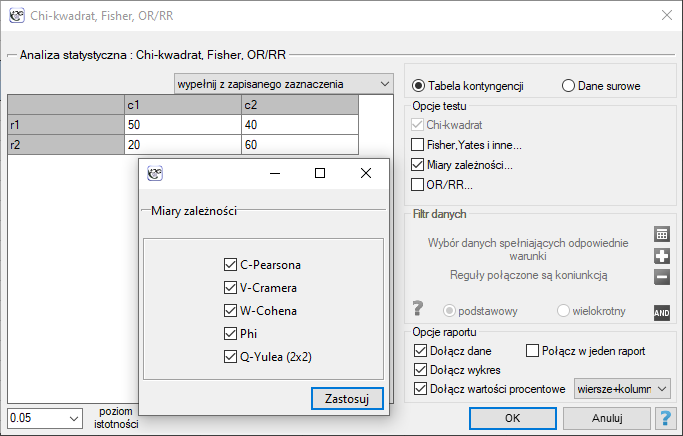
Współczynnik kontyngencji Q-Yulea
Współczynnik kontyngencji  -Yulea (Yule's Q contingency coefficient), Yule (1900)1), jest miarą zależności, która może być wyznaczana dla tabel kontyngencji
-Yulea (Yule's Q contingency coefficient), Yule (1900)1), jest miarą zależności, która może być wyznaczana dla tabel kontyngencji 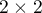
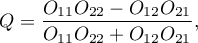
gdzie:
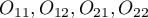 - liczności obserwowane w tabeli kontyngencji.
- liczności obserwowane w tabeli kontyngencji.
Oryginalnie wartość współczynnika  mieści się w przedziale
mieści się w przedziale 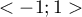 . Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa
. Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa  1 lub +1, tym siła badanego związku jest większa (ze względu na błędy w interpretacji ujemnej wartości współczynnika, wyniki tego współczynnika w programie PQStat przedstawiane są wówczas również jako wartość bezwzględna). Wadą tego współczynnika jest to, iż jest mało odporny na małe liczności obserwowane (gdy jakaś z liczności obserwowanych wynosi 0, to współczynnik może błędnie wskazywać całkowitą zależność cech).
1 lub +1, tym siła badanego związku jest większa (ze względu na błędy w interpretacji ujemnej wartości współczynnika, wyniki tego współczynnika w programie PQStat przedstawiane są wówczas również jako wartość bezwzględna). Wadą tego współczynnika jest to, iż jest mało odporny na małe liczności obserwowane (gdy jakaś z liczności obserwowanych wynosi 0, to współczynnik może błędnie wskazywać całkowitą zależność cech).
Istotność statystyczną wyznaczonego współczynnika kontyngencji  -Yulea określamy testem
-Yulea określamy testem  .
.
Hipotezy:
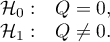
Statystyka testowa ma postać:
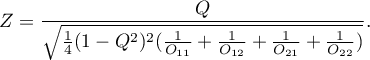
Statystyka testowa ma asymptotycznie (dla dużych liczności  ) rozkład normalny.
) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Współczynnik kontyngencji 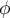 (ang. phi contingency coefficient) jest miarą zależności polecaną szczególnie dla tabel kontyngencji
(ang. phi contingency coefficient) jest miarą zależności polecaną szczególnie dla tabel kontyngencji 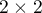 , chociaż możliwą do wyznaczenia dla dowolnych tabel.
, chociaż możliwą do wyznaczenia dla dowolnych tabel.
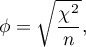
Wartość współczynnika 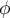 mieści się w przedziale
mieści się w przedziale 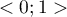 . Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa wartości 1 tym większa.
. Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa wartości 1 tym większa.
Współczynnik kontyngencji 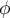 uznaje się za istotny statystycznie jeśli wartość
uznaje się za istotny statystycznie jeśli wartość  wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności
wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności  .
.
Współczynnik kontyngencji 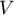 -Cramera
-Cramera
Współczynnik kontyngencji 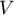 -Cramera (ang. Cramer's V contingency coefficient), Cramer (1946)2), jest rozszerzeniem współczynnika
-Cramera (ang. Cramer's V contingency coefficient), Cramer (1946)2), jest rozszerzeniem współczynnika 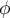 na tabele kontyngencji
na tabele kontyngencji 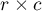 .
.
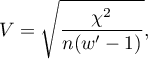
gdzie:
wartość - wartość statystyki testu chi-kwadrat,
- wartość statystyki testu chi-kwadrat,
 - całkowita liczność w tabeli kontyngencji,
- całkowita liczność w tabeli kontyngencji,
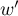 - jest mniejszą z dwóch wartości
- jest mniejszą z dwóch wartości  i
i  .
.
Wartość współczynnika 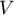 mieści się w przedziale
mieści się w przedziale 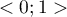 . Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa +1, tym siła badanego związku jest większa. Wartość współczynnika
. Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa +1, tym siła badanego związku jest większa. Wartość współczynnika 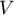 zależy również od wielkości tabeli, stąd nie powinno się stosować tego współczynnika do porównywania tabel kontyngencji o różnych wielkościach.
zależy również od wielkości tabeli, stąd nie powinno się stosować tego współczynnika do porównywania tabel kontyngencji o różnych wielkościach.
Współczynnik kontyngencji 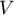 uznaje się za istotny statystycznie jeśli wartość
uznaje się za istotny statystycznie jeśli wartość  wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności
wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności  .
.
Współczynnik kontyngencji  -Cohena
-Cohena
Współczynnik kontyngencji  -Cohena (ang. Cohen's w contingency coefficient), Cohen (1988)3), jest modyfikacją współczynnika
-Cohena (ang. Cohen's w contingency coefficient), Cohen (1988)3), jest modyfikacją współczynnika 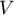 -Cramera i jest możliwy do wyliczenia dla tabel
-Cramera i jest możliwy do wyliczenia dla tabel 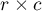 .
.
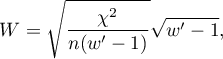
gdzie:
wartość - wartość statystyki testu chi-kwadrat,
- wartość statystyki testu chi-kwadrat,
 - całkowita liczność w tabeli kontyngencji,
- całkowita liczność w tabeli kontyngencji,
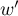 - jest mniejszą z dwóch wartości
- jest mniejszą z dwóch wartości  i
i  .
.
Wartość współczynnika  mieści się w przedziale
mieści się w przedziale 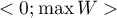 , gdzie
, gdzie  (dla tabel, w których co najmniej jedna zmienna zawiera tylko dwie kategorie wartość współczynnika
(dla tabel, w których co najmniej jedna zmienna zawiera tylko dwie kategorie wartość współczynnika  mieści się w przedziale
mieści się w przedziale 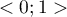 ). Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa maksymalnej wartości, tym siła badanego związku jest większa. Wartość współczynnika
). Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa maksymalnej wartości, tym siła badanego związku jest większa. Wartość współczynnika  zależy od wielkości tabeli, stąd nie powinno się stosować tego współczynnika do porównywania tabel kontyngencji o różnych wielkościach.
zależy od wielkości tabeli, stąd nie powinno się stosować tego współczynnika do porównywania tabel kontyngencji o różnych wielkościach.
Współczynnik kontyngencji  uznaje się za istotny statystycznie jeśli wartość
uznaje się za istotny statystycznie jeśli wartość  wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności
wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności  .
.
Współczynnik kontyngencji C Pearsona
Współczynnik kontyngencji  -Pearsona (ang. Pearson's C contingency coefficient) jest miarą zależności wyznaczaną dla tabel kontyngencji
-Pearsona (ang. Pearson's C contingency coefficient) jest miarą zależności wyznaczaną dla tabel kontyngencji 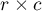
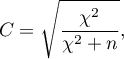
Wartość współczynnika  mieści się w przedziale
mieści się w przedziale 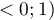 . Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im dalsza od 0, tym siła badanego związku jest większa. Ponieważ wartość współczynnika
. Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im dalsza od 0, tym siła badanego związku jest większa. Ponieważ wartość współczynnika  zależy również od wielkości tabeli (im większa tabela, tym wartość
zależy również od wielkości tabeli (im większa tabela, tym wartość  może być bliższa 1), dlatego wyznacza się górną granicę jaką dla danej wielkości tabeli współczynnik
może być bliższa 1), dlatego wyznacza się górną granicę jaką dla danej wielkości tabeli współczynnik  może osiągnąć:
może osiągnąć:
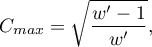
gdzie:
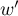 - jest mniejszą z dwóch wartości
- jest mniejszą z dwóch wartości  i
i  .
.
Niewygodną konsekwencją uzależnienia wartości  od wielkości tabeli jest brak możliwości porównywania wartości współczynnika
od wielkości tabeli jest brak możliwości porównywania wartości współczynnika  wyznaczonego dla różnych wielkości tabel kontyngencji. Nieco lepszą miarą w takim przypadku jest dostosowana do wielkości tabeli wielkość współczynnika kontyngencji
wyznaczonego dla różnych wielkości tabel kontyngencji. Nieco lepszą miarą w takim przypadku jest dostosowana do wielkości tabeli wielkość współczynnika kontyngencji 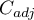
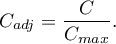
Współczynnik kontyngencji  uznaje się za istotny statystycznie jeśli wartość
uznaje się za istotny statystycznie jeśli wartość  wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności
wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności  .
.
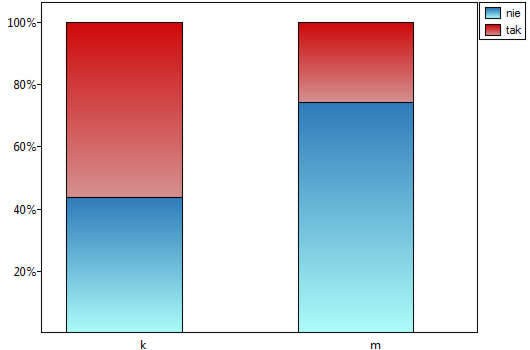
Przykład (plik płeć-egzamin.pqs)
Rozpatrzmy próbę składającą się z 170 osób (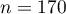 ), dla których badamy 2 cechy (
), dla których badamy 2 cechy ( =płeć,
=płeć,  =zdawalność egzaminu). Każda z tych cech występuje w dwóch kategoriach (
=zdawalność egzaminu). Każda z tych cech występuje w dwóch kategoriach ( =k,
=k,  =m,
=m, 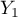 =tak,
=tak, 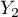 =nie). Na podstawie tej próby chcielibyśmy się dowiedzieć, czy w badanej populacji istnieje zależność pomiędzy płcią a zdawalnością egzaminu. Rozkład danych przedstawia tabeli kontyngencji:}
=nie). Na podstawie tej próby chcielibyśmy się dowiedzieć, czy w badanej populacji istnieje zależność pomiędzy płcią a zdawalnością egzaminu. Rozkład danych przedstawia tabeli kontyngencji:}
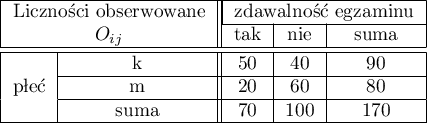
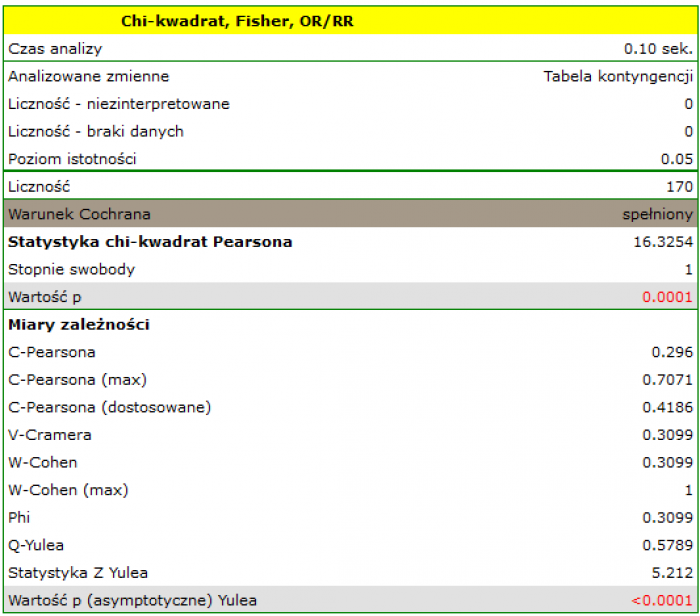
Wartość statystyki testowej wynosi 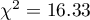 a wyznaczona dla niej wartość
a wyznaczona dla niej wartość 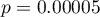 . Uzyskany wynik wskazuje na istnienie zależności statystycznej pomiędzy płcią a zdawalnością egzaminu w badanej populacji.
. Uzyskany wynik wskazuje na istnienie zależności statystycznej pomiędzy płcią a zdawalnością egzaminu w badanej populacji.
Wartość współczynników opartych o test  , a zatem siła związku między badanymi cechami to:
, a zatem siła związku między badanymi cechami to:
Współczynnik kontyngencji 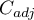 -Pearsona = 0.42.
-Pearsona = 0.42.
Współczynnik kontyngencji 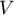 -Cramera =
-Cramera = 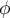 =
=  -Cohena =0.31
-Cohena =0.31
Współczynnik kontyngencji  -Yulea=0.58, a wartość
-Yulea=0.58, a wartość  wykonanego testu
wykonanego testu  podobnie jak poziom istotności testu
podobnie jak poziom istotności testu  wskazuje na istotność statystyczną badanego związku.
wskazuje na istotność statystyczną badanego związku.
1)
Yule G. (1900), On the association of the attributes in statistics: With illustrations from the material ofthe childhood society, and c. Philosophical Transactions of the Royal Society, Series A, 194,257-3 19
2)
Cramkr H. (1946), Mathematical models of statistics. Princeton, NJ: Princeton University Press
3)
Cohen J. (1988), Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates, Hillsdale, New Jersey
statpqpl/korelpl/nparpl/kontrpl.txt · ostatnio zmienione: 2022/01/23 21:26 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

