Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:aopisowapl:tabliczpl
Tabele
Tabele liczności i rozkłady empiryczne
Podstawą badań statystycznych jest określenie rozkładu empirycznego tzn. zaobserwowanego w próbie rozkładu cechy. Określenie empirycznego rozkładu polega na przyporządkowaniu kolejnym wartościom przyjmowanym przez cechę częstości ich występowania. Rozkład taki można przedstawić w postaci tabeli liczności lub w postaci wykresu (histogramu). Dla małych zbiorów danych tabele liczności mogą prezentować wszystkie dane - tzw. szeregi rozdzielcze punktowe, w przypadku większych zbiorów danych tworzy się tzw. szeregi rozdzielcze przedziałowe.
Aby przedstawić rozkład danych w postaci tabeli należy wyświetlić okno Tabele liczności poprzez wybranie menu Statystyka→Analizy opisowe→Tabele liczności.
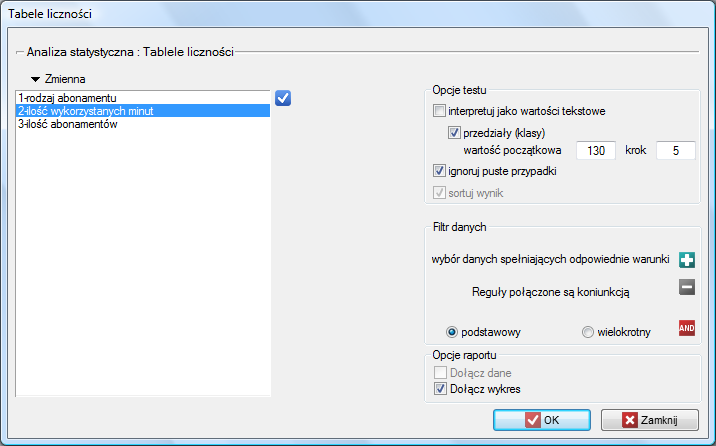
W oknie tym wybieramy zmienną do analizy oraz opcje analizy. Wybierając odpowiednie opcje zwrócony wynik możemy posortować traktując zmienne jako wartości tekstowe lub jako liczby. Jeśli występują w analizowanej kolumnie puste komórki, to mogą być wliczane do analizy bądź pomijane. Wynik dokonanej analizy znajdzie się w raporcie dołączonym do arkusza danych, dla których analiza została wykonana.
Dodatkowo, jeśli chcemy by dane zostały zobrazowane za pomocą wykresu kolumnowego lub histogramu, wówczas w oknie Tabel liczności zaznaczamy opcję Dołącz wykres.
Pewien operator telefonii komórkowej przeprowadza szereg badań dotyczących wykorzystania przez klientów liczby przyznanych w abonamencie „darmowych minut”. Klienci w każdym miesiącu mogą wykorzystać do 190 takich minut. Badanie przeprowadzono na podstawie losowej próby 200 klientów. Analizowano między innymi informacje o:
- rodzaju wykupionego abonamentu,
- liczby wykorzystanych darmowych minut,
- liczby zarejestrowanych na danego klienta abonamentów (nie dotyczy firm).
Chcemy przedstawić rozkład:
- rodzaju abonamentu,
- liczby wykorzystanych darmowych minut,
- liczby zarejestrowanych abonamentów na osoby prywatne.
Uruchamiamy okno Tabele liczności.
- Wybieramy
Zmiennądo analizy: „rodzaj abonamentu” i zaznaczamy opcjęInterpretuj jako wartości tekstoweorazDołącz wykres. Następnie potwierdzamy wybrane ustawienia przyciskiemOKi uzyskujemy wynik w postaci raportu:

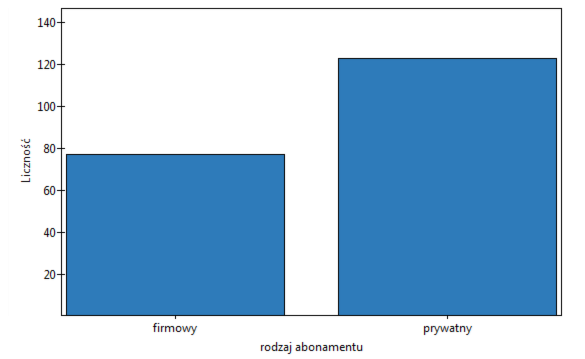
- Wznawiamy analizę przyciskiem
 . Wybieramy
. Wybieramy Zmiennądo analizy: „liczba wykorzystanych minut” i zaznaczamy opcjęPrzedziały (klasy),wartość początkowąustawiamy np. na 130 akrokna 5. Możemy również zaznaczyć opcjęDołącz wykres. Następnie wybrane opcje potwierdzamy przyciskiemOKi uzyskujemy wynik w postaci raportu:
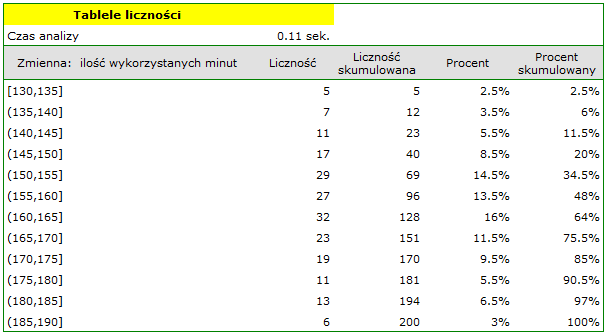
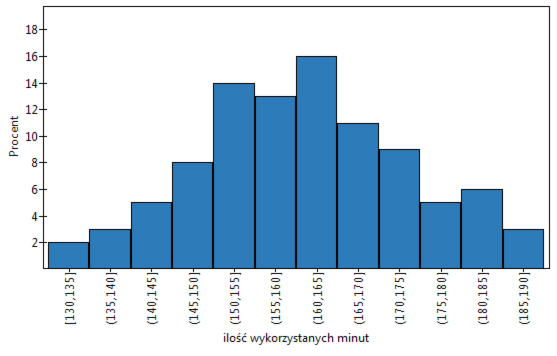
- Wznawiamy analizę przyciskiem
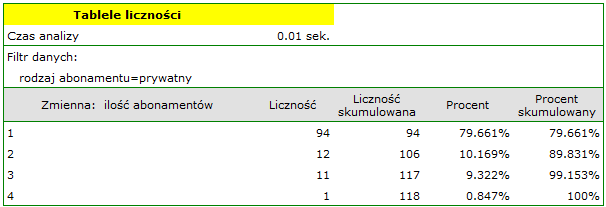
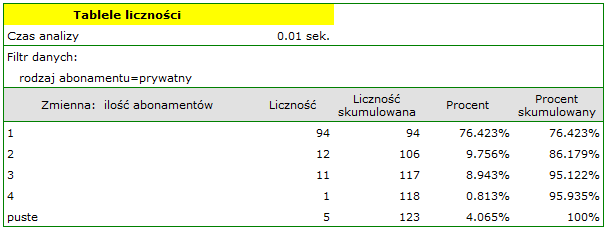
 . Ustawiamy filtr tak by analiza była wykonana wyłącznie dla osób prywatnych. Wybieramy
. Ustawiamy filtr tak by analiza była wykonana wyłącznie dla osób prywatnych. Wybieramy Zmiennądo analizy: „Liczba abonamentów”. Ponieważ zmienna ta zawiera również braki danych, uzyskany wynik może uwzględniać te braki w analizie lub nie, w zależności od wybranej opcji dotyczącej ignorowania pustych przypadków:
Przykład (plik nawozy.pqs)
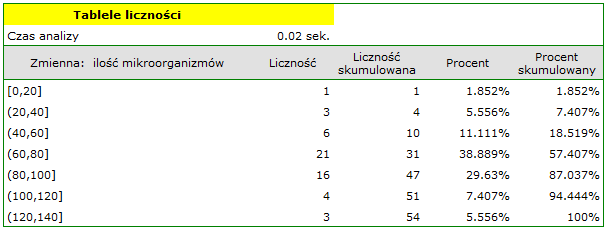
Przeprowadzono doświadczenie, w którym badano stan mikrobiologiczny gleby pod uprawą życicy trwałej zasilanej nawozami biologicznie aktywnymi. Gleby nawożono różnymi rodzajami preparatów mikrobiologicznych i nawozów a następnie wyliczono ilość mikroorganizmów występujących w 1 gramie suchej masy gleby. Chcemy znać częstość występowania promieniowców na 1 gram suchej masy gleby nawożonej azotem. Interesuje nas jak często w badanej próbie występowało od 0 do 20 promieniowców, od więcej niż 20 do 40 promieniowców, od więcej niż 40 do 60 promieniowców, itd. Zaznaczamy w arkuszu danych tylko 54 pierwsze wiersze, które odpowiadają założeniom analizy (są to promieniowce nawożone azotem) i uruchamiamy okno Tabele liczności poprzez menu Statystyka→Tabele liczności.
W oknie opcji wybieramy zmienną do analizy: Ilość mikroorganizmów, a następnie ustawiamy przedziały klasowe w ten sposób, by wartością początkową było 0 a krokiem 20. Na górze okna powinien być widoczny komunikat:
Dane ograniczone przez zaznaczenie
Potwierdzamy wybór przyciskiem OK i uzyskujemy wynik w postaci raportu:
2022/01/23 17:48
· admin
Raport tabeli
Przy pomocy raportu tabeli można przygotować jednoczesne podsumowanie bardzo wielu danych w postaci setek tabel dwudzielczych (tabel dwóch cech). Na przykład w postaci tabeli możemy przedstawić rozkład grup wiekowych według miejsca zamieszkania, wykształcenia, itd. Każda tabela jest przedstawiana w postaci liczności w poszczególnych kategoriach oraz dodatkowo można ją podsumować wyliczając procenty z wiersza, z kolumny lub z sumy całkowitej oraz wyznaczyć tabelę liczności oczekiwanych. Ponadto dla takich tabel możliwe jest automatyczne podsumowania w postaci wykresu kolumnowego.
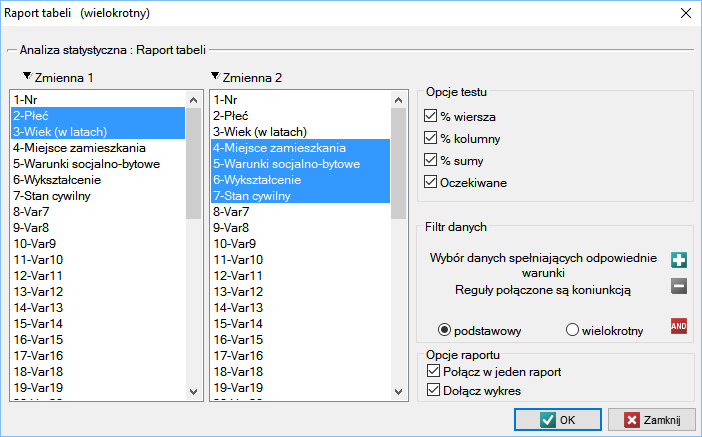
Okno z ustawieniami opcji raportu tabel wywołujemy poprzez menu Statystyka→Analizy opisowe→Raport tabeli
Przykład (plik Tabele.pqs)
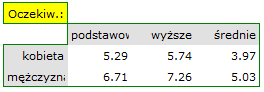
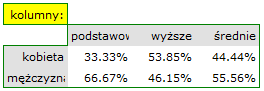
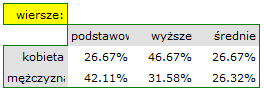
W postaci tabel należy podsumować rozkład płci według miejsca zamieszkania, warunków socjalno-bytowych, wykształcenia, stanu cywilnego oraz rozkład grup wiekowych względem tych samych cech. W rezultacie uzyskamy po 4 tabele dla każdej pary cech, czyli 8 tabel dla wszystkich par i odpowiadające im wykresy. Poniżej przedstawiono tylko zestawienie względem płci:
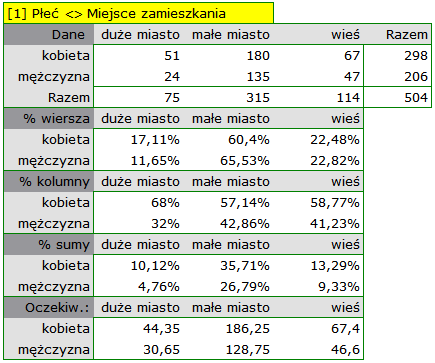
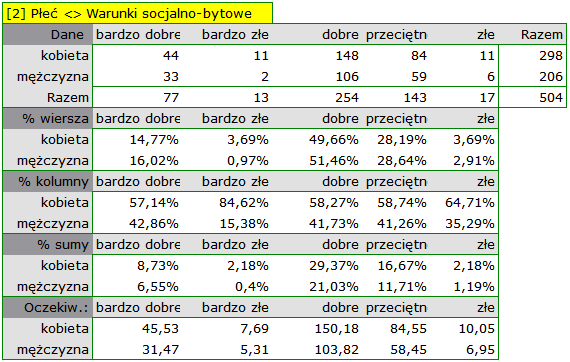
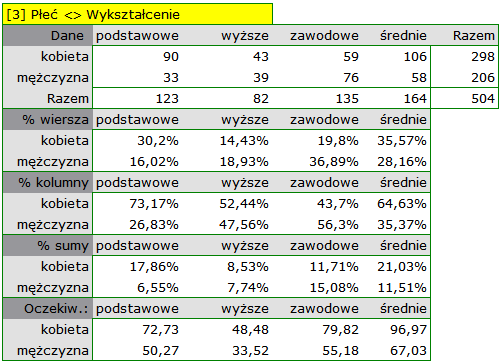
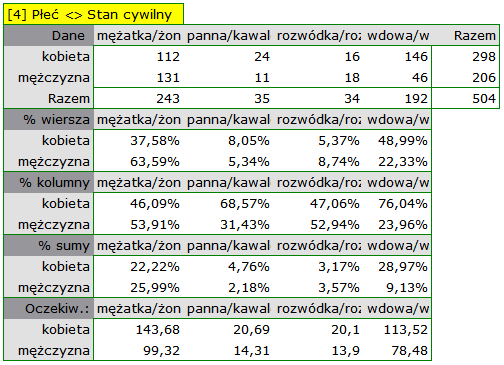
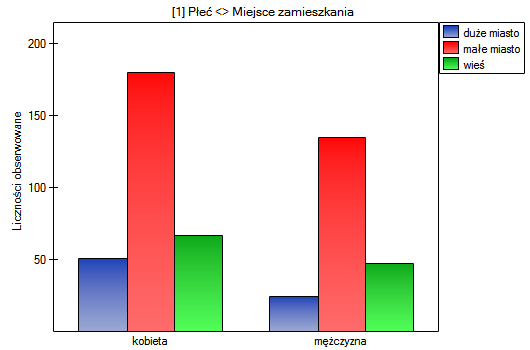
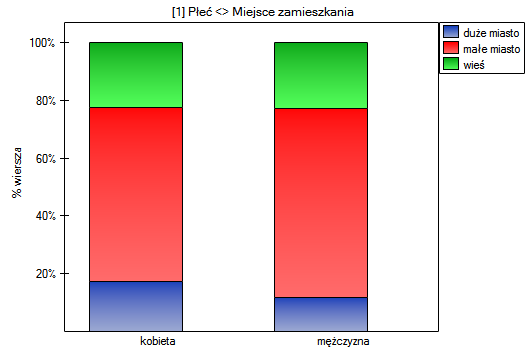
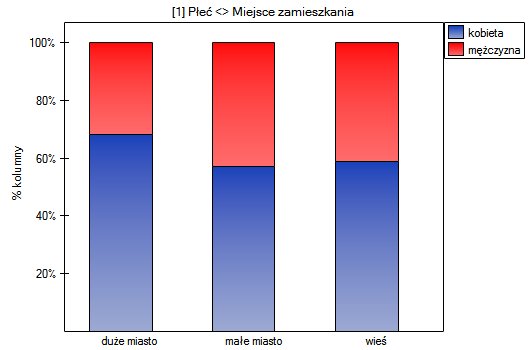
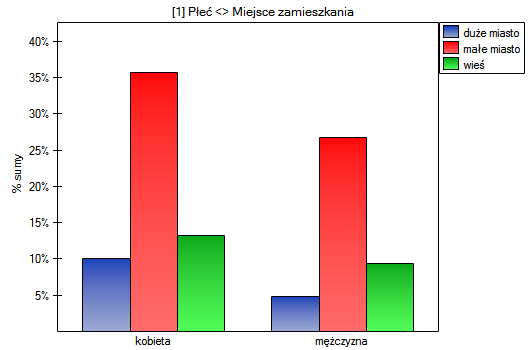
Dla rozkładu względem grup wiekowych utworzono najpierw kategorie wiekowe poprzez kody/etykiety/format.
2022/01/23 17:49
· admin
Analizy dla tabel
Analizy dla tabel kontyngencji mogą być wyliczane na podstawie danych zebranych w tabele kontyngencji lub bezpośrednio tzn. na podstawie danych w postaci surowej. Przy czym istnieje możliwość transformacji danych z tabeli kontyngencji do postaci surowej lub odwrotnie.
Przykład (plik płeć-wykształcenie.pqs)
Rozpatrzmy próbę składającą się z 34 osób ( ). Badamy 2 cechy tych osób (
). Badamy 2 cechy tych osób ( =płeć,
=płeć,  =wykształcenie). Płeć występuje w 2 kategoriach (
=wykształcenie). Płeć występuje w 2 kategoriach ( =kobieta,
=kobieta,  =mężczyzna) wykształcenie w 3 kategoriach, (
=mężczyzna) wykształcenie w 3 kategoriach, (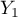 = podstawowe + zawodowe
= podstawowe + zawodowe 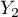 =średnie,
=średnie, 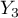 =wyższe).
=wyższe).
W przypadku danych surowych, po otwarciu okna opcji testu np. testu  dla tabel
dla tabel  , zaznaczona będzie automatycznie opcja
, zaznaczona będzie automatycznie opcja dane surowe.
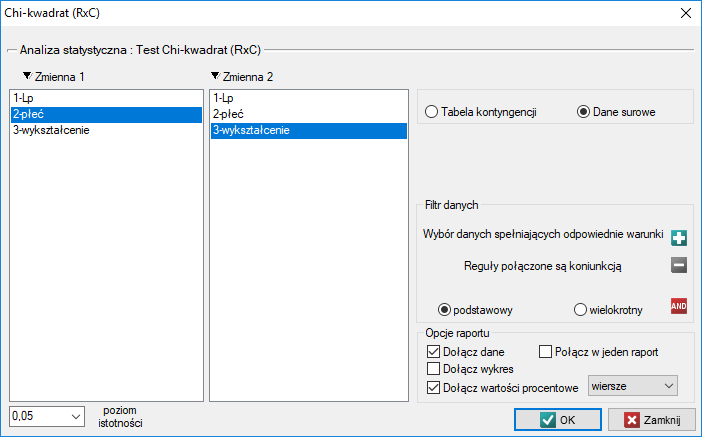
W przypadku danych zebranych w tabeli kontyngencji dobrze jest zaznaczyć te dane (wartości liczbowe bez nagłówków) przed uruchomieniem okna testu. Wówczas po otwarciu okna testu zaznaczona będzie automatycznie opcja tabela kontyngencji i dane z zaznaczenia zostaną wyświetlone.
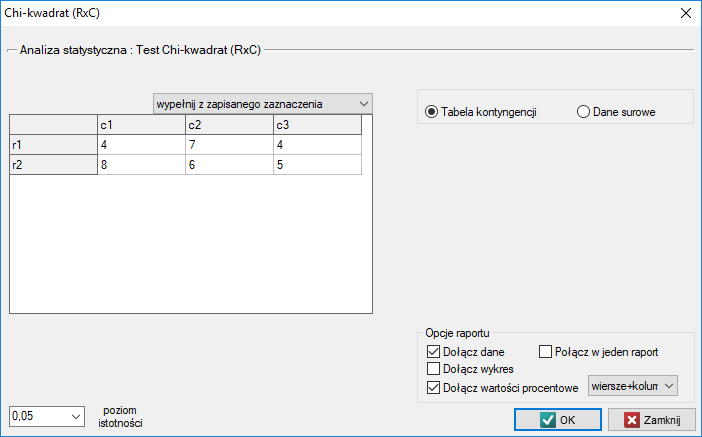
W oknie testu zawsze możemy zmienić automatycznie wykryte ustawienie dotyczące formy organizacji danych, jak też wpisywać z poziomu okna dane do tabeli kontyngencji.
Warunek Cochrana
Jest to podstawowy warunek stosowania wielu testów statystycznych opartych na tabelach kontyngencji np. testu chi-kwadrat. Warunek ten zakłada duże liczności oczekiwane. Według interpretacji Cochrana (1952)1) żadna z liczności oczekiwanych nie może być 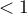 oraz nie więcej niż 20% liczności oczekiwanych może być
oraz nie więcej niż 20% liczności oczekiwanych może być 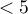 . Informacja o spełnieniu (bądź nie spełnieniu) tego warunku przez dane zebrane w tabeli może być zwrócona do raportu.
. Informacja o spełnieniu (bądź nie spełnieniu) tego warunku przez dane zebrane w tabeli może być zwrócona do raportu.
Podstawowe testy dla tabel kontyngencji:
Współczynniki dla tabel kontyngencji:
W raporcie wynikowym można również umieścić podstawowe podsumowanie tabel:
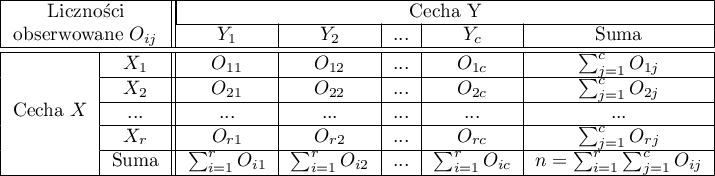
Liczności obserwowane 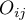 (
(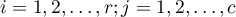 ) przedstawiają częstość występowania poszczególnych kategorii dla obu cech.
) przedstawiają częstość występowania poszczególnych kategorii dla obu cech.
By tabela taka była zwrócona przez program należy w oknie testu wybrać opcję dołącz analizowane dane.
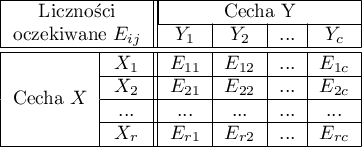
gdzie:
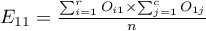 ,
, 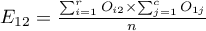 ,
, 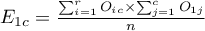
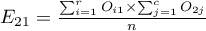 ,
, 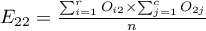 ,
, 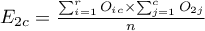
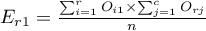 ,
, 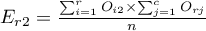 ,
, 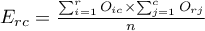 .
.
- Tabelę kontyngencji wartości procentowych wyliczanych z sumy kolumn.
- Tabelę kontyngencji wartości procentowych wyliczanych z sumy wierszy.
- Tabelę kontyngencji wartości procentowych wyliczanych z sumy całkowitej .
2022/01/23 17:49
· admin
1)
Cochran W.G. (1952), The chi-square goodness-of-fit test. Annals of Mathematical Statistics, 23, 315-345
statpqpl/aopisowapl/tabliczpl.txt · ostatnio zmienione: 2022/01/23 19:57 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

 czyli dane w postaci tabeli kontyngencji. Tabela taka przedstawia rozkład obserwacji dla kilku cech (kilku zmiennych). Tabelę dla 2 cech (
czyli dane w postaci tabeli kontyngencji. Tabela taka przedstawia rozkład obserwacji dla kilku cech (kilku zmiennych). Tabelę dla 2 cech ( a druga
a druga  kategorii przedstawiono poniżej).
kategorii przedstawiono poniżej).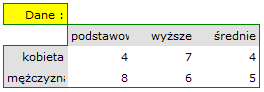
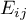 .
.