Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:korelpl:nparpl:kendrpl
Istotność współczynnika korelacji tau Kendalla
Test do sprawdzania istotności współczynnika korelacji tau Kendalla
Test do sprawdzania istotności współczynnika korelacji  Kendalla (ang. Test of significance for Kendall's tau correlation coefficient) służy do weryfikacji hipotezy o braku zależności monotonicznej pomiędzy badanymi cechami populacji i opiera się na współczynniku korelacji Kendalla wyliczonym dla próby. Im wartość wspołczynnika tau (
Kendalla (ang. Test of significance for Kendall's tau correlation coefficient) służy do weryfikacji hipotezy o braku zależności monotonicznej pomiędzy badanymi cechami populacji i opiera się na współczynniku korelacji Kendalla wyliczonym dla próby. Im wartość wspołczynnika tau ( ) jest bliższa 0, tym słabszą zależnością monotoniczną związane są badane cechy.
) jest bliższa 0, tym słabszą zależnością monotoniczną związane są badane cechy.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej.
Hipotezy:
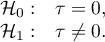
Statystyka testowa ma postać:
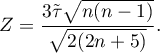 Statystyka testowa ma asymptotycznie (dla dużych liczności) rozkład normalny.
Statystyka testowa ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji zależności monotonicznej Kendalla wywołujemy poprzez menu Statystyka→Testy nieparametryczne→zależność monotoniczna (tau-Kendalla) lub poprzez ''Kreator''.
Przykład c.d. (plik LDL tygodnie.pqs)
Hipotezy:

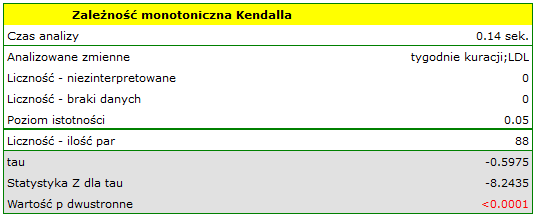
Porównując wartość  <0.0001 z poziomem istotności
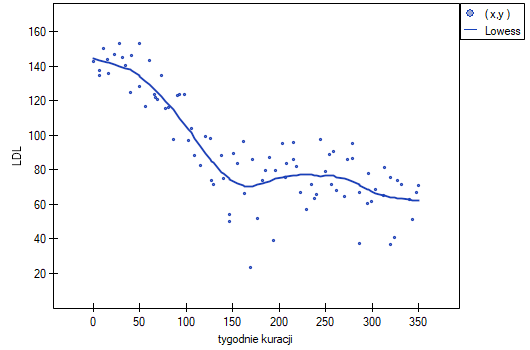
<0.0001 z poziomem istotności  stwierdzamy, że istnieje ważna statystycznie monotoniczna zależność pomiędzy czasem kuracji a poziomem LDL. Zależność ta jest początkowo malejąca, a po 150 tygodniach zaczyna się stabilizować. Współczynnik korelacji monotonicznej Kendalla, a zatem siła związku monotonicznego dla tej zależności jest dość wysoki i wynosi
stwierdzamy, że istnieje ważna statystycznie monotoniczna zależność pomiędzy czasem kuracji a poziomem LDL. Zależność ta jest początkowo malejąca, a po 150 tygodniach zaczyna się stabilizować. Współczynnik korelacji monotonicznej Kendalla, a zatem siła związku monotonicznego dla tej zależności jest dość wysoki i wynosi  =-0.5975. Wykres wyrysowano dopasowując krzywą poprzez lokalne techniki wygładzania liniowego typu LOWESS.
=-0.5975. Wykres wyrysowano dopasowując krzywą poprzez lokalne techniki wygładzania liniowego typu LOWESS.
statpqpl/korelpl/nparpl/kendrpl.txt · ostatnio zmienione: 2022/01/23 21:07 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

