Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:korelpl:nparpl:wsppl
Współczynniki korelacji monotonicznej
Zależność monotoniczna może być opisywana jako monotoniczny wzrost lub monotoniczny spadek. Związek pomiędzy 2 cechami przedstawia monotoniczny wzrost jeżeli wzrostowi jednej cechy towarzyszy wzrost drugiej cechy. Związek pomiędzy 2 cechami przedstawia monotoniczny spadek jeżeli wzrostowi jednej cechy towarzyszy spadek drugiej cechy.
Współczynnik korelacji rangowej Spearmana 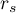 (ang. Spearman's rank-order correlation coefficient) jest wykorzystywany do badania siły związku monotonicznego pomiędzy cechami
(ang. Spearman's rank-order correlation coefficient) jest wykorzystywany do badania siły związku monotonicznego pomiędzy cechami  i
i  . Wyznacza się go dla skali porządkowej lub interwałowej.
. Wyznacza się go dla skali porządkowej lub interwałowej.
Wartość współczynnika korelacji rangowej Spearmana wylicza się według wzoru:
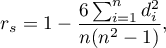
Wzór ten ulega pewniej modyfikacji gdy występują rangi wiązane:
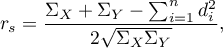
gdzie:
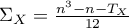 ,
, 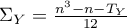 ,
,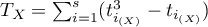 ,
, 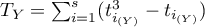 ,
, - liczba przypadków wchodzących w skład rangi wiązanej.
- liczba przypadków wchodzących w skład rangi wiązanej.
Poprawka na rangi wiązane powinna być stosowana, gdy rangi wiązane występują. Gdy nie ma rang wiązanych poprawka redukuje się i sprowadza wzór do postaci opisanej wcześniejszym równaniem.
Uwaga!
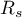 oznacza współczynnik korelacji rangowej Spearmana populacji, natomiast
oznacza współczynnik korelacji rangowej Spearmana populacji, natomiast 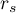 w próbie.
w próbie.
Wartość 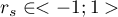 interpretujemy w następujący sposób:
interpretujemy w następujący sposób:
 oznacza silną dodatnią zależność monotoniczną (rosnącą), tj. wzrostowi zmiennej niezależnej odpowiada wzrost zmiennej zależnej;
oznacza silną dodatnią zależność monotoniczną (rosnącą), tj. wzrostowi zmiennej niezależnej odpowiada wzrost zmiennej zależnej;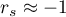 oznacza silną ujemną zależność monotoniczną (malejącą), tj. wzrostowi zmiennej niezależnej odpowiada spadek zmiennej zależnej;
oznacza silną ujemną zależność monotoniczną (malejącą), tj. wzrostowi zmiennej niezależnej odpowiada spadek zmiennej zależnej;- gdy współczynnik korelacji rangowej Spearmana przyjmuje wartość równą lub bardzo bliską zeru, wówczas nie istnieje monotoniczna zależność między badanymi parametrami (ale może istnieć związek niemonotoniczny np. sinusoidalny).
Współczynnik korelacji tau Kendalla  (ang. Kendall's tau correlation coefficient, Kendall (1938)1)) jest wykorzystywany do badania siły związku monotonicznego pomiędzy cechami. Wyznacza się go dla skali porządkowej lub interwałowej.
(ang. Kendall's tau correlation coefficient, Kendall (1938)1)) jest wykorzystywany do badania siły związku monotonicznego pomiędzy cechami. Wyznacza się go dla skali porządkowej lub interwałowej.
Wartość współczynnika korelacji tau Kendalla  wylicza się według wzoru:
wylicza się według wzoru:
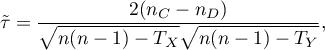
gdzie:
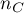 - liczbapar obserwacji, dla których wartości rang dla cechy
- liczbapar obserwacji, dla których wartości rang dla cechy  jak i dla cechy
jak i dla cechy  zmieniają się w tym samym kierunku (liczba par zgodnych),
zmieniają się w tym samym kierunku (liczba par zgodnych),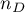 - liczba par obserwacji, dla których wartości rang dla cechy
- liczba par obserwacji, dla których wartości rang dla cechy  zmieniają się w innym kierunku niż dla cechy
zmieniają się w innym kierunku niż dla cechy  (liczba par niezgodnych),
(liczba par niezgodnych),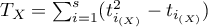 ,
, 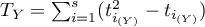 ,
, - liczba przypadków wchodzących w skład rangi wiązanej.
- liczba przypadków wchodzących w skład rangi wiązanej.
Wzór na współczynnik  zawiera poprawkę na rangi wiązane. Poprawka ta powinna być stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka nie jest wyliczana gdyż wówczas
zawiera poprawkę na rangi wiązane. Poprawka ta powinna być stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka nie jest wyliczana gdyż wówczas 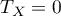 i
i 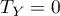 ) .
) .
Uwaga!
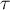 oznacza współczynnik korelacji Kendalla w populacji, natomiast
oznacza współczynnik korelacji Kendalla w populacji, natomiast  w próbie.
w próbie.
Wartość  interpretujemy w następujący sposób:
interpretujemy w następujący sposób:
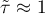 oznacza silną „zgodność” uporządkowania rang (zależność monotoniczną rosnącą), tj. wzrostowi zmiennej niezależnej odpowiada wzrost zmiennej zależnej;
oznacza silną „zgodność” uporządkowania rang (zależność monotoniczną rosnącą), tj. wzrostowi zmiennej niezależnej odpowiada wzrost zmiennej zależnej;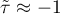 oznacza silną „niezgodność” uporządkowania rang (zależność monotoniczną malejącą), tj. wzrostowi zmiennej niezależnej odpowiada spadek zmiennej zależnej;
oznacza silną „niezgodność” uporządkowania rang (zależność monotoniczną malejącą), tj. wzrostowi zmiennej niezależnej odpowiada spadek zmiennej zależnej;- gdy współczynnik korelacji
 przyjmuje wartość równą lub bardzo bliską zeru wówczas nie istnieje monotoniczna zależność między badanymi parametrami (ale może istnieć związek niemonotoniczny np. sinusoidalny).
przyjmuje wartość równą lub bardzo bliską zeru wówczas nie istnieje monotoniczna zależność między badanymi parametrami (ale może istnieć związek niemonotoniczny np. sinusoidalny).
Współczynnik 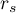 Spearmana a współczynnik
Spearmana a współczynnik  Kendalla
Kendalla
- dla skali interwałowej z normalnością rozkładu obu cech wartość
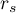 daje rezultaty bliższe wartości
daje rezultaty bliższe wartości 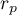 natomiast wartości
natomiast wartości  może znacznie różnić się od
może znacznie różnić się od 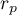 ,
, - wartość
 jest mniejsza bądź równa wartości
jest mniejsza bądź równa wartości 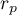 ,
,  jest nieobciążonym estymatorem parametru populacji
jest nieobciążonym estymatorem parametru populacji 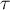 , podczas gdy wartość
, podczas gdy wartość 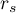 nie jest estymatorem nieobciążonym parametru
nie jest estymatorem nieobciążonym parametru 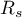 .
.
Przykład c.d. (plik wiek-wzrost.pqs)
1)
Kendall M.G. (1938), A new measure of rank correlation. Biometrika, 30, 81-93
statpqpl/korelpl/nparpl/wsppl.txt · ostatnio zmienione: 2022/01/28 17:10 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

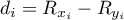 - różnica
- różnica  liczność
liczność 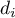 .
.
