Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:korelpl:parpl:rpbetapl
Istotność współczynnika nachylenia prostej
Test t do sprawdzania istotności współczynników równania regresji liniowej
Test ten służy do weryfikacji hipotezy o braku zależności liniowej pomiędzy badanymi cechami populacji i opiera się na współczynniku nachylenia prostej wyliczonym dla próby. Im wartość współczynnika 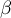 będzie bliższa 0, tym słabszą zależność dopasowana prosta przedstawia.
będzie bliższa 0, tym słabszą zależność dopasowana prosta przedstawia.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu badanych cech w populacji lub normalność reszt modelu.
Hipotezy:
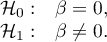
Statystyka testowa ma postać:
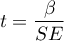
gdzie:
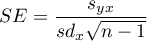 ,
,
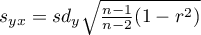 ,
,
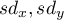 - odchylenie standardowe wartości cechy
- odchylenie standardowe wartości cechy  i cechy
i cechy  .
.
Wartość statystyki testowej nie może być wyznaczona, gdy 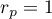 lub
lub 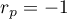 albo, gdy
albo, gdy 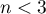 .
.
Statystyka testowa ma rozkład t-Studenta z 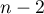 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Predykcja
polega na przewidywaniu wartości jednej ze zmiennych (najczęściej zmiennej zależnej 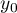 ) na podstawie wartości innej zmiennej (najczęściej zmiennej niezależnej
) na podstawie wartości innej zmiennej (najczęściej zmiennej niezależnej 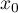 ). Dokładność wyznaczonej wartości określają obliczone dla niej przedziały predykcji.
). Dokładność wyznaczonej wartości określają obliczone dla niej przedziały predykcji.
- Interpolacja polega na przewidywaniu wartości zadanej zmiennej leżącej wewnątrz obszaru, dla którego wykonaliśmy model regresji. Interpolacja jest więc z reguły procedurą bezpieczną - zakłada się tu jedynie ciągłość funkcji wyrażającej zależność obu zmiennych.
- Ekstrapolacja polega na przewidywaniu wartości zadanej zmiennej leżącej poza obszarem, dla którego zbudowaliśmy model regresji. W przeciwieństwie do interpolacji, ekstrapolacja bywa często zabiegiem ryzykownym i dokonuje się jej jedynie w niewielkiej odległości od obszaru, dla którego powstał model regresji. Podobnie jak w interpolacji zakłada się ciągłość funkcji wyrażającej zależność obu zmiennych.
Analiza reszt modelu - wyjaśnienie w module Regresja Wieloraka.
Okno z ustawieniami opcji zależności liniowej Pearsona wywołujemy poprzez menu Statystyka→Testy parametryczne→zależność liniowa (r-Pearsona) lub poprzez ''Kreator''.
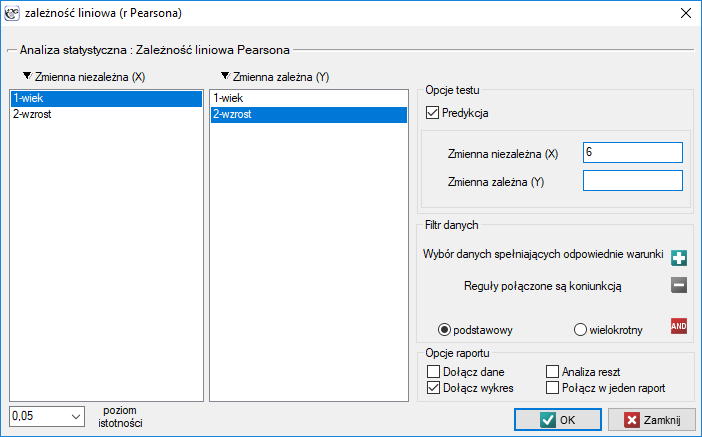
Przykład (plik wiek-wzrost.pqs)
Wśród uczniów pewnej szkoły baletowej badano zależność pomiędzy wiekiem a wzrostem. W tym celu pobrano próbę obejmującą szesnaścioro dzieci i zapisano dla nich następujące wyniki pomiaru tych cech:
(wiek, wzrost): (5, 128) (5, 129) (5, 135) (6, 132) (6, 137) (6, 140) (7, 148) (7, 150) (8, 135) (8, 142) (8, 151) (9, 138) (9, 153) (10, 159) (10, 160) (10, 162).}
Hipotezy:

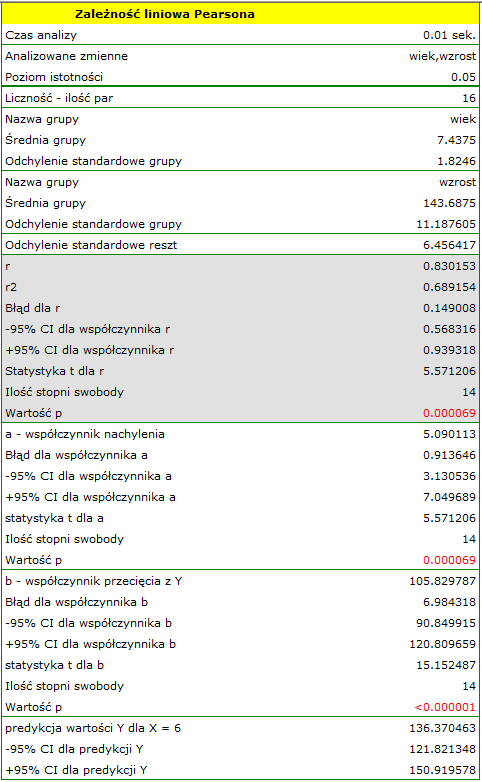
Porównując wartość  =0.000069 z poziomem istotności
=0.000069 z poziomem istotności  stwierdzamy, że istnieje zależność liniowa pomiędzy wiekiem a wzrostem dla populacji dzieci badanej szkoły. Zależność ta jest wprost proporcjonalna, tzn. wraz ze wzrostem wieku dzieci rośnie wysokość ciała.
stwierdzamy, że istnieje zależność liniowa pomiędzy wiekiem a wzrostem dla populacji dzieci badanej szkoły. Zależność ta jest wprost proporcjonalna, tzn. wraz ze wzrostem wieku dzieci rośnie wysokość ciała.
Współczynnik korelacji liniowej Pearsona, a zatem siła związku liniowego pomiędzy wiekiem a wzrostem wynosi 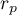 =0.8302. Współczynnik determinacji
=0.8302. Współczynnik determinacji 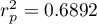 oznacza, że ok. 69% zmienności wzrostu jest tłumaczona zmiennością wieku.
oznacza, że ok. 69% zmienności wzrostu jest tłumaczona zmiennością wieku.
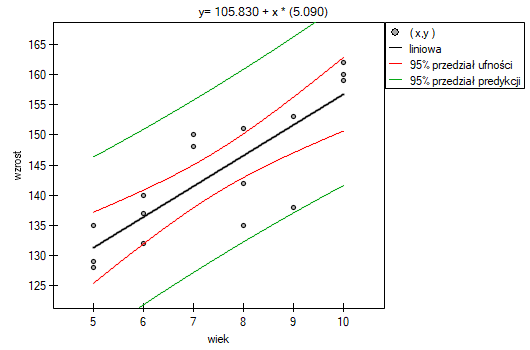
Z równania regresji postaci:
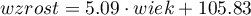 można wyliczyć predykcyjną wartość dla dziecka w wieku np. 6 lat. Przewidywany wzrost takiego dziecka wynosi 136.37cm.
można wyliczyć predykcyjną wartość dla dziecka w wieku np. 6 lat. Przewidywany wzrost takiego dziecka wynosi 136.37cm.
statpqpl/korelpl/parpl/rpbetapl.txt · ostatnio zmienione: 2022/02/01 10:30 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

