Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Wykresy » Lokalne techniki wygładzania liniowego
Pasek boczny
statpqpl:plotpl:lowess
Lokalne techniki wygładzania liniowego
LOWESS
LOWESS (ang.locally weighted scatterplot smoothing) znana również pod nazwą LOESS (ang. locally estimated scatterplot smoothing) jest jedną z wielu „nowoczesnych” metod modelowania opartych na metodzie najmniejszych kwadratów. LOESS łączy w sobie prostotę regresji liniowej z elastycznością regresji nieliniowej. Oszacowanie regresji lokalnej (locally weighted regression) zostało niezależnie wprowadzone na kilku różnych polach pod koniec XIX i na początku XX wieku (Henderson, 1916 1); Schiaparelli, 18662)). W literaturze statystycznej metodę tę wprowadzono niezależnie z różnych punktów widzenia pod koniec lat siedemdziesiątych min. Cleveland, 1979 3). Metoda wykorzystana w programie PQstat opiera się na tej właśnie pracy. Podstawową zasadą jest to, że funkcja gładka może być dobrze przybliżona przez wielomian niskiego stopnia (w programie zastosowano funkcję liniową czyli wielomian pierwszego stopnia) w sąsiedztwie dowolnego punktu x.
Algorytm postępowania:
(1)
Dla każdego punktu zbioru danych budujemy okno zawierające sąsiednie elementy. To jak dużo elementów znajdzie się w oknie wyznacza parametr wygładzania 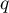 . Czym wyższa jego wartość, tym bardziej wygładzoną uzyskamy funkcję. Jeśli parametr ten wyniesie np. 0.2, wówczas w oknie znajdzie się około 20% danych i one posłużą do budowania wielomianu (tutaj jednomianu tzn. funkcji liniowej).
. Czym wyższa jego wartość, tym bardziej wygładzoną uzyskamy funkcję. Jeśli parametr ten wyniesie np. 0.2, wówczas w oknie znajdzie się około 20% danych i one posłużą do budowania wielomianu (tutaj jednomianu tzn. funkcji liniowej).
Ze względu na konieczność utrzymania symetrii okna tzn. dane w oknie powinny znajdować się powyżej i poniżej punktu, dla którego budujemy model, liczba elementów w oknie powinna być nieparzysta. Dlatego też uzyskana na podstawie parametru 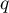 liczba elementów zaokrąglana jest w górę do pierwszej liczby nieparzystej. W ten sposób powstaje okno zawierające element
liczba elementów zaokrąglana jest w górę do pierwszej liczby nieparzystej. W ten sposób powstaje okno zawierające element 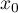 oraz odpowiednią liczbę
oraz odpowiednią liczbę 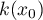 elementów znajdujących się przed tym elementem i za tym elementem w uporządkowanym zbierze danych.
elementów znajdujących się przed tym elementem i za tym elementem w uporządkowanym zbierze danych.
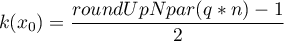
Przykładowo, gdy w oknie ma się znaleźć 7 elementów, to znajdzie się w nim element 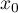 oraz trzy wcześniejsze i trzy późniejsze elementy próby. Okno wyznaczone dla pierwszych i ostatnich elementów próby jest tej samej wielkości, ale badany element nie jest w nim umieszczony symetrycznie tzn. na środku.
oraz trzy wcześniejsze i trzy późniejsze elementy próby. Okno wyznaczone dla pierwszych i ostatnich elementów próby jest tej samej wielkości, ale badany element nie jest w nim umieszczony symetrycznie tzn. na środku.
(2)
W każdym punkcie zbioru danych dopasowany jest wielomian niskiego stopnia (tutaj funkcja liniowa) do podzbioru zlokalizowanych w oknie danych. Dopasowanie dokonywane jest przy użyciu ważonej metody najmniejszych kwadratów, co daje większą wagę punktom w pobliżu punktu, którego odpowiedź jest szacowana, i mniejszą wagę punktom oddalonym. W ten sposób do każdego punktu przypisana jest inna formuła funkcji wielomianu (tutaj funkcji liniowej).
Stosowane w ważonej metodzie najmniejszych kwadratów wagi mogą być ustawiane dość elastycznie, ale punkty odległe od zadanego muszą mieć mniejszą wagę niż punkty w pobliżu. Tutaj posłużono się wagami zaproponowanymi przez Clevelanda tzw. tricube
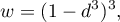 gdzie odległość
gdzie odległość 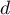 od punku
od punku 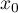 wyniosła 0 -dla punktów znajdujących się poza wyznaczonym oknem i była podana jako rzeczywista odległość między punktami, ale znormalizowana do przedziału [0,1] -dla punktów zlokalizowanych w oknie, tak by maksymalne odległości we wszystkich oknach były takie same.
wyniosła 0 -dla punktów znajdujących się poza wyznaczonym oknem i była podana jako rzeczywista odległość między punktami, ale znormalizowana do przedziału [0,1] -dla punktów zlokalizowanych w oknie, tak by maksymalne odległości we wszystkich oknach były takie same.
(3)
W każdym punkcie, na podstawie przypisanej do niego formuły wielomianu (tutaj funkcji liniowej) obliczana jest wartość funkcji 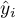 . Na podstawie punktów
. Na podstawie punktów  oraz estymowanych tą metodą punktów
oraz estymowanych tą metodą punktów 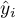 wyrysowywana jest wygładzona i dopasowana do danych funkcja.
wyrysowywana jest wygładzona i dopasowana do danych funkcja.
Wygładzanie jądrowe
Oszacowanie funkcji regresji metodą wygładzania jądrowego jest czasem nazywane oszacowaniem Nadaraya-Watson (Nadaraya, 19644); Watson, 19645)). Szacowanie jądra jest średnią ważoną obserwacji w oknie wygładzania:
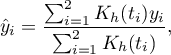
gdzie 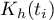 jest funkcją jądra opisaną w rozdziale Estymacja jądrowa.
jest funkcją jądra opisaną w rozdziale Estymacja jądrowa.
Parametr wygładzania 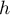 (ang. bandwidth) ma decydujący wpływ na uzyskany estymator. Im wyższa wartość parametru wygładzania, tym stopień wygładzenia jest większy. Do wyboru mamy możliwość dowolnego wyboru parametru wygładzania poprzez ustawienie wartości użytkownika. Możliwy jest również automatyczny dobór tej wielkości poprzez metodę SNR, SROT lub OS. Znacznie mniejszy wpływ na uzyskany wynik ma funkcja jądra. Do wyboru mamy jądro: Gaussa, w postaci funkcji jednostajnej (prostokąt), trójkątnej, Epanechnikova, quartic lub biweight (czwartego stopnia). Opis poszczególnych wielkości parametru wygładzania i funkcji jądra można znaleźć we wspomnianym rozdziale.
(ang. bandwidth) ma decydujący wpływ na uzyskany estymator. Im wyższa wartość parametru wygładzania, tym stopień wygładzenia jest większy. Do wyboru mamy możliwość dowolnego wyboru parametru wygładzania poprzez ustawienie wartości użytkownika. Możliwy jest również automatyczny dobór tej wielkości poprzez metodę SNR, SROT lub OS. Znacznie mniejszy wpływ na uzyskany wynik ma funkcja jądra. Do wyboru mamy jądro: Gaussa, w postaci funkcji jednostajnej (prostokąt), trójkątnej, Epanechnikova, quartic lub biweight (czwartego stopnia). Opis poszczególnych wielkości parametru wygładzania i funkcji jądra można znaleźć we wspomnianym rozdziale.
Okno z ustawieniami opcji wykresu punktowego z dopasowaną funkcją metodą LOWESS lub poprzez wygładzanie jądrowe znajdziemy w różnych analizach. Wykres ten możemy również wykonać poprzez menu Wykresy→Wykres punktowy.
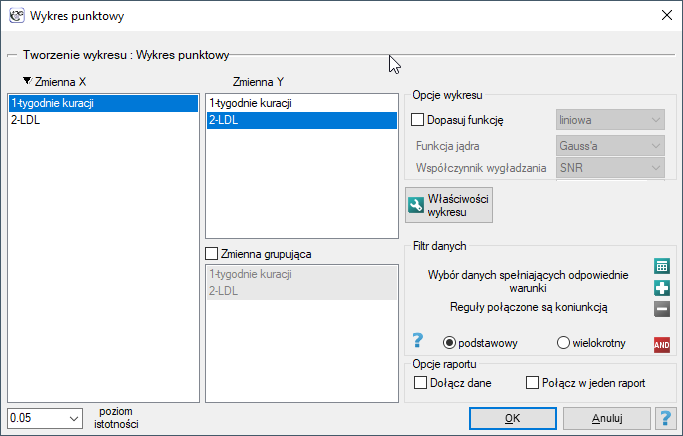
Przykład c.d. (plik LDL tygodnie.pqs)
Badano skuteczność nowej terapii, której celem jest obniżenie poziomu cholesterolu we frakcji LDL. Przebadano 88 osób na różnym etapie kuracji. Sprawdzimy, czy wraz z upływem czasu stosowania kuracji (czas w tygodniach) poziom cholesterolu LDL spada i się stabilizuje.
Wyniki przedstawiono początkowo dopasowując linię prostą wskazującą kierunek badanej zależności.
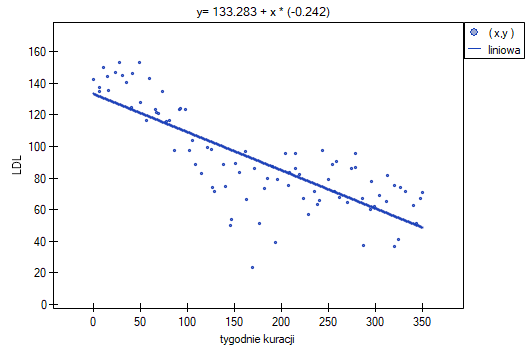
Jednak ten sposób przedstawienia danych nie oddaje w pełni zachodzących zależności. Z ułożenia punktów można zauważyć, że zależność ta jest początkowo malejąca, a po 150 tygodniach zaczyna się stabilizować. Zależność przedstawiono ponownie korzystając z metody LOWESS oraz z wygładzania jądrowego Gaussa.
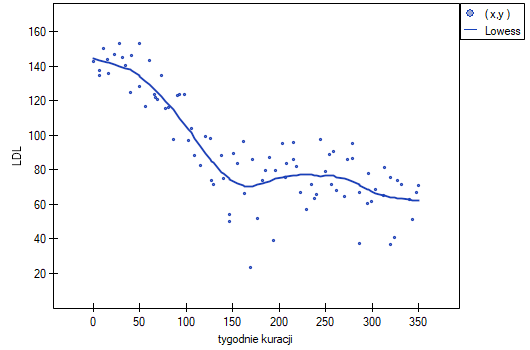
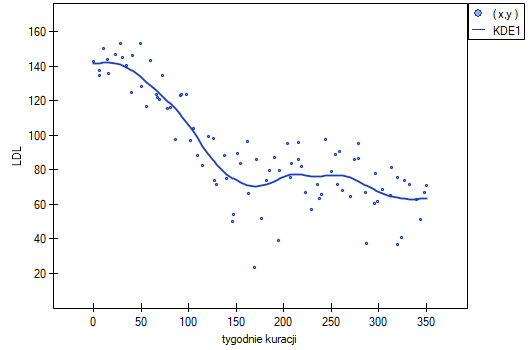
Obydwa sposoby tzn. zarówno LOWESS jak i wygładzanie jądrowe dały zbliżone wyniki i znacznie lepiej opisały dane, wskazując na początkowy spadek LDL a następnie jego stabilizację na poziomie bliskim 70 mg/dl.
1)
Henderson, R. (1916). Note on graduation by adjusted average.Transactionsof the Actuarial Society of America, 17:43–48
2)
Schiaparelli, G. V.(1866). Sul modo di ricavare la vera espressione delle leggidelta natura dalle curve empiricae.Effemeridi Astronomiche di Milano perl’Arno, 857:3–56
3)
Cleveland, W. S. (1979). Robust Locally Weighted Regression and Smoothing Scatterplots. Journal of the American Statistical Association. 74 (368): 829–836.
4)
Nadaraya, E. A. (1964). On Estimating Regression. Theory of Probability and Its Applications. 9 (1): 141–2
5)
Watson, G. S. (1964). Smooth regression analysis. Sankhyā: The Indian Journal of Statistics, Series A. 26 (4): 359–372.
statpqpl/plotpl/lowess.txt · ostatnio zmienione: 2021/01/13 22:02 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

