Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:plotpl:kde1pl
Spis treści
Estymacja jądrowa
Jednowymiarowy estymator jądrowy
Jednowymiarowy jądrowy estymator gęstości pozwala na przybliżenie gęstości rozkładu danych tworząc wygładzoną krzywą gęstości w sposób nieparametryczny. Dzięki niemu uzyskuje się lepszą estymację gęstości niż daje tradycyjny histogram, którego kolumny tworzą funkcję schodkową.
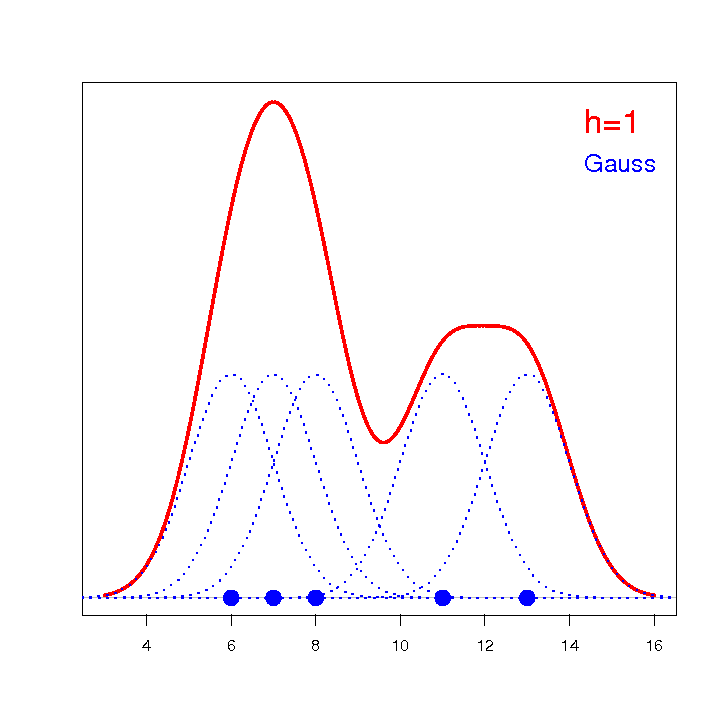
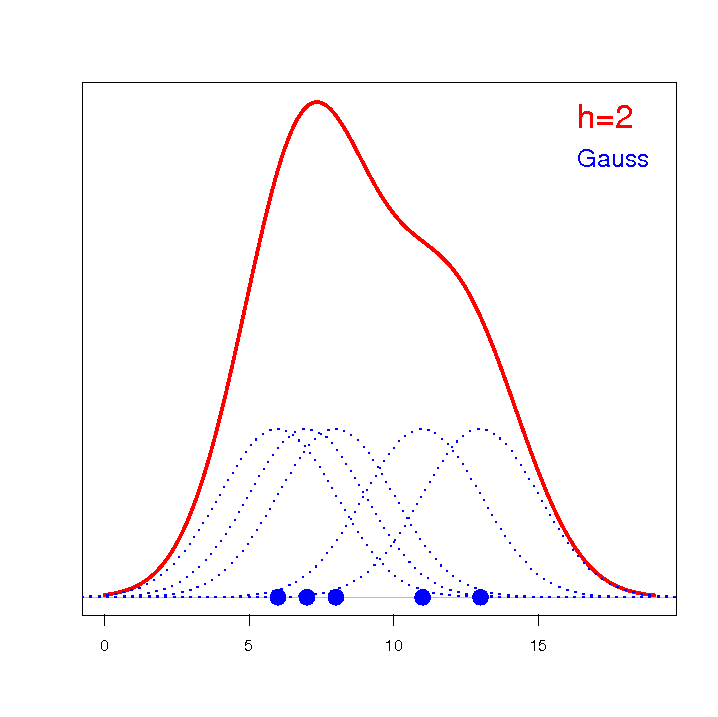
Estymator jądrowy definiowany jest w oparciu o odpowiednio wygładzone jądro 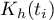 . Parametr wygładzania
. Parametr wygładzania 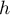 (ang. bandwidth) ma decydujący wpływ na uzyskany estymator. Im wyższa wartość parametru wygładzania, tym stopień wygładzenia jest większy.
(ang. bandwidth) ma decydujący wpływ na uzyskany estymator. Im wyższa wartość parametru wygładzania, tym stopień wygładzenia jest większy.
Dla każdego punktu 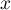 z zakresu określonego przez dane wyznacza się gęstość czyli podaje wartość estymatora jądrowego w tym punkcie. Estymator ten powstaje poprzez zsumowanie wartości funkcji jąder
z zakresu określonego przez dane wyznacza się gęstość czyli podaje wartość estymatora jądrowego w tym punkcie. Estymator ten powstaje poprzez zsumowanie wartości funkcji jąder 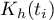 w tym punkcie:
w tym punkcie:
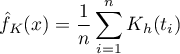
Jeśli poszczególnym przypadkom nadamy wagi 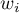 , wówczas możemy zbudować ważony jądrowy estymator gęstości definiowany wzorem:
, wówczas możemy zbudować ważony jądrowy estymator gęstości definiowany wzorem:
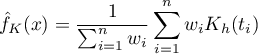
Współczynniki wygładzania
- Użytkownika - daje możliwość wybrania dowolnego współczynnika wygładzania wskazanego przez użytkownika, przy czym współczynnik ten musi być dodatni.
- Użytkownika skalowane - jest ustalane tak, by można było zmieniać funkcję jądra pozostając przy wygładzeniu jakie wybrane zostało wcześniej dla jądra Gaussa. W praktyce wybierając inną funkcję niż Gaussa współczynnik wygładzania zostaje przeskalowany (Scott, D. W. 19921)), przez co wygładzenie pozostaje na podobnym poziomie jaki był dla funkcji Gaussa. Daje to wygodę przełączania się pomiędzy różnymi jądrami bez rozważania skalowania parametru wygładzania. Przeliczenia dotyczące skalowania dokonywane są w oparciu o odchylenie standardowe:
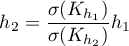
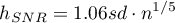
Dla jądra innego niż Gaussa, współczynnik wygładzania podlega skalowaniu (Scott D. W., 19924))
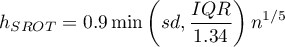
Dla jądra innego niż Gaussa, współczynnik wygładzania podlega skalowaniu (Scott D. W., 19927))
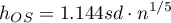
Dla jądra innego niż Gaussa, współczynnik wygładzania podlega skalowaniu (Scott D. W., 199210))
Funkcja jądra w mniejszym zakresie niż parametr wygładzania wpływa na uzyskaną wartość estymatora jądrowego. Jądro jest funkcją gęstości prawdopodobieństwa budowaną wokół każdego punktu danych  . Zwykle jest to funkcja symetryczna osiągająca maksimum w punkcie
. Zwykle jest to funkcja symetryczna osiągająca maksimum w punkcie  , a zmniejszająca swoje wartości wraz z oddalaniem się (wzrostem odległości
, a zmniejszająca swoje wartości wraz z oddalaniem się (wzrostem odległości 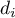 ) od tego punktu. Odległość od analizowanego punktu jest modyfikowana przez parametr wygładzania
) od tego punktu. Odległość od analizowanego punktu jest modyfikowana przez parametr wygładzania 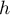 zgodnie z wzorem:
zgodnie z wzorem: 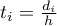 .
.
W zależności od potrzeb funkcja jądra może przyjmować postać funkcji:
- Gaussa
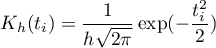
- jednostajnej (prostokąt)
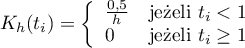
- trójkątnej
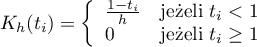
- Epanechnikova
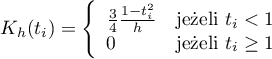
- quartic lub biweight (czwartego stopnia)
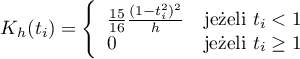
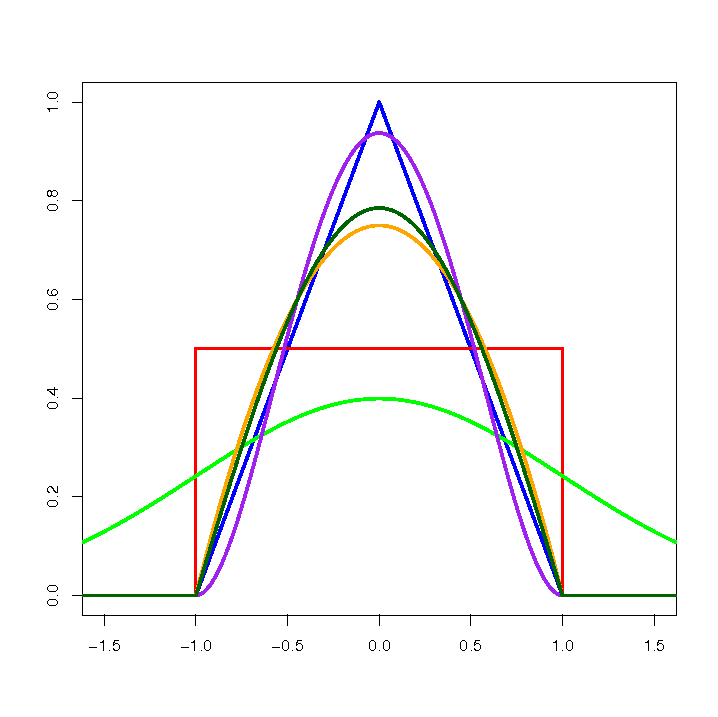
![LaTeX
\textcolor{green}{Gaussa}
\textcolor{red}{jednostajna}
\textcolor{blue}{trójkątna}
\textcolor{orange}{Epanechnikova}
\textcolor[rgb]{0,0.58,0}{quartic/biweight}](/lib/exe/fetch.php?media=wiki:latex:/imgef368a2a394bf425fa6fccb67382004e.png)
Przykład (plik BMI.pqs)
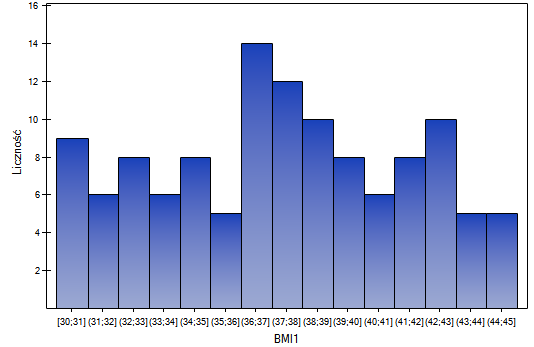
Wyliczono wartości współczynnika wagowo-wzrostowego BMI1 dla pewnej grupy osób otyłych. Przedstawiono ich rozkład za pomocą histogramu z podziałem wartości co 1 jednostkę BMI. Dane zobrazowano również za pomocą jądrowego estymatora gęstości wybierając Gaussowską funkcję jądra i ustawiając współczynniki wygładzania odpowiednio: 0.5, 1, 2.
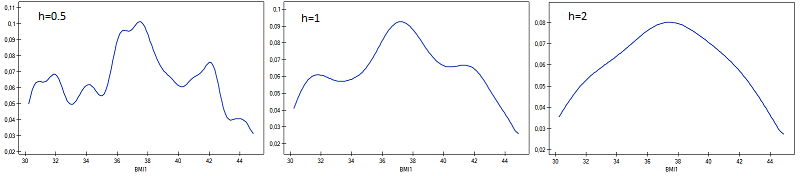
Współczynniki wygładzania estymatora jądrowego sugerowane przez metody SROT, SNR i OS osiągają wielkości pomiędzy 1.4 a 2.
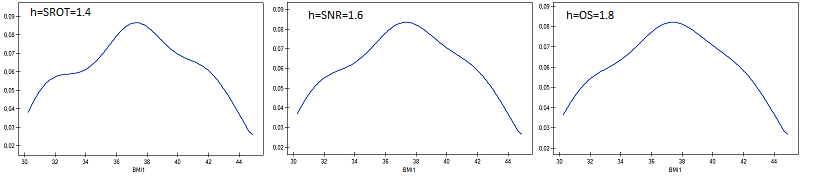
1)
, 4)
, 7)
, 10)
Scott D. W., (1992), Multivariate Density Estimation. Theory, Practice and Visualization. New York: Wiley
2)
, 5)
Silverman B. W., (1986), Density estimation for statistics and data analysis, London: Chapman and Hall
3)
, 6)
Jones M. C., Marron J. S., Sheather S. J., (1996)., A brief survey of bandwidth selection for density estimation. J. Amer. Statist. Assoc. 91 401–407
8)
Terrell G.R., Scott D. W. (1985), Oversmoothed nonparametric density estimates. Journal of the American Statistical Association 80, 209-214
9)
Terrell G. R. (1990), The maximal smoothing principle in density estimation. Journal of the American Statistical Association 85, 470–477
statpqpl/plotpl/kde1pl.txt · ostatnio zmienione: 2022/02/11 11:48 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

