Spis treści
Comparison - one group
{\ovalnode{A}{\hyperlink{rozklad_normalny}{\begin{tabular}{c}Are\\the data\\normally\\distributed?\end{tabular}}}}
\rput[br](2.9,7.2){\rnode{B}{\psframebox{\hyperlink{test_t_student}{\begin{tabular}{c}Single-sample\\t-test\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{A}{B}
\rput(2.2,10.4){Y}
\rput(4.3,12.5){N}
\rput(7.5,14){\hyperlink{porzadkowa}{Ordinal scale}}
\rput[br](8.9,11.5){\rnode{C}{\psframebox{\hyperlink{test_wilcoxon_rangowanych_znakow}{\begin{tabular}{c}Wilcoxon\\(signed-ranks)\\test\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{A}{C}
\rput(12.5,14){\hyperlink{nominalna}{Nominal scale}}
\rput[br](13.8,11.09){\rnode{D}{\psframebox{\begin{tabular}{c}\hyperlink{test_chi_kwadrat_dobroci}{$\chi^2$ test}\\\hyperlink{test_chi_kwadrat_dobroci}{(goodness-of-fit),}\\\hyperlink{test_z_dla_proporcji}{tests for} \\\hyperlink{test_z_dla_proporcji}{one proportion}\\\end{tabular}}}}
\rput(4.0,10){\hyperlink{testy_normalnosci}{normality tests}}
\psline[linestyle=dotted]{<-}(3.4,11.2)(4,10.2)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img8031848e672ebdef425d4303c6cbd3e7.png)
Parametric tests
The t-test for a single sample
The single-sample 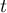 test is used to verify the hypothesis, that an analysed sample with the mean (
test is used to verify the hypothesis, that an analysed sample with the mean (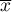 ) comes from a population, where mean (
) comes from a population, where mean (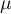 ) is a given value.
) is a given value.
Basic assumptions:
- measurement on an interval scale,
- normality of distribution of an analysed feature.
Hypotheses:
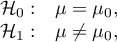
where:
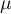 – mean of an analysed feature of the population represented by the sample,
– mean of an analysed feature of the population represented by the sample,
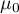 – a given value.
– a given value.
The test statistic is defined by:
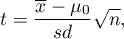
where:
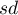 – standard deviation from the sample,
– standard deviation from the sample,
 – sample size.
– sample size.
The test statistic has the t-Student distribution with  degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Note
Note, that: If the sample is large and you know a standard deviation of the population, then you can calculate a test statistic using the formula:
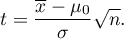 The statistic calculated this way has the normal distribution. If
The statistic calculated this way has the normal distribution. If 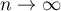
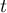 -Student distribution converges to the normal distribution
-Student distribution converges to the normal distribution 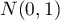 . In practice, it is assumed, that with
. In practice, it is assumed, that with  the
the 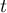 -Student distribution may be approximated with the normal distribution.
-Student distribution may be approximated with the normal distribution.
Standardized effect size.
The Cohen's d determines how much of the variation occurring is the difference between the averages.
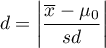 .
.
When interpreting an effect, researchers often use general guidelines proposed by Cohen 1) defining small (0.2), medium (0.5) and large (0.8) effect sizes.
The settings window with the Single-sample <latex>$t$</latex>-test can be opened in Statistics menu→Parametric tests→t-test or in ''Wizard''.
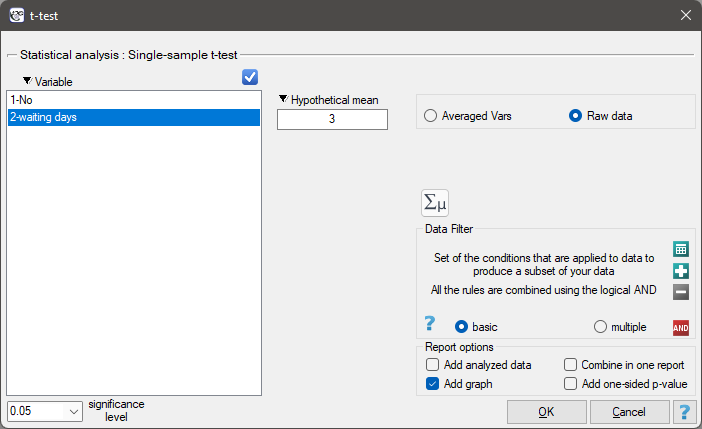
Note
Calculations can be based on raw data or data that are averaged like: arithmetic mean, standard deviation and sample size.
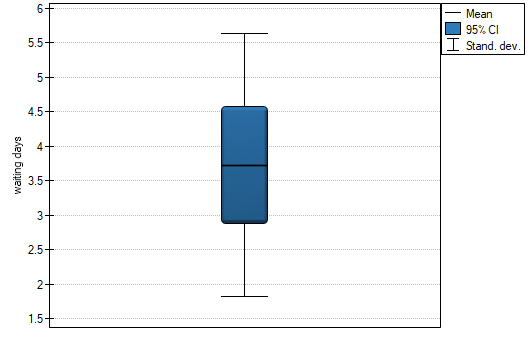
You want to check if the time of awaiting for a delivery by some courier company is 3 days on the average 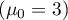 . In order to calculate it, there are 22 persons chosen by chance from all clients of the company as a sample. After that, there are written information about the number of days passed since the delivery was sent till it is delivered. There are following values: (1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7).
. In order to calculate it, there are 22 persons chosen by chance from all clients of the company as a sample. After that, there are written information about the number of days passed since the delivery was sent till it is delivered. There are following values: (1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7).
The number of awaiting days for the delivery in the analysed population fulfills the assumption of normality of distribution.
Hypotheses:

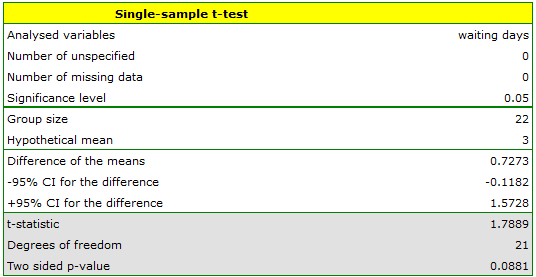

Comparing the  value = 0.0881 of the
value = 0.0881 of the 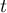 -test with the significance level
-test with the significance level  we draw the conclusion, that there is no reason to reject the null hypothesis which informs that the average time of awaiting for the delivery, which is supposed to be delivered by the analysed courier company is 3. For the tested sample, the mean is
we draw the conclusion, that there is no reason to reject the null hypothesis which informs that the average time of awaiting for the delivery, which is supposed to be delivered by the analysed courier company is 3. For the tested sample, the mean is 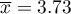 and the standard deviation is
and the standard deviation is 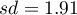 .
.
The Single-Sample Chi-square Test for a Population Variance
Basic assumptions:
- measurement on an interval scale,
- normality of distribution of an analysed feature.
Hypotheses:
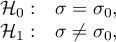
where:
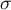 – standard deviation of a characteristic in the population represented by the sample,
– standard deviation of a characteristic in the population represented by the sample,
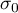 – setpoint.
– setpoint.
The test statistic is defined by:
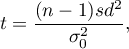
where:
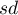 – standard deviation in the sample,
– standard deviation in the sample,
 – sample size.
– sample size.
The test statistic has the Chi-square distribution with the degrees of freedom determined by the formula: 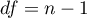 .
.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Whereby, if the standard deviation value is less than the setpoint, the  value is calculated as the doubled value of the area under the chi-square distribution curve to the left of the corresponding critical value, and if it is greater than the setpoint, it is the doubled value of the corresponding area to the right.
value is calculated as the doubled value of the area under the chi-square distribution curve to the left of the corresponding critical value, and if it is greater than the setpoint, it is the doubled value of the corresponding area to the right.
he settings window with the Chi-test for variance w can be opened in Statistics menu→Parametric tests→Chi-square test for variance.
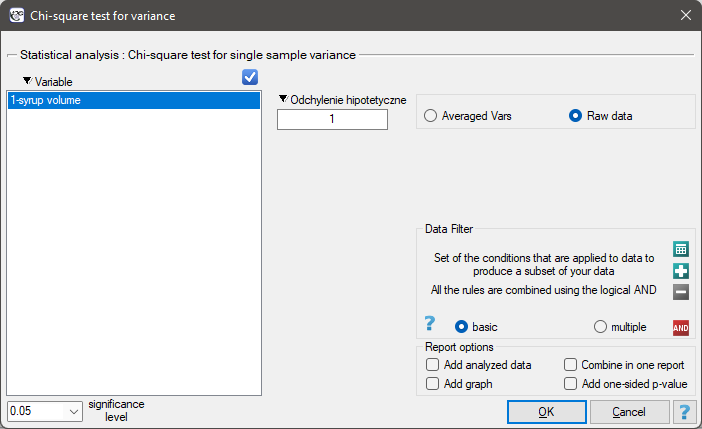
Note
Calculations can be based on raw data or data that are averaged like: standard deviation and sample size.
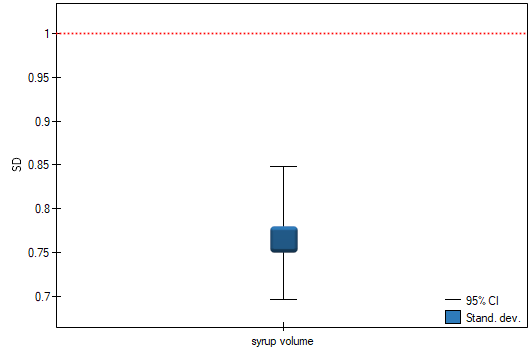
Before starting the production of another batch of a certain cough syrup, control measurements of the volume of syrup poured into the bottles were made. The technical documentation of the dosing device shows that the permissible variation in syrup volume measured by the standard deviation is 1ml. It should be verified that the tested device is working properly.
The distribution of the volume of syrup poured into the bottles was checked (with the Lilliefors test) obtaining a result consistent with this distribution. The analysis concerning the standard deviation can therefore be performed with the chi-square test for variance
Hypotheses:


Comparing the 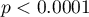 value of the
value of the  test with the significance level
test with the significance level  we find that the scatter of the dispensing device is different from 1ml. However, we can consider the performance of the device as correct because the standard deviation of the sample is 0.76, which is significantly less than the acceptable value from the technical documentation.
we find that the scatter of the dispensing device is different from 1ml. However, we can consider the performance of the device as correct because the standard deviation of the sample is 0.76, which is significantly less than the acceptable value from the technical documentation.
Non-parametric tests
The Wilcoxon test (signed-ranks)
The Wilcoxon signed-ranks test is also known as the Wilcoxon single sample test, Wilcoxon (1945, 1949)2). This test is used to verify the hypothesis, that the analysed sample comes from the population, where median (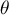 ) is a given value.
) is a given value.
Basic assumptions:
- measurement on an ordinal scale or on an interval scale.
Hypotheses:
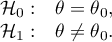
where:
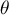 – median of an analysed feature of the population represented by the sample,
– median of an analysed feature of the population represented by the sample,
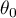 – a given value.
– a given value.
Now you should calculate the value of the test statistics  (
(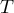 – for the small sample size), and based on this
– for the small sample size), and based on this  value.
value.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Note
Depending on the size of the sample, the test statistic takes a different form:
- for a small sample size
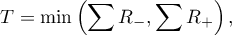
where:
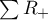 and
and 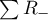 are adequately: a sum of positive and negative ranks.
are adequately: a sum of positive and negative ranks.
This statistic has the Wilcoxon distribution.
- for a large sample size
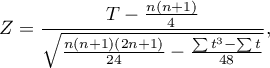
where:
 - the number of ranked signs (the number of ranks),
- the number of ranked signs (the number of ranks),
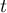 - the number of cases being included in the interlinked rank.
- the number of cases being included in the interlinked rank.
The test statistic formula  includes the correction for ties. This correction should be used when ties occur (when there are no ties, the correction is not calculated, because
includes the correction for ties. This correction should be used when ties occur (when there are no ties, the correction is not calculated, because 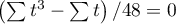 .
.
 statistic asymptotically (for a large sample size) has the normal distribution.
Continuity correction of the Wilcoxon test (Marascuilo and McSweeney (1977)3))
statistic asymptotically (for a large sample size) has the normal distribution.
Continuity correction of the Wilcoxon test (Marascuilo and McSweeney (1977)3))
A continuity correction is used to enable the test statistic to take in all values of real numbers, according to the assumption of the normal distribution. Test statistic with a continuity correction is defined by:
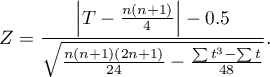
Standardized effect size
The distribution of the Wilcoxon test statistic is approximated by the normal distribution, which can be converted to an effect size 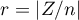 4) to then obtain the Cohen's d value according to the standard conversion used for meta-analyses:
4) to then obtain the Cohen's d value according to the standard conversion used for meta-analyses:
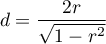
When interpreting an effect, researchers often use general guidelines proposed by 5) defining small (0.2), medium (0.5) and large (0.8) effect sizes.
The settings window with the Wilcoxon test (signed-ranks) can be opened in Statistics menu
NonParametric tests→Wilcoxon (signed-ranks) or in ''Wizard''.
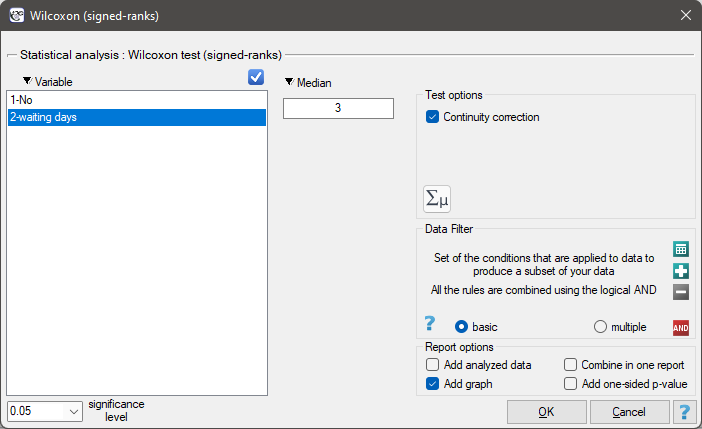
EXAMPLE cont. (courier.pqs file)
Hypotheses:

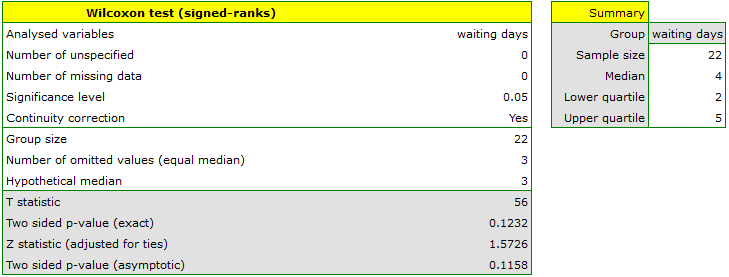
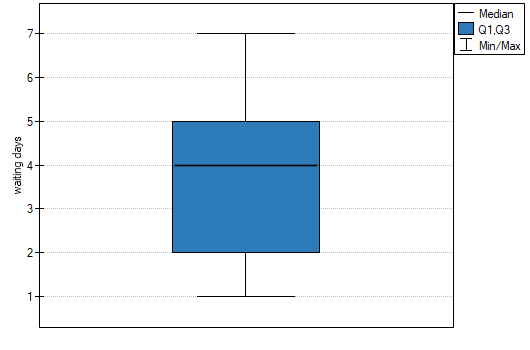
Comparing the p-value = 0.1232 of Wilcoxon test based on 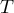 statistic with the significance level
statistic with the significance level  we draw the conclusion, that there is no reason to reject the null hypothesis informing us, that usually the number of awaiting days for the delivery which is supposed to be delivered by the analysed courier company is 3. Exactly the same decision you would make basing on the p-value = 0.1112 or p-value = 0.1158 of Wilcoxon test based upon
we draw the conclusion, that there is no reason to reject the null hypothesis informing us, that usually the number of awaiting days for the delivery which is supposed to be delivered by the analysed courier company is 3. Exactly the same decision you would make basing on the p-value = 0.1112 or p-value = 0.1158 of Wilcoxon test based upon  statistic or
statistic or  with correction for continuity.
with correction for continuity.
The Chi-square goodness-of-fit test
The  test (goodnes-of-fit) is also called the one sample
test (goodnes-of-fit) is also called the one sample  test and is used to test the compatibility of values observed for
test and is used to test the compatibility of values observed for 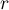 (
(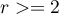 ) categories
) categories 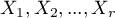 of one feature
of one feature  with hypothetical expected values for this feature. The values of all
with hypothetical expected values for this feature. The values of all  measurements should be gathered in a form of a table consisted of
measurements should be gathered in a form of a table consisted of 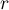 rows (categories:
rows (categories: 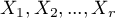 ). For each category
). For each category 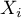 there is written the frequency of its occurence
there is written the frequency of its occurence 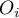 , and its expected frequency
, and its expected frequency 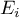 or the probability of its occurence
or the probability of its occurence 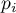 . The expected frequency is designated as a product of
. The expected frequency is designated as a product of 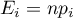 . The built table can take one of the following forms:
. The built table can take one of the following forms:
![LaTeX \begin{tabular}[t]{c@{\hspace{1cm}}c}
\begin{tabular}{c|c c}
$X_i$ categories& $O_i$ & $E_i$ \\\hline
$X_1$ & $O_1$ & $E_i$ \\
$X_2$ & $O_2$ & $E_2$ \\
... & ... & ...\\
$X_r$ & $O_r$ & $E_r$ \\
\end{tabular}
&
\begin{tabular}{c|c c}
$X_i$ categories& $O_i$ & $p_i$ \\\hline
$X_1$ & $O_1$ & $p_1$ \\
$X_2$ & $O_2$ & $p_2$ \\
... & ... & ...\\
$X_r$ & $O_r$ & $p_r$ \\
\end{tabular}
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img77385665f77e4a4583e9d51979a49d71.png)
Basic assumptions:
- measurement on a nominal scale - any order is not taken into account,
- large expected frequencies (according to the Cochran interpretation (1952)6),
- observed frequencies total should be exactly the same as an expected frequencies total, and the total of all
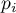 probabilities should come to 1.
probabilities should come to 1.
Hypotheses:
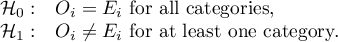
Test statistic is defined by:
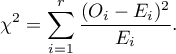
This statistic asymptotically (for large expected frequencies) has the Chi-square distribution with the number of degrees of freedom calculated using the formula: 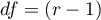 .
.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The settings window with the Chi-square test (goodness-of-fit) can be opened in Statistics menu → NonParametric tests (unordered categories)→Chi-square (goodnes-of-fit) or in ''Wizard''.
We would like to get to know if the number of dinners served in some school canteen within a given frame of time (from Monday to Friday) is statistically the same. To do this, there was taken a one-week-sample and written the number of served dinners in the particular days: Monday - 33, Tuesday - 29, Wednesday - 32, Thursday -36, Friday - 20.
As a result there were 150 dinners served in this canteen within a week (5 days).
We assume that the probability of serving dinner each day is exactly the same, so it comes to 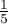 . The expected frequencies of served dinners for each day of the week (out of 5) comes to
. The expected frequencies of served dinners for each day of the week (out of 5) comes to 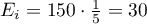 .
.
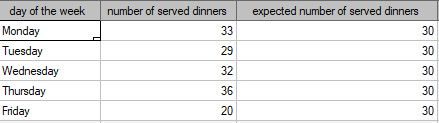
Hypotheses:

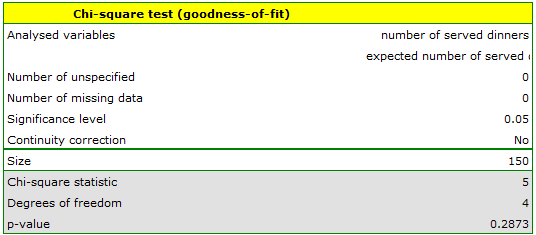
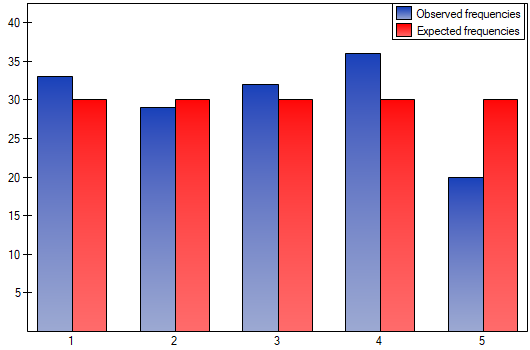
The p-value from the  distribution with 4 degrees of freedom comes to 0.2873. So using the significance level
distribution with 4 degrees of freedom comes to 0.2873. So using the significance level  you can estimate that there is no reason to reject the null hypothesis that informs about the compatibility of the number of served dinners with the expected number of dinners served within the particular days.
you can estimate that there is no reason to reject the null hypothesis that informs about the compatibility of the number of served dinners with the expected number of dinners served within the particular days.
Note!
If you want to make more comparisons within the framework of a one research, it is possible to use the Bonferroni correction7). The correction is used to limit the size of I type error, if we compare the observed frequencies and the expected ones between particular days, for example:
Friday  Monday,
Monday,
Friday  Tuesday,
Tuesday,
Friday  Wednesday,
Wednesday,
Friday  Thursday,
Thursday,
Provided that, the comparisons are made independently. The significance level  for each comparison must be calculated according to this correction using the following formula:
for each comparison must be calculated according to this correction using the following formula: 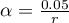 , where
, where 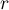 is the number of executed comparisons. The significance level for each comparison according to the Bonferroni correction (in this example) is
is the number of executed comparisons. The significance level for each comparison according to the Bonferroni correction (in this example) is 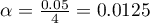 .
.
However, it is necessary to remember that if you reduce  for each comparison, the power of the test is increased.
for each comparison, the power of the test is increased.
Tests for one proportion
You should use tests for proportion if there are two possible results to obtain (one of them is an distinguished result with the size of m) and you know how often these results occur in the sample (we know a Z proportion). Depending on a sample size  you can choose the Z test for a one proportion – for large samples and the exact binomial test for a one proportion – for small sample sizes . These tests are used to verify the hypothesis that the proportion in the population, from which the sample is taken, is a given value.
you can choose the Z test for a one proportion – for large samples and the exact binomial test for a one proportion – for small sample sizes . These tests are used to verify the hypothesis that the proportion in the population, from which the sample is taken, is a given value.
Basic assumptions:
- measurement on a nominal scale - any order is not taken into account.
The additional condition for the Z test for proportion
- large frequencies (according to Marascuilo and McSweeney interpretation (1977)8) each of these values:
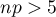 and
and 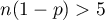 ).
).
Hypotheses:
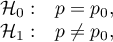
where:
 – probability (distinguished proportion) in the population,
– probability (distinguished proportion) in the population,
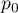 – expected probability (expected proportion).
– expected probability (expected proportion).
The Z test for one proportion
The test statistic is defined by:
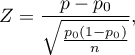
where:
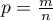 distinguished proportion for the sample taken from the population,
distinguished proportion for the sample taken from the population,
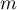 – frequency of values distinguished in the sample,
– frequency of values distinguished in the sample,
 – sample size.
– sample size.
The test statistic with a continuity correction is defined by:
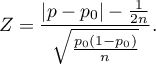
The  statistic with and without a continuity correction asymptotically (for large sizes) has the normal distribution.
statistic with and without a continuity correction asymptotically (for large sizes) has the normal distribution.
Binomial test for one proportion
The binomial test for one proportion uses directly the binomial distribution which is also called the Bernoulli distribution, which belongs to the group of discrete distributions (such distributions, where the analysed variable takes in the finite number of values). The analysed variable can take in 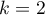 values. The first one is usually definited with the name of a success and the other one with the name of a failure. The probability of occurence of a success (distinguished probability) is
values. The first one is usually definited with the name of a success and the other one with the name of a failure. The probability of occurence of a success (distinguished probability) is 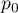 , and a failure
, and a failure 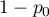 .
.
The probability for the specific point in this distribution is calculated using the formula:
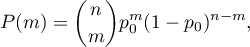
where:
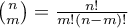 ,
,
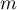 – frequency of values distinguished in the sample,
– frequency of values distinguished in the sample,
 – sample size.
– sample size.
Based on the total of appropriate probabilities  a one-sided and a two-sided p-value is calculated, and a two-sided
a one-sided and a two-sided p-value is calculated, and a two-sided  value is defined as a doubled value of the less of the one-sided probabilities.
value is defined as a doubled value of the less of the one-sided probabilities.
The p-value is compared with the significance level :
:

Note
Note that, for the estimator from the sample, which in this case is the value of the  proportion, a confidence interval is calculated. The interval for a large sample size can be based on the normal distribution - so-called Wald intervals. The more universal are intervals proposed by Wilson (1927)9) and by Agresti and Coull (1998)10). Clopper and Pearson (1934)11) intervals are more adequate for small sample sizes.
proportion, a confidence interval is calculated. The interval for a large sample size can be based on the normal distribution - so-called Wald intervals. The more universal are intervals proposed by Wilson (1927)9) and by Agresti and Coull (1998)10). Clopper and Pearson (1934)11) intervals are more adequate for small sample sizes.
Comparison of interval estimation methods of a binomial proportion was published by Brown L.D et al (2001)12)
The settings window with the Z test for one proportion can be opened in Statistics menu→NonParametric tests (unordered categories)→Z for proportion.
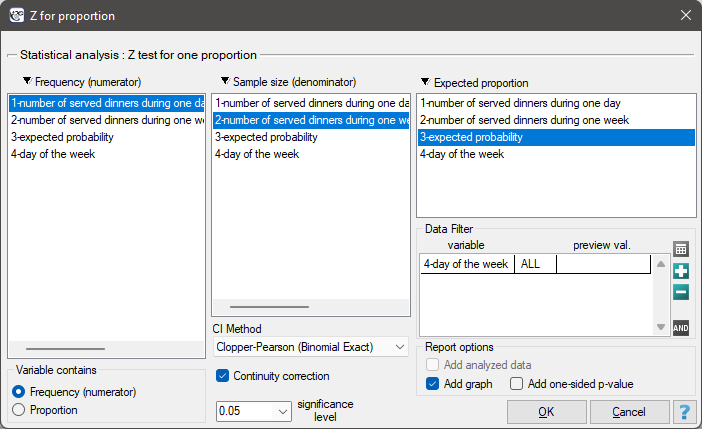
EXAMPLE cont. (dinners.pqs file)
Assume, that you would like to check if on Friday 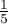 of all the dinners during the whole week are served. For the chosen sample
of all the dinners during the whole week are served. For the chosen sample  ,
,  .
.

Select the options of the analysis and activate a filter selecting the appropriate day of the week – Friday. If you do not activate the filter, no error will be generated, only statistics for given weekdays will be calculated.
Hypotheses:

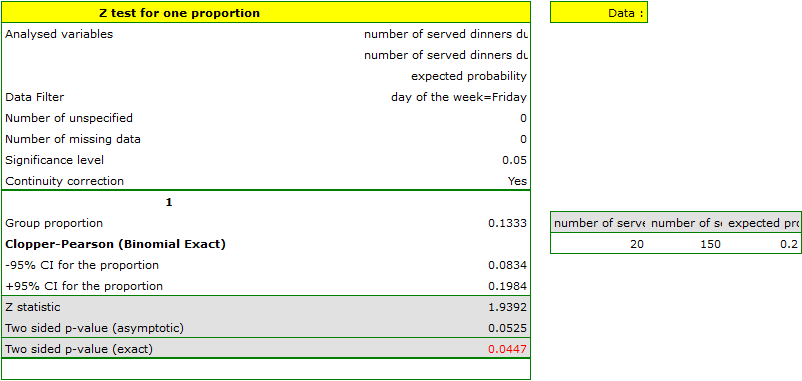
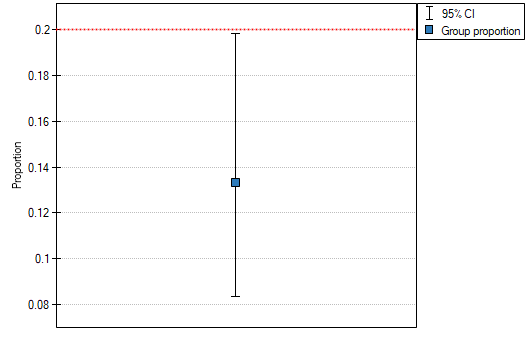
The proportion of the distinguished value in the sample is 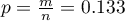 and 95% Clopper-Pearson confidence interval for this fraction
and 95% Clopper-Pearson confidence interval for this fraction 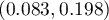 does not include the hypothetical value of 0.2.
does not include the hypothetical value of 0.2.
Based on the Z test without the continuity correction (p-value = 0.0412) and also on the basis of the exact value of the probability calculated from the binomial distribution (p-value = 0.0447) you can assume (on the significance level  ), that on Friday there are statistically less than
), that on Friday there are statistically less than 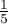 dinners served within a week. However, after using the continuity correction it is not possible to reject the null hypothesis p-value = 0.0525).
dinners served within a week. However, after using the continuity correction it is not possible to reject the null hypothesis p-value = 0.0525).