Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown1grpl:nparpl:wilcoxon1grpl
Test Wilcoxona (rangowanych znaków)
Test Wilcoxona rangowanych znaków (ang. Wilcoxon signed-ranks test) znany również pod nazwą testu Wilcoxona dla pojedynczej próby, Wilcoxon (1945, 1949)1). Test ten służy do weryfikacji hipotezy, że badana próba pochodzi z populacji, dla której mediana (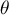 ) to znana wartość.
) to znana wartość.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej.
Hipotezy dotyczą równości sumy rang dodatnich i ujemnych lub są upraszczane do median:
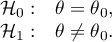
gdzie:
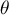 - mediana badanej cechy w populacji reprezentowanej przez badaną próbę,
- mediana badanej cechy w populacji reprezentowanej przez badaną próbę,
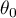 - zadana wartość.
- zadana wartość.
Wyznaczamy wartość statystyki testowej  (
(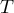 - dla małej liczności próby), a na jej podstawie wartość
- dla małej liczności próby), a na jej podstawie wartość  .
.
Porównujemy wartość  z poziomem istotności
z poziomem istotności  :
:
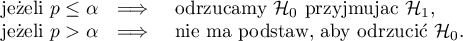
Uwaga!
W zależności od wielkości próby statystyka testowa przyjmuje inną postać:
- dla małej liczności próby
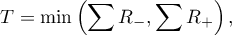
gdzie: 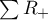 i
i 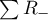 to odpowiednio: suma rang dodatnich i suma rang ujemnych.
to odpowiednio: suma rang dodatnich i suma rang ujemnych.
Statystyka ta podlega rozkładowi Wilcoxona
- dla próby o dużej liczności
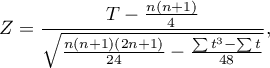
gdzie:  - liczba rangowanych znaków (liczba rang),
- liczba rangowanych znaków (liczba rang),
 - liczba przypadków wchodzących w skład rangi wiązanej.
- liczba przypadków wchodzących w skład rangi wiązanej.
Wzór na statystykę testową  zawiera poprawkę na rangi wiązane. Poprawka ta powinna być stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
zawiera poprawkę na rangi wiązane. Poprawka ta powinna być stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 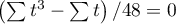 .
.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Poprawka na ciągłość testu Wilcoxona (Marascuilo and McSweeney (1977)2))
Poprawkę na ciągłość stosujemy by zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu normalnego. Wzór na statystykę testową z poprawką na ciągłość wyraża się wtedy wzorem:
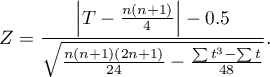
Standaryzowana wielkość efektu
Rozkład statystyki testu Wilcoxona jest aproksymowany przez rozkłady normalny, który można przekształcić na wielkość efektu 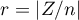 3) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
3) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
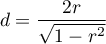
Przy interpretacji efektu badacze często posługują się ogólnymi, określonymi przez Cohena 4) wskazówkami definiującymi małą (0.2), średnią (0.5) i dużą (0.8) wielkość efektu.
Okno z ustawieniami opcji testu Wilcoxona (rangowanych znaków) wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Wilcoxon (rangowanych znaków) lub poprzez ''Kreator''.
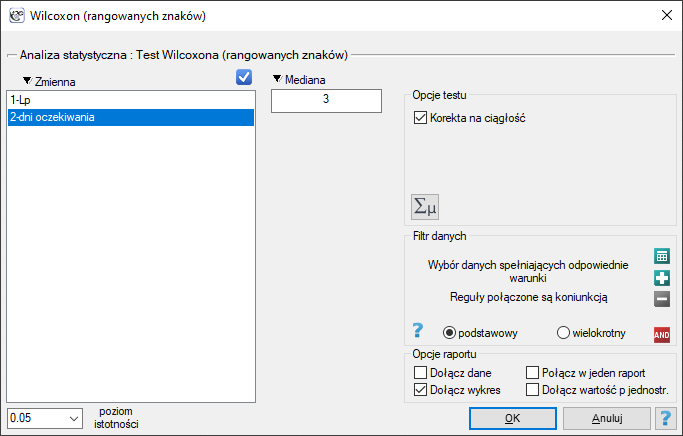
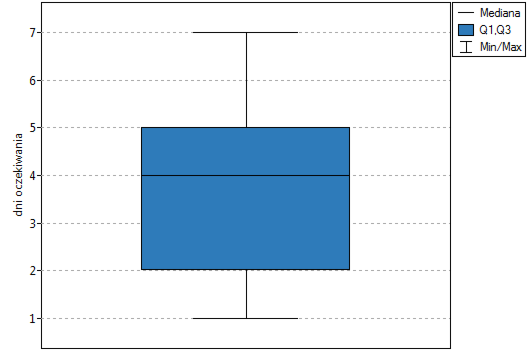
Przykład (plik kurier.pqs) c.d
Hipotezy:

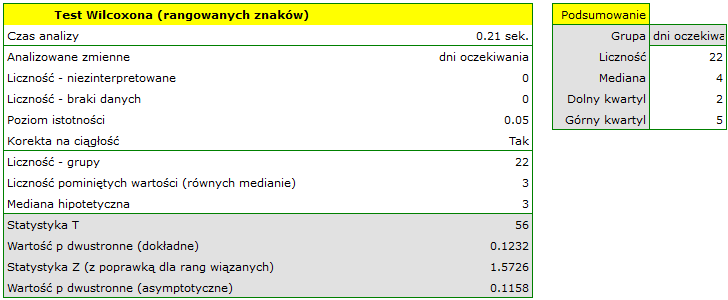
Porównując wartość 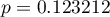 testu Wilcoxona opartego o statystykę
testu Wilcoxona opartego o statystykę 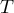 z poziomem istotności
z poziomem istotności  stwierdzamy, że nie mamy podstaw by odrzucić hipotezę zerową mówiącą, że zwykle liczba dni oczekiwania na dostarczenie przesyłki przez analizowaną firmę kurierską wynosi 3. Taką samą decyzję podjęlibyśmy również na podstawie wartości
stwierdzamy, że nie mamy podstaw by odrzucić hipotezę zerową mówiącą, że zwykle liczba dni oczekiwania na dostarczenie przesyłki przez analizowaną firmę kurierską wynosi 3. Taką samą decyzję podjęlibyśmy również na podstawie wartości 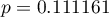 lub
lub 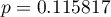 testu Wilcoxona opartego o statystykę
testu Wilcoxona opartego o statystykę  lub
lub  z poprawką na ciągłość.
z poprawką na ciągłość.
1)
Wilcoxon F. (1945), Individual comparisons by ranking methods. Biometries 1, 80-83
2)
Marascuilo L.A. and McSweeney M. (1977), Nonparametric and distribution-free method for the social sciences. Monterey, CA: Brooks Cole Publishing Company
3)
Fritz C.O., Morris P.E., Richler J.J.(2012), Effect size estimates: Current use, calculations, and interpretation. Journal of Experimental Psychology: General., 141(1):2–18.
4)
Cohen J. (1988), Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates, Hillsdale, New Jersey
statpqpl/porown1grpl/nparpl/wilcoxon1grpl.txt · ostatnio zmienione: 2022/09/14 09:05 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

