The Chi-square tests
These tests are based on data collected in the form of a contingency table of 2 traits, trait X and trait Y, the former having 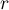 and the latter
and the latter 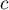 categories, so the resulting table has
categories, so the resulting table has 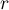 rows and
rows and 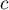 columns. Therefore, we can speak of the 2×2 chi-square test (for tables with two rows and two columns) or the RxC chi-square test (with multiple rows and columns)).
columns. Therefore, we can speak of the 2×2 chi-square test (for tables with two rows and two columns) or the RxC chi-square test (with multiple rows and columns)).
We can read the details of the chi-square test of the two features here:
Basic assumptions:
- measurement on a nominal scale - any order is not taken into account,
The additional assumption for the  :
:
General hypotheses:
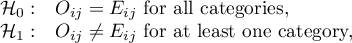
where:
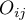 – observed frequencies in a contingency table,
– observed frequencies in a contingency table,
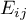 – expected frequencies in a contingency table.
– expected frequencies in a contingency table.
Hypotheses in the meaning of independence:

The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Additionally
- In addition to the chi-square test, another related test may need to be determined. In the event that Cochran's condition is not satisfied, one can determine:
- If we obtain a table of Rx2, and the R categories can be ordered, it is possible to determine the trend:
- When significant relationships or differences are found based on a test performed on a table larger than 2×2, then multiple comparisons can be performed with appropriate correction of the multiple comparisons to locate the location of these relationships/differences. This correction can be done automatically when the table has many columns. In such case, in test option window you should select
Multiple column comparisons (RxC). - In the case where we want to describe the strength of the relationship between feature X and feature Y, we can determine:
- In the case when we want to describe for 2×2 tables the effect size showing the impact of a risk factor, we can determine: