Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:warstwpl:mhpl:rrpl
Relatywne ryzyko Mantela-Haenszela
Jeśli wszystkie tabele (tworzone przez poszczególne warstwy) są homogeniczne (warunek ten można sprawdzić przy pomocy testu chi-kwadrat homogeniczności RR), wówczas na podstawie tych tabel można wyznaczyć wspólne relatywne ryzyko wraz z przedziałami ufności. Takie relatywne ryzyko jest średnią ważoną wartości Relatywnego Ryzyka wyznaczonego dla poszczególnych warstw. Zastosowanie ważonej metody zaproponowanej przez Mantela i Haenszela pozwala na uwzględnienie wkładu (wagi), jaki do budowy wspólnego Relatywnego Ryzyka wnosi każda warstwa (im bardziej liczna warstwa, tym większy ma wpływ na powstałe relatywne ryzyko).
Wagi dla każdej warstwy wyznacza się zgodnie z wzorem:
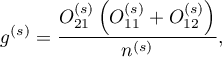
a relatywne ryzyko Mantela-Haenszela:
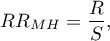
gdzie:
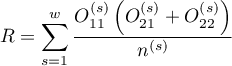 ,
,
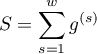 .
.
Przedział ufności dla 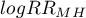 wyznacza się na podstawie błędu standardowego wyliczonego ze wzoru:
wyznacza się na podstawie błędu standardowego wyliczonego ze wzoru:
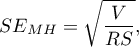
gdzie:
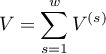 ,
,
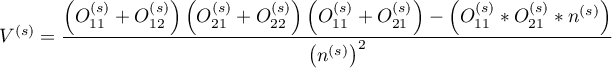 .
.
Test  Mantela-Haenszela (ang. Mantel-Haenszel Chi-square test) służy do weryfikacji hipotezy o istotności wyznaczonego Relatywnego Ryzyka (
Mantela-Haenszela (ang. Mantel-Haenszel Chi-square test) służy do weryfikacji hipotezy o istotności wyznaczonego Relatywnego Ryzyka (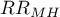 ) i powinien być wyliczany przy dużych licznościach w tabeli kontyngencji.
) i powinien być wyliczany przy dużych licznościach w tabeli kontyngencji.
Hipotezy:
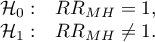
Statystyka testowa ma postać:
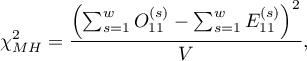
gdzie:
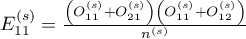 to wartości oczekiwane w pierwszej komórce tabeli kontyngencji, dla poszczególnych warstw
to wartości oczekiwane w pierwszej komórce tabeli kontyngencji, dla poszczególnych warstw 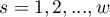 .
.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z jednym stopniem swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Test  homogeniczności dla
homogeniczności dla 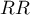 (ang. Chi-square test of homogeneity for RR) służy do weryfikacji hipotezy o tym, że zmienna tworząca warstwy jest efektem modyfikującym, tzn. wpływa ona na wyznaczane relatywne ryzyko w taki sposób, że jest on znacząco inne dla poszczególnych warstw.
(ang. Chi-square test of homogeneity for RR) służy do weryfikacji hipotezy o tym, że zmienna tworząca warstwy jest efektem modyfikującym, tzn. wpływa ona na wyznaczane relatywne ryzyko w taki sposób, że jest on znacząco inne dla poszczególnych warstw.
Hipotezy:
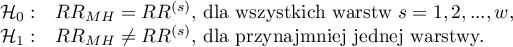
Statystyka testowa oparta o ważoną metodę najmniejszych kwadratów ma postać:
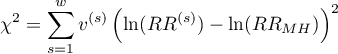
gdzie:
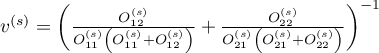 .
.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyliczaną według wzoru: 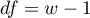 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

statpqpl/warstwpl/mhpl/rrpl.txt · ostatnio zmienione: 2014/08/23 00:19 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

