Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown3grpl:parpl:anova_repeatedcorrpl
ANOVA powtarzanych pomiarów z korektą Epsilon i MANOVA
Poprawki Epsilon i MANOVA dotyczą ANOVA powtarzanych pomiarów i są wyliczane wówczas, gdy nie jest spełnione założenie sferyczności lub wariancje różnic pomiędzy wszystkimi parami pomiarów nie są sobie bliskie.
Korekta braku sferyczności
Stopień w jakim sferyczność jest spełniona jest reprezentowany przez wartość  w teście Mauchly’a, ale również przez wartości Epsilon (
w teście Mauchly’a, ale również przez wartości Epsilon (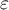 ) wyliczane wraz z korektami.
) wyliczane wraz z korektami. 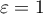 oznacza ścisłe przestrzeganie warunku sferyczności. Im mniejsza od 1 jest wartość Epsilon, tym założenie sferyczności jest bardziej naruszone. Dolna granica jaką Epsilon może osiągnąć to
oznacza ścisłe przestrzeganie warunku sferyczności. Im mniejsza od 1 jest wartość Epsilon, tym założenie sferyczności jest bardziej naruszone. Dolna granica jaką Epsilon może osiągnąć to 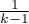 .
.
W celu zminimalizowania skutków braku sferyczności można wykorzystać trzy korekty zmieniające liczbę stopni swobody przy testowaniu z rozkładu F. Najprostszą lecz najsłabszą jest korekta dolnej granicy Epsilon. Nieco silniejszą lecz również konserwatywną jest korekta Greenhouse-Geisser (1959)1). Największą mocą charakteryzuje się korekta Huynh-Feldt (1976)2). Przy znacznym naruszeniu sferyczności najbardziej wskazanym rozwiązaniem jest jednak wykonanie analizy, która tego założenie nie wymaga, czyli MANOVA.
Podejście wielowymiarowe - MANOVA
MANOVA (ang. multivariate analysis of variance) czyli wielowymiarowa ANOVA jest analizą nie zakładającą sferyczności. W przypadku niespełnienia tego założenia jest to metoda najefektywniejsza, więc powinna być wybierana w zastępstwie analizy wariancji dla powtarzanych pomiarów. Omówienie tej metody można znaleźć w rozdziale jednoczynnikowa MANOVA. Zastosowanie jej do pomiarów powtarzanych (bez czynnika grup niezależnych) ogranicza jej działanie do danych będących różnicą sąsiadujących pomiarów i zapewnia testowanie tej samej hipotezy, co ANOVA dla zmiennych zależnych.
Okno z ustawieniami opcji jednoczynnikowej ANOVA dla grup zależnych z korektą Epsilon i MANOVA wywołujemy poprzez menu Statystyka→Testy parametryczne→ANOVA dla grup zależnych lub poprzez Kreator.
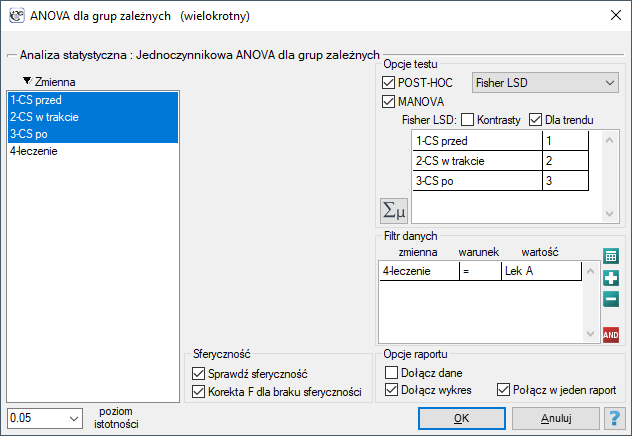
Badano skuteczność dwóch metod leczenia nadciśnienia. W tym celu zebrano próbę 56 chorych i przydzielono ich losowo do dwóch grup: grupy leczonej lekiem A i grupy leczonej lekiem B. Pomiaru ciśnienia skurczowego w każdej grupie dokonano trzykrotnie: przed leczeniem, w trakcie leczenia i po 6 miesiącach prowadzenia kuracji.
Hipotezy dla leczonych lekiem A:

Hipotezy dla leczonych lekiem B brzmią analogicznie.
Ponieważ dane mają rozkład normalny, analizę rozpoczynamy od sprawdzenia założenia o sferyczności. Testowanie wykonujemy dla każdej grupy osobno wykorzystując filtr wielokrotny.
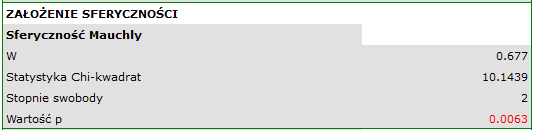
Na niespełnienie założenia sferyczności przez grupę leczoną lekiem B wskazują zarówno obserwowane wartości macierzy kowariancji i korelacji, jak i wynik testu Mauchly’a (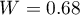 , wartość
, wartość 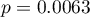 ).
).
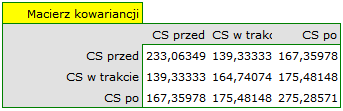
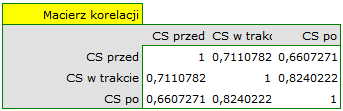
Wznawiamy analizę  i w oknie opcji testu wybieramy filtr podstawowy, by wykonać ANOVA powtarzanych pomiarów - dla leczonych lekiem A, a następnie korektę tej analizy i statystykę MANOVA - dla leczonych lekiem B.
i w oknie opcji testu wybieramy filtr podstawowy, by wykonać ANOVA powtarzanych pomiarów - dla leczonych lekiem A, a następnie korektę tej analizy i statystykę MANOVA - dla leczonych lekiem B.
Wyniki dla leczonych lekiem A:
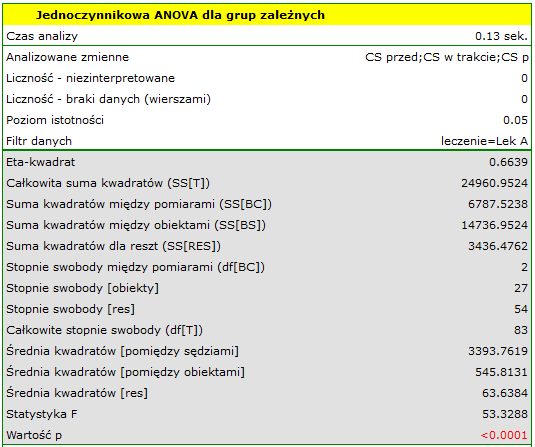
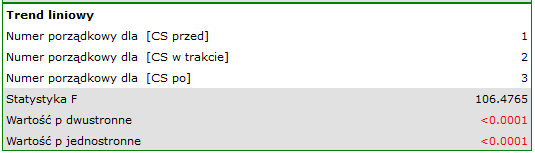
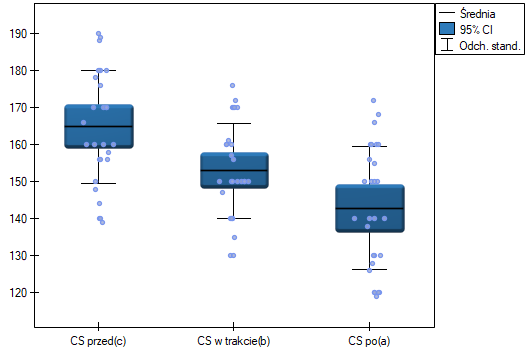
wskazują na istotne (na poziomie istotności  ) różnice pomiędzy średnimi wartościami ciśnienia skurczowego (wartość
) różnice pomiędzy średnimi wartościami ciśnienia skurczowego (wartość 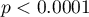 dla ANOVA powtarzanych pomiarów). Ponad 66% wewnątrzosobowego zróżnicowania wyników może być tłumaczona zastosowaniem leku A (
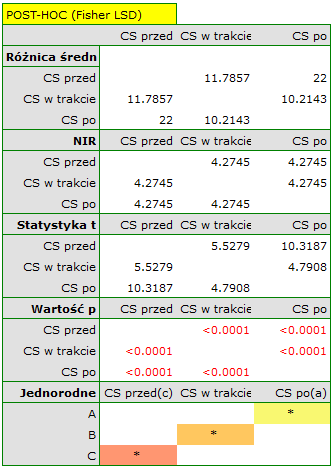
dla ANOVA powtarzanych pomiarów). Ponad 66% wewnątrzosobowego zróżnicowania wyników może być tłumaczona zastosowaniem leku A (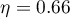 ). Różnice dotyczą wszystkich porównywanych etapów leczenia (wynik POST-HOC). Istotny jest również trend spadku ciśnienia skurczowego na skutek leczenia (wartość
). Różnice dotyczą wszystkich porównywanych etapów leczenia (wynik POST-HOC). Istotny jest również trend spadku ciśnienia skurczowego na skutek leczenia (wartość 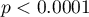 ). Zatem Lek A możemy uznać za lek skuteczny.
). Zatem Lek A możemy uznać za lek skuteczny.
Wyniki dla leczonych lekiem B:
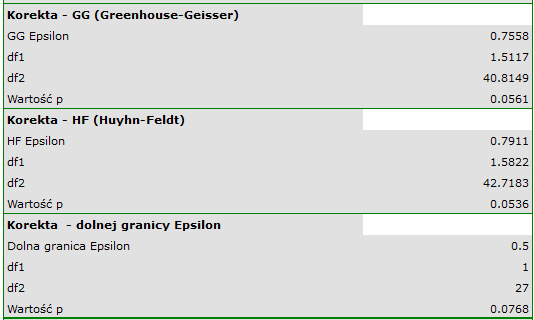
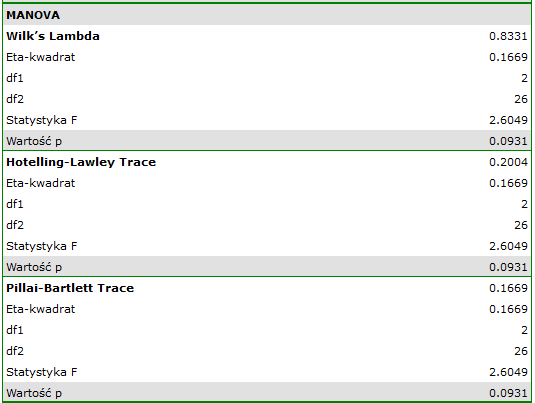
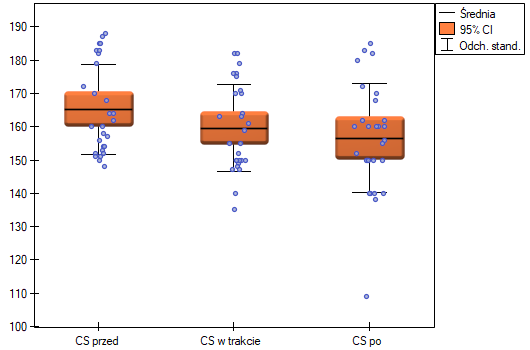
wskazują na brak istotnych różnic pomiędzy średnimi wartościami ciśnienia skurczowego, zarówno wtedy, gdy korzystamy z poprawek epsilon, jak i Lambda Wilksa (MANOVA). Zaledwie niecałe 17% wewnątrzosobowego zróżnicowania wyników może być tłumaczone zastosowaniem leku B (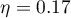 ).
).
1)
Greenhouse S. W., Geisser S. (1959), On methods in the analysis of profile data. Psychometrika, 24, 95–112
2)
Huynh H., Feldt L. S. (1976), Estimation of the Box correction for degrees of freedom from sample data in randomized block and split=plot designs. Journal of Educational Statistics, 1, 69–82
statpqpl/porown3grpl/parpl/anova_repeatedcorrpl.txt · ostatnio zmienione: 2022/11/20 18:07 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


