Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Porównanie - więcej niż 2 grupy » Testy parametryczne
Pasek boczny
statpqpl:porown3grpl:parpl
Spis treści
Testy parametryczne
ANOVA dla grup niezależnych
 Jednoczynnikowa analiza wariancji (ANOVA) dla grup niezależnych (ang. one-way analysis of variance) zaproponowana przez Ronalda Fishera, służy do weryfikacji hipotezy o równości średnich badanej zmiennej w kilku (
Jednoczynnikowa analiza wariancji (ANOVA) dla grup niezależnych (ang. one-way analysis of variance) zaproponowana przez Ronalda Fishera, służy do weryfikacji hipotezy o równości średnich badanej zmiennej w kilku (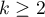 ) populacjach.
) populacjach.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu badanej zmiennej w każdej populacji,
- równość wariancji badanej zmiennej wszystkich populacji.
Hipotezy:
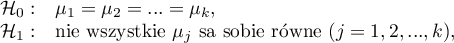
gdzie:
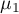 ,
,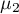 ,…,
,…,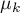
 średnie badanej zmiennej w populacjach, z których pobrano próby.
średnie badanej zmiennej w populacjach, z których pobrano próby.
Statystyka testowa ma postać:
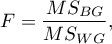
gdzie:
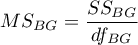 - średnia kwadratów między grupami,
- średnia kwadratów między grupami,
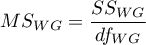 - średnia kwadratów wewnątrz grup,
- średnia kwadratów wewnątrz grup,
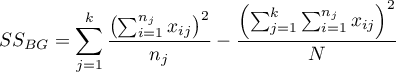 - suma kwadratów między grupami,
- suma kwadratów między grupami,
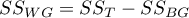 - suma kwadratów wewnątrz grup,
- suma kwadratów wewnątrz grup,
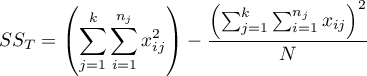 - całkowita suma kwadratów,
- całkowita suma kwadratów,
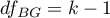 - stopnie swobody (między grupami),
- stopnie swobody (między grupami),
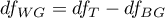 - stopnie swobody (wewnątrz grup),
- stopnie swobody (wewnątrz grup),
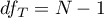 - całkowite stopnie swobody,
- całkowite stopnie swobody,
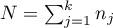 ,
,
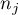 - liczności prób dla
- liczności prób dla  ,
,
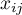 - wartości zmiennej w próbach dla
- wartości zmiennej w próbach dla 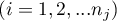 ,
,  .
.
Statystyka ta podlega rozkładowi F Snedecora z 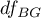 i
i 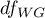 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Wielkość efektu - cząstkowa 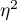
Wielkość ta określa proporcję wariancji wyjaśnionej do wariancji całkowitej związanej z danym czynnikiem. Zatem w modelu jednoczynnikowej ANOVA dla grup niezależnych wskazuje jaka część wewnątrzosobowej zmienności wyników może być przypisana badanemu czynnikowi wyznaczającemu grupy niezależne.
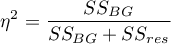
Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC
Okno z ustawieniami opcji jednoczynnikowej ANOVA dla grup niezależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→ANOVA dla grup niezależnych lub poprzez Kreator.
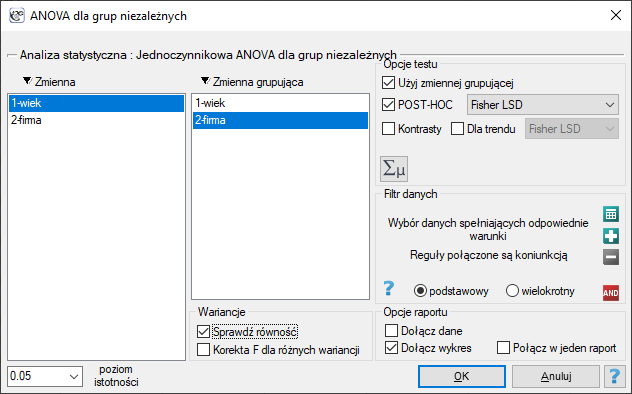
Przykład (plik wiek ANOVA.pqs)
W pewnym doświadczeniu bierze udział 150 osób wybranych w sposób losowy z populacji pracowników 3 różnych firm przewozowych. Z każdej firmy do próby wybrano 50 osób. Przed przystąpieniem do eksperymentu należy sprawdzić czy średni wiek pracowników tych firm jest podobny, od tego bowiem zależeć będzie kolejny etap eksperymentu. Wiek każdego uczestnika eksperymentu zapisano w latach.
Wiek (przewoźnik 1): 27, 33, 25, 32, 34, 38, 31, 34, 20, 30, 30, 27, 34, 32, 33, 25, 40, 35, 29, 20, 18, 28, 26, 22, 24, 24, 25, 28, 32, 32, 33, 32, 34, 27, 34, 27, 35, 28, 35, 34, 28, 29, 38, 26, 36, 31, 25, 35, 41, 37
Wiek (przewoźnik 2): 38, 34, 33, 27, 36, 20, 37, 40, 27, 26, 40, 44, 36, 32, 26, 34, 27, 31, 36, 36, 25, 40, 27, 30, 36, 29, 32, 41, 49, 24, 36, 38, 18, 33, 30, 28, 27, 26, 42, 34, 24, 32, 36, 30, 37, 34, 33, 30, 44, 29
Wiek (przewoźnik 3): 34, 36, 31, 37, 45, 39, 36, 34, 39, 27, 35, 33, 36, 28, 38, 25, 29, 26, 45, 28, 27, 32, 33, 30, 39, 40, 36, 33, 28, 32, 36, 39, 32, 39, 37, 35, 44, 34, 21, 42, 40, 32, 30, 23, 32, 34, 27, 39, 37, 35
Przed przystąpieniem do analizy ANOVA potwierdzono normalność rozkładu danych.
W oknie analizy sprawdzono założenie równości wariancji, uzyskując w obydwu testach p>0.05.
Hipotezy:
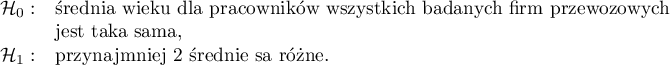
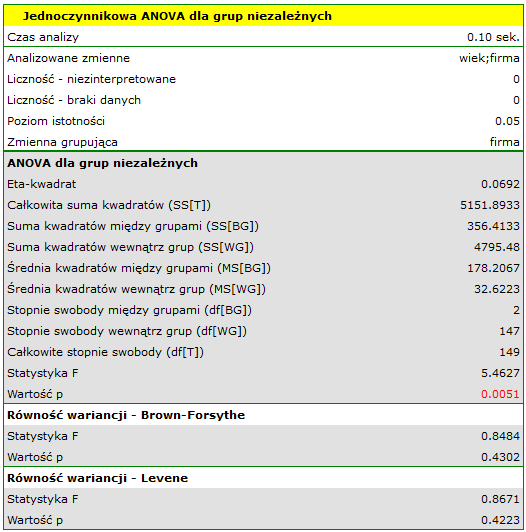
Porównując wartość 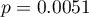 jednoczynnikowej analizy wariancji z poziomem istotności
jednoczynnikowej analizy wariancji z poziomem istotności  stwierdzamy, że średni wiek pracowników tych firm przewozowych jest różny. Na podstawie wyniku samej ANOVA nie możemy odpowiedzieć sobie na pytanie, które grupy różnią się pod względem wieku. By uzyskać taką wiedzę wykorzystany zostanie jeden z testów POST-HOC, np. test Tukeya. W tym celu {wznawiamy analizę} przyciskiem
stwierdzamy, że średni wiek pracowników tych firm przewozowych jest różny. Na podstawie wyniku samej ANOVA nie możemy odpowiedzieć sobie na pytanie, które grupy różnią się pod względem wieku. By uzyskać taką wiedzę wykorzystany zostanie jeden z testów POST-HOC, np. test Tukeya. W tym celu {wznawiamy analizę} przyciskiem  i w oknie opcji testu wybieramy
i w oknie opcji testu wybieramy Tukey HSD oraz dołączmy wykres.
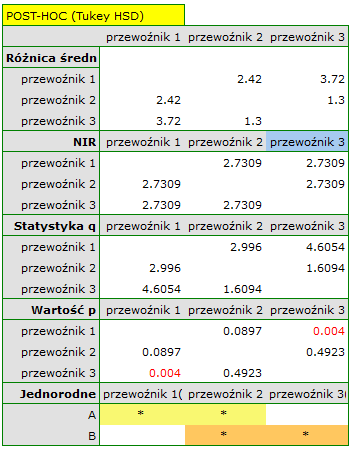
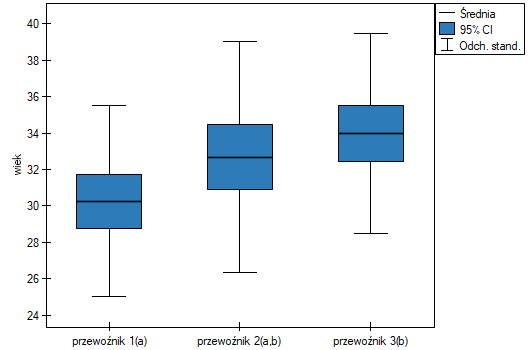
Najmniejsza istotna różnica (NIR) wyznaczona dla każdej pary porównań jest taka sama (ponieważ liczności grup są sobie równe) i wynosi 2.7309. Porównanie wartości NIR z wartością różnicy średnich wskazuje, że istotne różnice występują tylko pomiędzy wartością średnią dla wieku pracowników pierwszej i trzeciej firmy przewozowej (tylko w przypadku porównania tych dwóch grup wartość NIR jest mniejsza od różnicy średnich). Ten sam wniosek wyciągniemy porównując wartości  testu POST-HOC z poziomem istotności
testu POST-HOC z poziomem istotności  . Pracownicy pierwszej firmy są młodsi średnio o nieco ponad 3 lata od pracowników trzeciej firmy. Uzyskano dwie, zazębiające się grupy jednorodne, które zaznaczono również na wykresie.
. Pracownicy pierwszej firmy są młodsi średnio o nieco ponad 3 lata od pracowników trzeciej firmy. Uzyskano dwie, zazębiające się grupy jednorodne, które zaznaczono również na wykresie.
Dokładny opis danych możemy przedstawić wybierając w oknie analizy statystyki opisowe 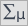
2014/08/22 20:00
Kontrasty i testy POST-HOC
Analiza wariancji daje informację tylko o tym, czy między populacjami występują istotne statystycznie różnice. Nie mówi ona, które populacje różnią się między sobą. By uzyskać wiedzę o różnicach dla fragmentu naszego złożonego układu stosujemy kontrasty (gdy dokonujemy wcześniej zaplanowanych i zwykle tylko wybranych porównań - tzw. a'priori), lub procedury porównań wielokrotnych czyli testy POST-HOC (gdy po wykonanej analizie wariancji szukamy różnic, zwykle pomiędzy wszystkimi parami).
Liczba wszystkich możliwych porównań prostych wyliczana jest z wzoru:
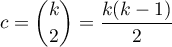
Hipotezy:
Przykład 1 - porównania proste (porównanie pomiędzy sobą 2 wybranych średnich):
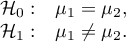
Przykład 2 - porównania złożone (porównanie kombinacji wybranych średnich):
![LaTeX \begin{array}{cc}
\mathcal{H}_0: & \mu_1=\frac{\mu_2+\mu_3}{2},\\[0.1cm]
\mathcal{H}_1: & \mu_1\neq\frac{\mu_2+\mu_3}{2}.
\end{array}](/lib/exe/fetch.php?media=wiki:latex:/imgf0472a7ad15f9b99bbf5ce50cb721339.png)
By można było zdefiniować wybrane hipotezy należy dla każdej średniej przypisać wartość kontrastu 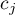 ,
,  . Wartości
. Wartości 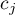 są tak wybierane by ich sumy dla porównywanych stron były liczbami przeciwnymi, a ich wartość dla średnich nie biorących udziału w analizie wynosi 0.
są tak wybierane by ich sumy dla porównywanych stron były liczbami przeciwnymi, a ich wartość dla średnich nie biorących udziału w analizie wynosi 0.
- Przykład 1:
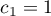 ,
,  ,
, 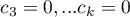 .
. - Przykład 2:
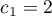 ,
,  ,
, 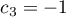 ,
, 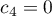 ,…,
,…, 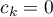 .
.
Wyboru właściwej hipotezy możemy dokonać:

 Porównując wyznaczoną na podstawie statystyki testowej odpowiedniego testu POST-HOC wartość
Porównując wyznaczoną na podstawie statystyki testowej odpowiedniego testu POST-HOC wartość  z poziomem istotności:
z poziomem istotności:

Dla porównań prostych i złożonych, zarówno równolicznych jak i różnolicznych grup, gdy wariancje nie różnią się istotnie.
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
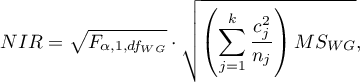
gdzie:
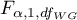 - to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności
- to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności  oraz dla stopni swobody odpowiednio: 1 i
oraz dla stopni swobody odpowiednio: 1 i 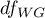 .
.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
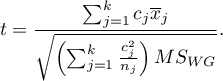
Statystyka ta podlega rozkładowi t-Studenta z 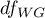 stopniami swobody.
stopniami swobody.
Dla porównań prostych zarówno równolicznych jak i różnolicznych grup, gdy wariancje nie różnią się istotnie.
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
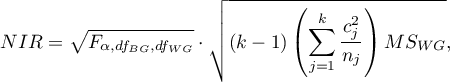
gdzie:
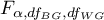 - to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności
- to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności  oraz
oraz 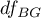 i
i 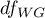 stopni swobody.
stopni swobody.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
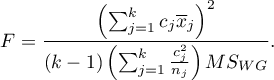
Statystyka ta podlega rozkładowi F Snedecora z 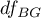 i
i 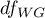 stopniami swobody.
stopniami swobody.
Dla porównań prostych zarówno równolicznych jak i różnolicznych grup, gdy wariancje nie różnią się istotnie.
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
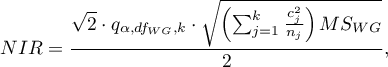
gdzie:
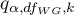 - to wartość krytyczna (statystyka) rozkładu studentyzowanego rozstępu dla zadanego poziomu istotności
- to wartość krytyczna (statystyka) rozkładu studentyzowanego rozstępu dla zadanego poziomu istotności  oraz
oraz 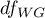 i
i  stopni swobody.
stopni swobody.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
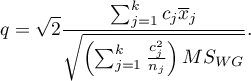
Statystyka ta podlega rozkładowi studentyzowanego rozstępu z  i
i  stopniami swobody.
stopniami swobody.
Info.
Algorytm obliczania wartości p i statystyki rozkładu studentyzowanego rozstępu w PQStat bazuje na pracy Lunda (1983)1). Inne programy lub strony internetowe mogą wyliczać nieco inne wartości niż PQStat, gdyż mogą bazować na mniej precyzyjnych lub bardziej restrykcyjnych algorytmach (Copenhaver i Holland (1988), Gleason (1999)).
Test badający istnienie trendu może być wyliczany w takiej samej sytuacji jak ANOVA dla zmiennych niezależnych, gdyż bazuje na tych samych założeniach, inaczej jednak ujmuje hipotezę alternatywną - wskazując w niej na istnienie trendu wartości średnich dla kolejnych populacji. Analiza trendu w ułożeniu średnich oparta jest na kontrastach LSD Fishera. Budując odpowiednie kontrasty można badać dowolny rodzaj trendu np. liniowy, kwadratowy, sześcienny, itd. Poniżej znajduje się tabela przykładowych wartości kontrastów dla wybranych trendów.
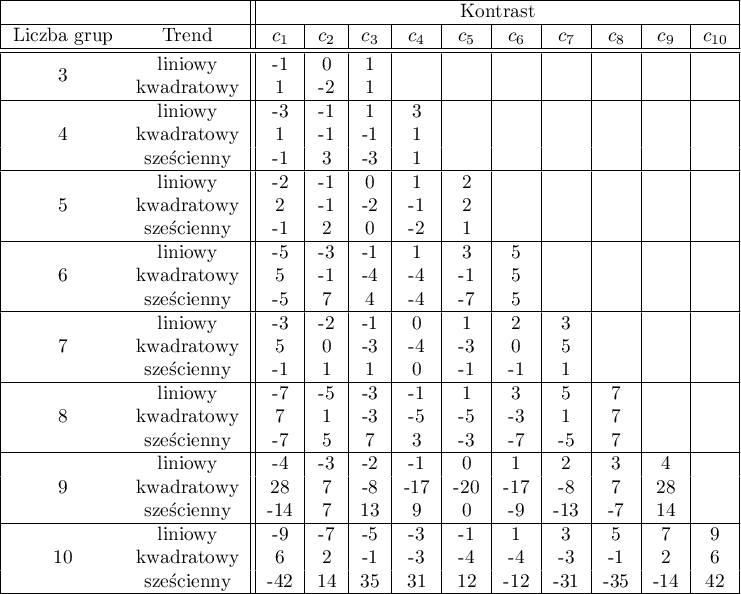
Trend liniowy
Trend liniowy, tak jak pozostałe trendy, możemy analizować wpisując odpowiednie wartości kontrastów. Jeśli jednak znany jest kierunek trendu liniowego, wystarczy skorzystać z opcji Trend liniowy i wskazać oczekiwaną kolejność populacji przypisując im kolejne liczby naturalne.
Analiza przeprowadzana jest w oparciu o kontrast liniowy, czyli wskazanym według naturalnego uporządkowania grupom przypisane są odpowiednie wartości kontrastu i wyliczona zostaje statystyka LSD Fishera.
Przy znanym oczekiwanym kierunku trendu, hipoteza alternatywna jest jednostronna i interpretacji podlega jednostronna wartość  . Interpretacja dwustronnej wartości
. Interpretacja dwustronnej wartości  oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość
oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Grupy jednorodne
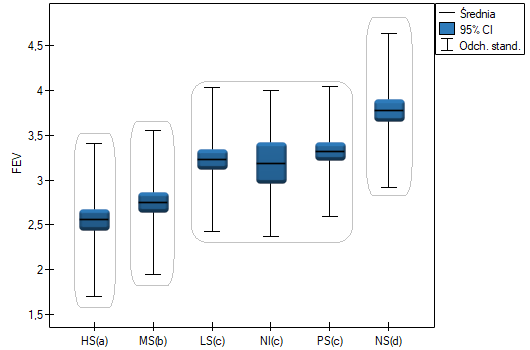
Dla każdego testu post-hoc, budowane są grupy jednorodne. Każda grupa jednorodna przedstawia zbiór grup, które nie różnią się od siebie w sposób istotny statystycznie. Na przykład, załóżmy, że podzieliliśmy badanych na sześć grup odnośnie statusu palenia: Nonsmokers (NS), Passive smokers (PS), Noninhaling smokers (NI), Light smokers (LS), Moderate smokers (MS), Heavy smokers (HS) i badamy dla nich parametry wydechowe. W przeprowadzonej analizie typu ANOVA uzyskaliśmy istotne statystycznie różnice w parametrach wydechowych pomiędzy badanymi grupami. Chcąc wskazać które grupy różnią się istotnie, a które nie, wykonujemy testy typu post-hoc. W rezultacie oprócz tabeli z wynikami poszczególnych par porównań i podanej istotności statystycznej w postaci wartości 
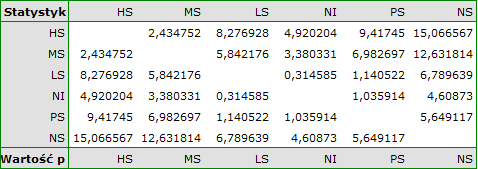
uzyskujemy podział na grupy jednorodne:
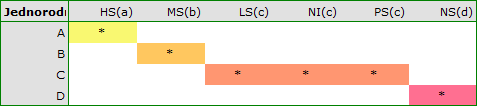
W tym przypadku uzyskano 4 grupy jednorodne tzn. A, B, C i D, co wskazuje na możliwość przeprowadzania badania w oparciu o mniejszy podział tzn. zamiast sześciu grup, które badaliśmy pierwotnie można prowadzić dalsze analizy w oparciu o cztery wyznaczone tu grupy jednorodne. Kolejność grup ustalona została na podstawie średnich ważonych wyliczonych dla poszczególnych grup jednorodnych, w taki sposób, by litera A przypisana została go grupy o najniższej średniej ważonej średniej ważonej, a dalsze litery alfabetu kolejno do grup o coraz wyższych średnich.
Okno z ustawieniami opcji jednoczynnikowej ANOVA dla grup niezależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→ANOVA dla grup niezależnych lub poprzez Kreator.

2014/08/22 20:00
ANOVA dla grup niezależnych z korektą F* i F''
 Poprawki
Poprawki 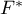 (Brown-Forsythe, 19742)) oraz
(Brown-Forsythe, 19742)) oraz 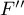 (Welch, 19513)) dotyczą ANOVA dla grup niezależnych i są wyliczane wówczas, gdy nie jest spełnione założenie równości wariancji.
(Welch, 19513)) dotyczą ANOVA dla grup niezależnych i są wyliczane wówczas, gdy nie jest spełnione założenie równości wariancji.
Statystyka testowa ma postać:
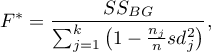
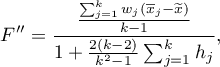
gdzie:
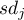
 odchylenie standardowe grupy
odchylenie standardowe grupy  ,
,
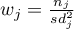
 waga grupy
waga grupy  ,
,
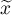
 średnia ważona,
średnia ważona,
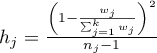 .
.
Statystyka ta podlega rozkładowi F Snedecora z 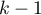 i skorygowanymi
i skorygowanymi 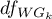 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC przeprowadzone zostało w rozdziale dotyczącym jednoczynnikowej analizy wariancji.
Dla porównań prostych i złożonych zarówno równolicznych jak i różnolicznych grup, gdy wariancje różnią się istotnie (Tamhane A. C., 19774)).
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
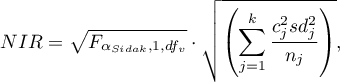
gdzie:
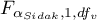 - to|wartość krytyczna (statystyka) rozkładu F Snedecora dla zmodyfikowanego poziomu istotności
- to|wartość krytyczna (statystyka) rozkładu F Snedecora dla zmodyfikowanego poziomu istotności 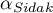 oraz dla stopni swobody 1 i
oraz dla stopni swobody 1 i 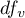 odpowiednio,
odpowiednio,
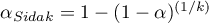 ,
,
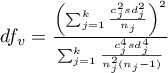
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
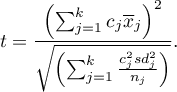
Statystyka ta podlega rozkładowi t-Studenta z 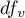 stopniami swobody, a wartość p jest korygowana o liczbę możliwych porównań prostych.
stopniami swobody, a wartość p jest korygowana o liczbę możliwych porównań prostych.
Test BF (Brown-Forsythe)
Dla porównań prostych zarówno równolicznych jak i różnolicznych grup, gdy wariancje różnią się istotnie (Brown M. B. i Forsythe A. B. (1974)5)).
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
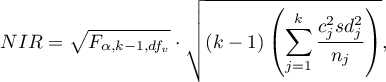
gdzie:
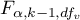 - to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności
- to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności  oraz
oraz 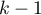 i
i 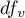 stopni swobody.
stopni swobody.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
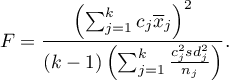
Statystyka ta podlega rozkładowi F Snedecora z 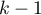 i
i 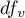 stopniami swobody.
stopniami swobody.
Test GH (Games-Howell).
Dla porównań prostych zarówno równolicznych jak i różnolicznych grup, gdy wariancje różnią się istotnie (Games P. A. i Howell J. F. 19766)).
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
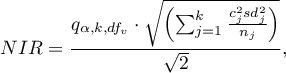
gdzie:
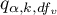 - to wartość krytyczna (statystyka) rozkładu studentyzowanego rozstępu dla zadanego poziomu istotności
- to wartość krytyczna (statystyka) rozkładu studentyzowanego rozstępu dla zadanego poziomu istotności  oraz
oraz  i
i 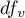 stopni swobody.
stopni swobody.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
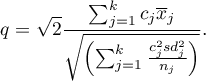
Statystyka ta podlega rozkładowi studentyzowanego rozstępu z  i
i 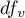 stopniami swobody.
stopniami swobody.
Test dla trendu.
Test badający istnienie trendu może być wyliczany w takiej samej sytuacji jak ANOVA dla grup niezależnych z korektą 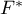 i
i 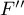 , gdyż bazuje na tych samych założeniach, inaczej jednak ujmuje hipotezę alternatywną - wskazując w niej na istnienie trendu wartości średnich dla kolejnych populacji. Analiza trendu w ułożeniu średnich oparta jest na kontrastach (T2 Tamhane). Budując odpowiednie kontrasty można badać dowolny rodzaj trendu np. liniowy, kwadratowy, sześcienny, itd. Tabela przykładowych wartości kontrastów dla wybranych trendów znajduje się w opisie testu dla trendu dla ANOVA bez korekty dla różnych wariancji.
, gdyż bazuje na tych samych założeniach, inaczej jednak ujmuje hipotezę alternatywną - wskazując w niej na istnienie trendu wartości średnich dla kolejnych populacji. Analiza trendu w ułożeniu średnich oparta jest na kontrastach (T2 Tamhane). Budując odpowiednie kontrasty można badać dowolny rodzaj trendu np. liniowy, kwadratowy, sześcienny, itd. Tabela przykładowych wartości kontrastów dla wybranych trendów znajduje się w opisie testu dla trendu dla ANOVA bez korekty dla różnych wariancji.
Trend liniowy
Trend liniowy, tak jak pozostałe trendy, możemy analizować wpisując odpowiednie wartości kontrastów. Jeśli jednak znany jest kierunek trendu liniowego, wystarczy skorzystać z opcji Trend liniowy i wskazać oczekiwaną kolejność populacji przypisując im kolejne liczby naturalne.
Analiza przeprowadzana jest w oparciu o kontrast liniowy, czyli wskazanym według naturalnego uporządkowania grupom przypisane są odpowiednie wartości kontrastu i wyliczona zostaje statystyka T2 Tamhane.
Przy znanym oczekiwanym kierunku trendu, hipoteza alternatywna jest jednostronna i interpretacji podlega jednostronna wartość  . Interpretacja dwustronnej wartości
. Interpretacja dwustronnej wartości  oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość
oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji jednoczynnikowej ANOVA dla grup niezależnych z korektą F* i F„ wywołujemy poprzez menu Statystyka→Testy parametryczne→ANOVA dla grup niezależnych lub poprzez Kreator.
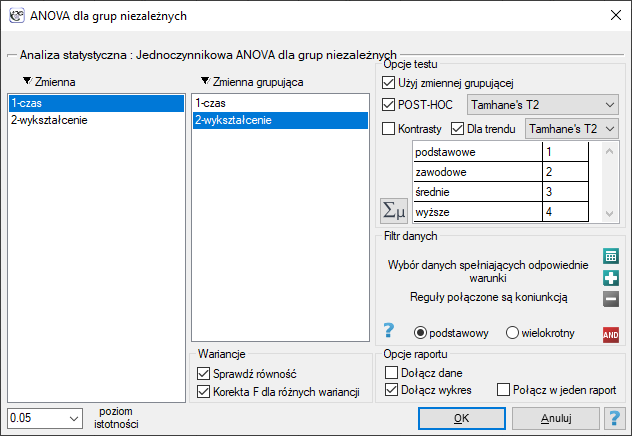
Przykład (plik bezrobocie.pqs)
Jest wiele czynników regulujących czas poszukiwania pracy w dobie kryzysu gospodarczego. Jednym z najważniejszych może być poziom wykształcenia. Przykładowe dane dotyczące wykształcenia oraz czasu (w miesiącach) pozostawania bezrobotnym zebrano w pliku. Chcemy sprawdzić czy istnieją różnice w średnim czasie poszukiwania pracy dla poszczególnych kategorii wykształcenia.
Hipotezy:

Ze względu na różnice dotyczące wariancji pomiędzy poszczególnymi populacjami (dla testu Levene wartość 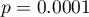 , a dla testu Brown-Forsythe wartość
, a dla testu Brown-Forsythe wartość 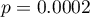 ):
):

analizę przeprowadzamy przy włączonej korekcie różnych wariancji. Uzyskany wynik skorygowanej statystyki  jest przedstawiony poniżej.
jest przedstawiony poniżej.
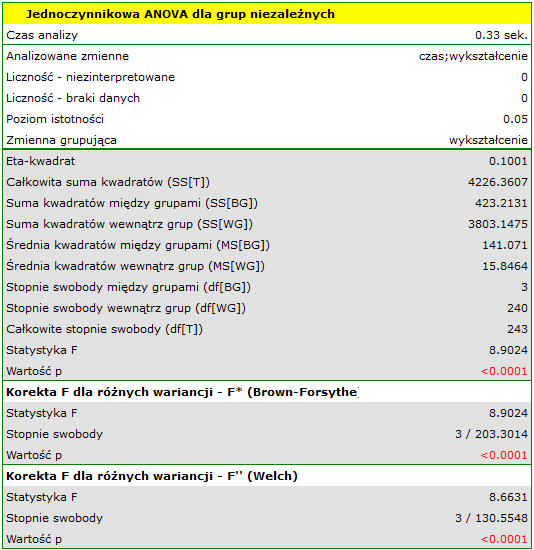
Porównując wartość 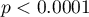 (dla testu
(dla testu 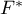 ) oraz wartość
) oraz wartość 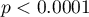 (dla testu
(dla testu 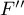 ) z poziomem istotności
) z poziomem istotności  stwierdzamy, że średni czas poszukiwania pracy różni się w zależności od posiadanego wykształcenia. Wykonując jeden z testów POST-HOC, dedykowany porównaniu grup o różnych wariancjach, dowiadujemy się których kategorii wykształcenia dotyczą stwierdzone różnice:
stwierdzamy, że średni czas poszukiwania pracy różni się w zależności od posiadanego wykształcenia. Wykonując jeden z testów POST-HOC, dedykowany porównaniu grup o różnych wariancjach, dowiadujemy się których kategorii wykształcenia dotyczą stwierdzone różnice:
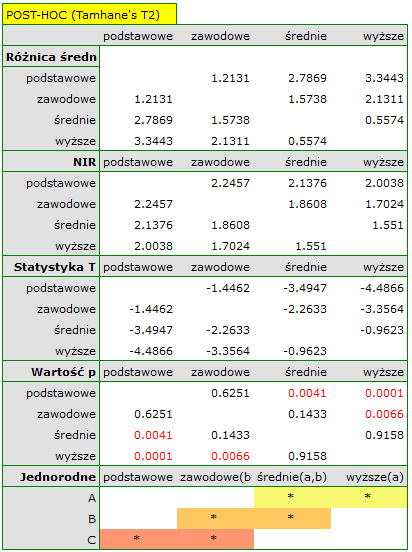
Najmniejsza istotna różnica (NIR) wyznaczona dla każdej pary porównań nie jest taka sama (mimo, że liczności grup są sobie równe), ponieważ nie są równe wariancje. Odnosząc wartość NIR do uzyskanych różnic wartości średnich uzyskamy ten sam rezultat co porównując wartość  z poziomem istotności
z poziomem istotności  . Różnice dotyczą wykształcenia podstawowego i wyższego, wykształcenia podstawowego i średniego oraz wykształcenia zawodowego i wyższego. Powstałe grupy jednorodne zazębiają się. Generalnie jednak, spoglądając na wykres, możemy oczekiwać, że czym bardziej wykształcona osoba, tym mniej czasu zajmuje jej poszukiwanie pracy.
. Różnice dotyczą wykształcenia podstawowego i wyższego, wykształcenia podstawowego i średniego oraz wykształcenia zawodowego i wyższego. Powstałe grupy jednorodne zazębiają się. Generalnie jednak, spoglądając na wykres, możemy oczekiwać, że czym bardziej wykształcona osoba, tym mniej czasu zajmuje jej poszukiwanie pracy.
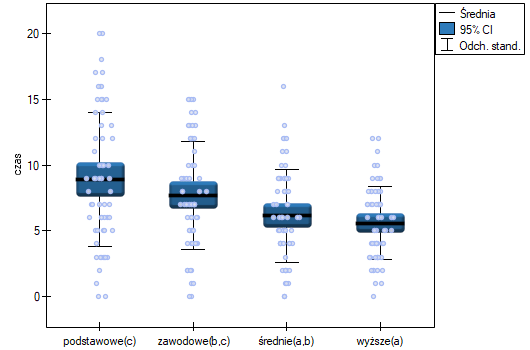
By móc sprawdzić tak postawioną hipotezę, należy podjąć analizę dla trendu. W tym celu {wznawiamy analizę} przyciskiem  i w oknie opcji testu wybieramy: metodę
i w oknie opcji testu wybieramy: metodę Tamhane's T2, opcję Kontrasy (i ustawiamy odpowiedni kontrast) lub opcję Dla trendu (i wskazujemy kolejność kategorii wykształcenia podając kolejne liczby naturalne).
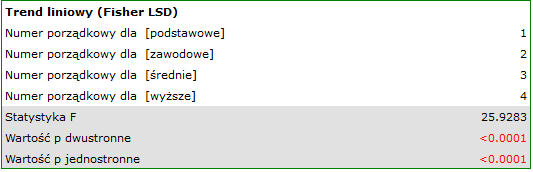
W zależności od tego czy kierunek zależności pomiędzy wykształceniem a czasem poszukiwania pracy jest nam znany, wykorzystujemy jednostronną lub dwustronną wartość  . Obie te wartości są mniejsze niż zadany poziom istotności. Przewidywany przez nas trend został potwierdzony, czyli na poziomie istotności
. Obie te wartości są mniejsze niż zadany poziom istotności. Przewidywany przez nas trend został potwierdzony, czyli na poziomie istotności  możemy powiedzieć, że ów trend istnieje rzeczywiście w populacji z której pochodzi próba.
możemy powiedzieć, że ów trend istnieje rzeczywiście w populacji z której pochodzi próba.
2014/12/18 00:41
· admin
Test Browna-Forsythea i Levenea
Obydwa testy: test Levenea (ang. Levene test), Levene (1960)7) i test Browna-Forsythea (ang. Brown-Forsythe test), Brown i Forsythe (1974)8), służą do weryfikacji hipotezy o równości wariancji badanej zmiennej w kilku (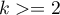 ) populacjach.
) populacjach.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu badanej zmiennej w każdej populacji,
Hipotezy:
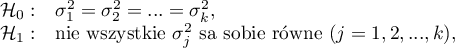
gdzie:
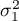 ,
,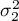 ,…,
,…,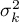 - wariancje badanej zmiennej w populacjach, z których pobrano próby.
- wariancje badanej zmiennej w populacjach, z których pobrano próby.
Analiza polega na wyznaczaniu bezwzględnego odchylenia wyników pomiarowych od średniej (w teście Levenea) lub od mediany (w teście Browna-Forsythea), w każdej z badanych grup. Owo bezwzględne odchylenie stanowi dane, które zostają poddane dokładnie tej samej procedurze, którą wykonuje się dla analizy wariancji dla grup niezależnych. Stąd statystyka testowa przyjmuje postać:
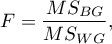
Statystyka ta podlega rozkładowi F Snedecora z 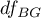 i
i 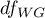 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
Test Browna-Forsythea jest mniej wrażliwy niż test Levenea na niespełnienie założenia dotyczącego normalności rozkładu.
Okno z ustawieniami opcji testu Levenea, Browna-Forsythea wywołujemy poprzez menu Statystyka→Testy parametryczne→Levene, Brown-Forsythe.
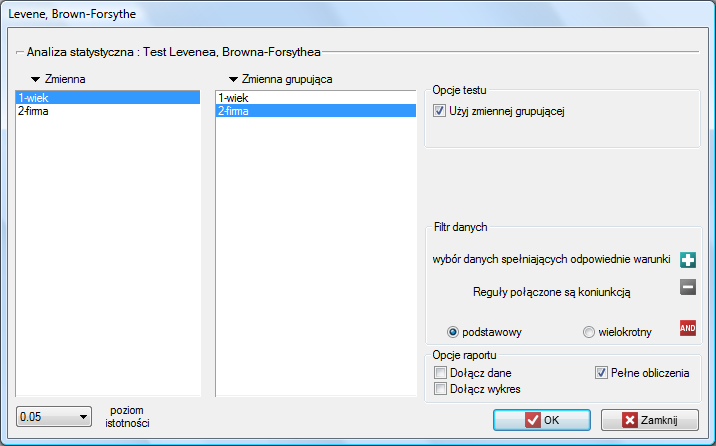
2014/08/22 20:00
ANOVA powtarzanych pomiarów
Jednoczynnikowa analiza wariancji dla powtarzanych pomiarów, czyli ANOVA dla grup zależnych (ang. single-factor repeated-measures analysis of variance) stosuje się w sytuacji, gdy pomiarów badanej zmiennej dokonujemy kilkukrotnie (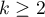 ) w różnych warunkach (przy czym zakładamy, że wariancje różnic pomiędzy wszystkimi parami pomiarów są sobie bliskie).
) w różnych warunkach (przy czym zakładamy, że wariancje różnic pomiędzy wszystkimi parami pomiarów są sobie bliskie).
Test ten służy do weryfikacji hipotezy o równości średnich badanej zmiennej w kilku (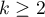 ) populacjach.
) populacjach.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu dla wszystkich zmiennych będących różnicą par pomiarowych (lub normalność badanej zmiennej dla każdego pomiaru),
Hipotezy:
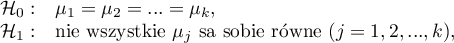
gdzie:
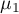 ,
,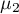 ,…,
,…,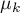 - średnie badanej zmiennej w kolejnych pomiarach z badanej populacji.
- średnie badanej zmiennej w kolejnych pomiarach z badanej populacji.
Statystyka testowa ma postać:
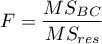
gdzie:
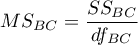 -średnia kwadratów między pomiarami,
-średnia kwadratów między pomiarami,
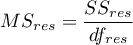 - średnia kwadratów dla reszt,
- średnia kwadratów dla reszt,
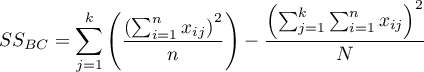 - suma kwadratów między pomiarami,
- suma kwadratów między pomiarami,
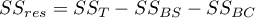 - suma kwadratów dla reszt,
- suma kwadratów dla reszt,
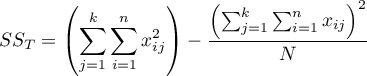 - całkowita suma kwadratów,
- całkowita suma kwadratów,
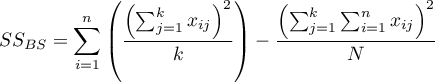 - suma kwadratów między obiektami,
- suma kwadratów między obiektami,
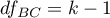 - stopnie swobody (między pomiarami),
- stopnie swobody (między pomiarami),
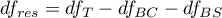 - stopnie swobody (dla reszt),
- stopnie swobody (dla reszt),
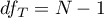 - całkowite stopnie swobody,
- całkowite stopnie swobody,
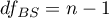 - stopnie swobody (między obiektami),
- stopnie swobody (między obiektami),
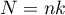 ,
,
 - liczność próby,
- liczność próby,
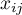 - wartości zmiennej dla
- wartości zmiennej dla  obiektów
obiektów 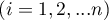 w
w  pomiarach
pomiarach  .
.
Statystyka ta podlega rozkładowi F Snedecora z 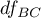 i
i 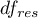 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Wielkość efektu - cząstkowa 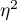
Wielkość ta określa proporcję wariancji wyjaśnionej do wariancji całkowitej związanej z danym czynnikiem. Zatem w modelu powtarzanych pomiarów wskazuje jaka część wewnątrzosobowej zmienności wyników może być przypisana powtarzanym pomiarom zmiennej.
Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC przeprowadzone zostało w rozdziale dotyczącym jednoczynnikowej analizy wariancji.
Dla porównań prostych i złożonych (liczność w poszczególnych pomiarach zawsze jest taka sama).
Hipotezy:
Przykład - porównania proste (porównanie pomiędzy sobą 2 wybranych średnich):
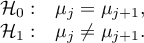
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
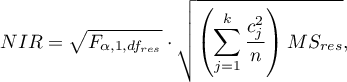
gdzie:
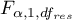 - to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności
- to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności  oraz dla stopni swobody odpowiednio: 1 i
oraz dla stopni swobody odpowiednio: 1 i 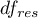 .
.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
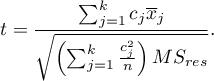
Statystyka ta podlega rozkładowi t-Studenta z 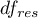 stopniami swobody.
stopniami swobody.
Uwaga!
Dla kontrastów wielkość 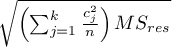 zastąpiona jest błędem kontrastu
zastąpiona jest błędem kontrastu 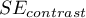 , a stopnie swobody to
, a stopnie swobody to 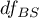 .
.
Dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:

gdzie:
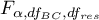 - to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności
- to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności  oraz
oraz 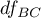 i
i 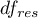 stopni swobody.
stopni swobody.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
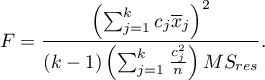
Statystyka ta podlega rozkładowi F Snedecora z 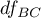 i
i 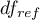 stopniami swobody.
stopniami swobody.
Dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
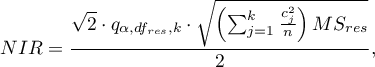
gdzie:
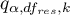 - to wartość krytyczna (statystyka) rozkładu studentyzowanego rozstępu dla zadanego poziomu istotności
- to wartość krytyczna (statystyka) rozkładu studentyzowanego rozstępu dla zadanego poziomu istotności  oraz
oraz 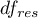 i
i  stopni swobody.
stopni swobody.
 ] Statystyka testowa ma postać:
] Statystyka testowa ma postać:
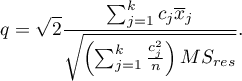
Statystyka ta podlega rozkładowi studentyzowanego rozstępu 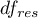 i
i  stopniami swobody.
stopniami swobody.
Info.
Algorytm obliczania wartości p i statystyki rozkładu studentyzowanego rozstępu w PQStat bazuje na pracy Lunda (1983)9). Inne programy lub strony internetowe mogą wyliczać nieco inne wartości niż PQStat, gdyż mogą bazować na mniej precyzyjnych lub bardziej restrykcyjnych algorytmach (Copenhaver i Holland (1988), Gleason (1999)).
Test dla trendu.
Test badający istnienie trendu może być wyliczany w takiej samej sytuacji jak ANOVA dla zmiennych zależnych, gdyż bazuje na tych samych założeniach, inaczej jednak ujmuje hipotezę alternatywną - wskazując w niej na istnienie trendu wartości średnich w kolejnych pomiarach. Analiza trendu w ułożeniu średnich oparta jest na kontrastach Test LSD Fishera. Budując odpowiednie kontrasty można badać dowolny rodzaj trendu np. liniowy, kwadratowy, sześcienny, itd. Tabela przykładowych wartości kontrastów dla wybranych trendów znajduje się w opisie testu dla trendu dla ANOVA zmiennych niezależnych.
Trend liniowy
Trend liniowy, tak jak pozostałe trendy, możemy analizować wpisując odpowiednie wartości kontrastów. Jeśli jednak znany jest kierunek trendu liniowego, wystarczy skorzystać z opcji Trend liniowy i wskazać oczekiwaną kolejność populacji przypisując im kolejne liczby naturalne.
Analiza przeprowadzana jest w oparciu o kontrast liniowy, czyli wskazanym według naturalnego uporządkowania grupom przypisane są odpowiednie wartości kontrastu i wyliczona zostaje statystyka Test LSD Fishera.
Przy znanym oczekiwanym kierunku trendu, hipoteza alternatywna jest jednostronna i interpretacji podlega jednostronna wartość  . Interpretacja dwustronnej wartości
. Interpretacja dwustronnej wartości  oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość
oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji jednoczynnikowej ANOVA dla grup zależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→ANOVA dla grup zależnych lub poprzez Kreator.
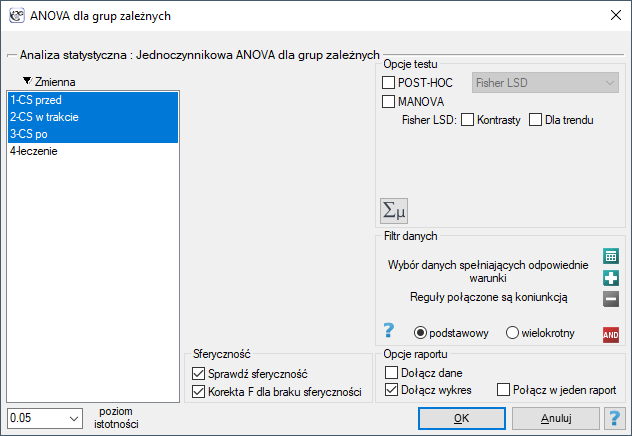
Patrz przykład (plik ciśnienie.pqs)
2014/08/22 20:00
ANOVA powtarzanych pomiarów z korektą Epsilon i MANOVA
Poprawki Epsilon i MANOVA dotyczą ANOVA powtarzanych pomiarów i są wyliczane wówczas, gdy nie jest spełnione założenie sferyczności lub wariancje różnic pomiędzy wszystkimi parami pomiarów nie są sobie bliskie.
Korekta braku sferyczności
Stopień w jakim sferyczność jest spełniona jest reprezentowany przez wartość  w teście Mauchly’a, ale również przez wartości Epsilon (
w teście Mauchly’a, ale również przez wartości Epsilon (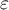 ) wyliczane wraz z korektami.
) wyliczane wraz z korektami. 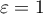 oznacza ścisłe przestrzeganie warunku sferyczności. Im mniejsza od 1 jest wartość Epsilon, tym założenie sferyczności jest bardziej naruszone. Dolna granica jaką Epsilon może osiągnąć to
oznacza ścisłe przestrzeganie warunku sferyczności. Im mniejsza od 1 jest wartość Epsilon, tym założenie sferyczności jest bardziej naruszone. Dolna granica jaką Epsilon może osiągnąć to 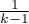 .
.
W celu zminimalizowania skutków braku sferyczności można wykorzystać trzy korekty zmieniające liczbę stopni swobody przy testowaniu z rozkładu F. Najprostszą lecz najsłabszą jest korekta dolnej granicy Epsilon. Nieco silniejszą lecz również konserwatywną jest korekta Greenhouse-Geisser (1959)10). Największą mocą charakteryzuje się korekta Huynh-Feldt (1976)11). Przy znacznym naruszeniu sferyczności najbardziej wskazanym rozwiązaniem jest jednak wykonanie analizy, która tego założenie nie wymaga, czyli MANOVA.
Podejście wielowymiarowe - MANOVA
MANOVA (ang. multivariate analysis of variance) czyli wielowymiarowa ANOVA jest analizą nie zakładającą sferyczności. W przypadku niespełnienia tego założenia jest to metoda najefektywniejsza, więc powinna być wybierana w zastępstwie analizy wariancji dla powtarzanych pomiarów. Omówienie tej metody można znaleźć w rozdziale jednoczynnikowa MANOVA. Zastosowanie jej do pomiarów powtarzanych (bez czynnika grup niezależnych) ogranicza jej działanie do danych będących różnicą sąsiadujących pomiarów i zapewnia testowanie tej samej hipotezy, co ANOVA dla zmiennych zależnych.
Okno z ustawieniami opcji jednoczynnikowej ANOVA dla grup zależnych z korektą Epsilon i MANOVA wywołujemy poprzez menu Statystyka→Testy parametryczne→ANOVA dla grup zależnych lub poprzez Kreator.
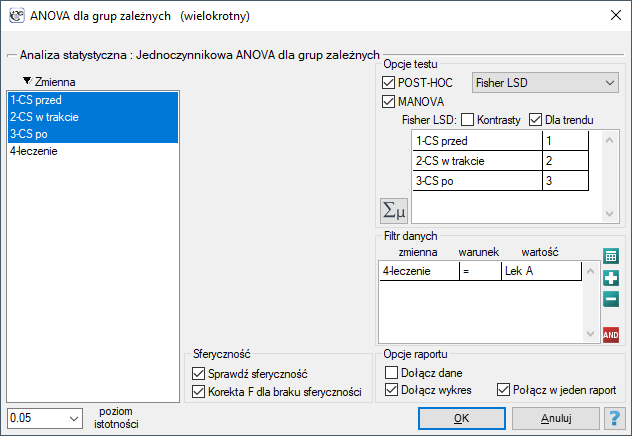
Badano skuteczność dwóch metod leczenia nadciśnienia. W tym celu zebrano próbę 56 chorych i przydzielono ich losowo do dwóch grup: grupy leczonej lekiem A i grupy leczonej lekiem B. Pomiaru ciśnienia skurczowego w każdej grupie dokonano trzykrotnie: przed leczeniem, w trakcie leczenia i po 6 miesiącach prowadzenia kuracji.
Hipotezy dla leczonych lekiem A:

Hipotezy dla leczonych lekiem B brzmią analogicznie.
Ponieważ dane mają rozkład normalny, analizę rozpoczynamy od sprawdzenia założenia o sferyczności. Testowanie wykonujemy dla każdej grupy osobno wykorzystując filtr wielokrotny.
Na niespełnienie założenia sferyczności przez grupę leczoną lekiem B wskazują zarówno obserwowane wartości macierzy kowariancji i korelacji, jak i wynik testu Mauchly’a (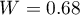 , wartość
, wartość 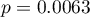 ).
).
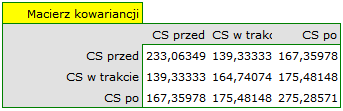
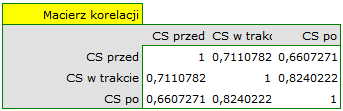
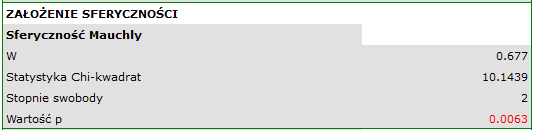
Wznawiamy analizę  i w oknie opcji testu wybieramy filtr podstawowy, by wykonać ANOVA powtarzanych pomiarów - dla leczonych lekiem A, a następnie korektę tej analizy i statystykę MANOVA - dla leczonych lekiem B.
i w oknie opcji testu wybieramy filtr podstawowy, by wykonać ANOVA powtarzanych pomiarów - dla leczonych lekiem A, a następnie korektę tej analizy i statystykę MANOVA - dla leczonych lekiem B.
Wyniki dla leczonych lekiem A:
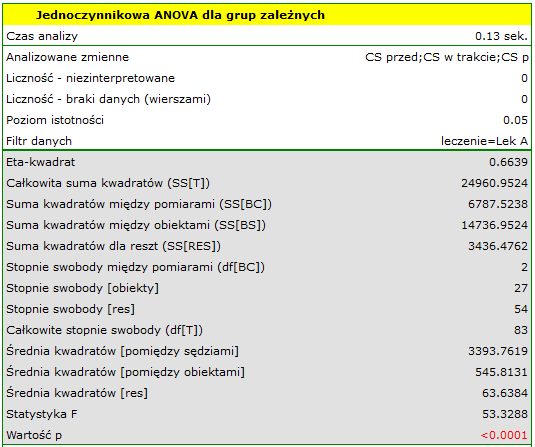
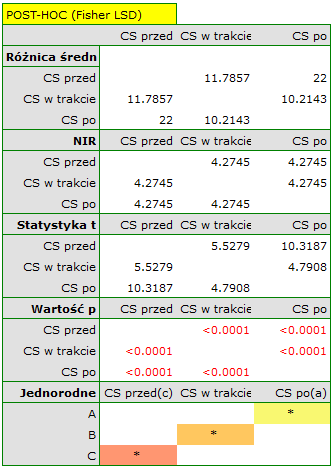
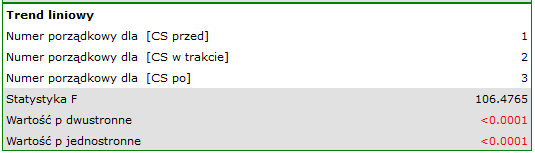
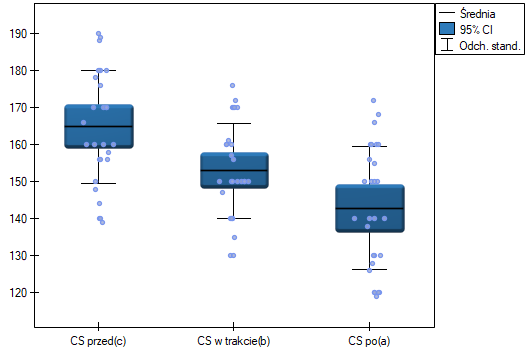
wskazują na istotne (na poziomie istotności  ) różnice pomiędzy średnimi wartościami ciśnienia skurczowego (wartość
) różnice pomiędzy średnimi wartościami ciśnienia skurczowego (wartość 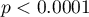 dla ANOVA powtarzanych pomiarów). Ponad 66% wewnątrzosobowego zróżnicowania wyników może być tłumaczona zastosowaniem leku A (
dla ANOVA powtarzanych pomiarów). Ponad 66% wewnątrzosobowego zróżnicowania wyników może być tłumaczona zastosowaniem leku A (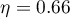 ). Różnice dotyczą wszystkich porównywanych etapów leczenia (wynik POST-HOC). Istotny jest również trend spadku ciśnienia skurczowego na skutek leczenia (wartość
). Różnice dotyczą wszystkich porównywanych etapów leczenia (wynik POST-HOC). Istotny jest również trend spadku ciśnienia skurczowego na skutek leczenia (wartość 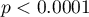 ). Zatem Lek A możemy uznać za lek skuteczny.
). Zatem Lek A możemy uznać za lek skuteczny.
Wyniki dla leczonych lekiem B:
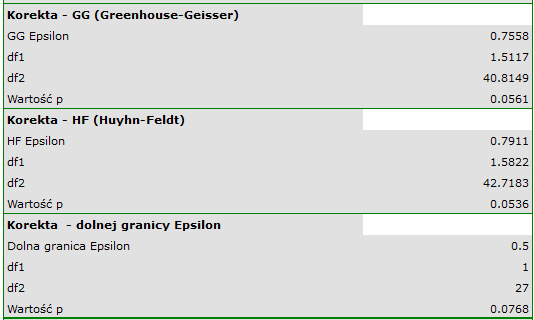
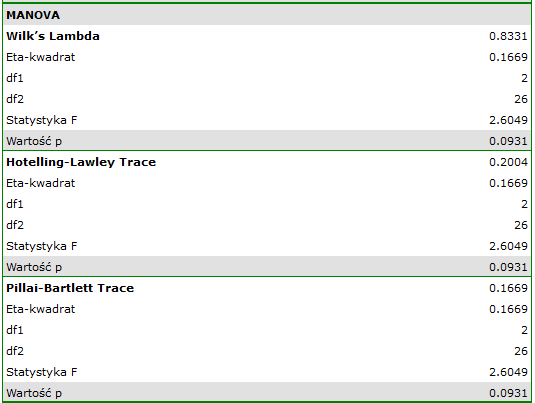
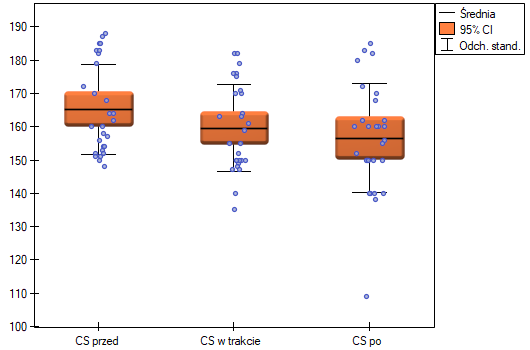
wskazują na brak istotnych różnic pomiędzy średnimi wartościami ciśnienia skurczowego, zarówno wtedy, gdy korzystamy z poprawek epsilon, jak i Lambda Wilksa (MANOVA). Zaledwie niecałe 17% wewnątrzosobowego zróżnicowania wyników może być tłumaczone zastosowaniem leku B (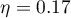 ).
).
2014/12/18 16:03
· admin
Sferyczność Mauchly’a
Założenie sferyczności jest podobne ale silniejsze niż założenie równości wariancji. Jest ono spełnione, jeśli wariancje dla różnic pomiędzy parami powtarzanych pomiarów są takie same. Zwykle w zastępstwie założenia o sferyczności rozważa się prostszy, ale bardziej rygorystyczny warunek symetrii połączonej (ang. compound symmetry). Można tak postąpić ponieważ spełnienie warunku symetrii połączonej pociąga za sobą spełnienie założenia sferyczności.
Warunek symetrii połączonej zakłada symetrię w macierzy kowariancji, a zatem równość wariancji zmiennych (elementów głównej przekątnej macierzy kowariancji) oraz równość kowariancji (elementów poza główną przekątną macierzy kowariancji).
Naruszenie założenia sferyczności lub symetrii połączonej zmniejsza w nieuzasadniony sposób konserwatyzm testu F (ułatwia odrzucenie hipotezy zerowej).
Dla sprawdzenia założenia sferyczności używa się testu Mauchly’a (1940)12). Istotność wyniku (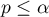 ) oznacza tu naruszenie założenia sferyczności.
) oznacza tu naruszenie założenia sferyczności.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- wielowymiarowy rozkład normalny lub normalność rozkładu każdej badanej zmiennej,
Hipotezy:
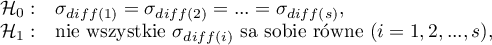
gdzie:
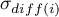 - populacyjna wariancja różnic pomiędzy
- populacyjna wariancja różnic pomiędzy  -tą parą powtarzanych pomiarów,
-tą parą powtarzanych pomiarów,
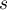 - liczba par.
- liczba par.
Wartość  Mauchly’a definiowana jest następująco:
Mauchly’a definiowana jest następująco:
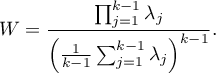
Statystyka testowa ma postać:
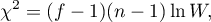
gdzie:
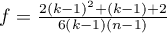 ,
,
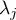 - wartość własna oczekiwanej macierzy kowariancji,
- wartość własna oczekiwanej macierzy kowariancji,
 - liczba analizowanych zmiennych.
- liczba analizowanych zmiennych.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 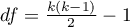 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Wartość 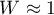 oznacza spełnienie założenia sferyczności. W interpretacji wyników tego testu należy jednak pamiętać, że jest on wrażliwy na złamanie założenia normalności rozkładu.
oznacza spełnienie założenia sferyczności. W interpretacji wyników tego testu należy jednak pamiętać, że jest on wrażliwy na złamanie założenia normalności rozkładu.
Patrz przykład (plik ciśnienie.pqs)
2014/12/18 15:58
· admin
1)
, 9)
Lund R.E., Lund J.R. (1983), Algorithm AS 190, Probabilities and Upper Quantiles for the Studentized Range. Applied Statistics; 34
2)
Brown M. B., Forsythe A. B. (1974), The small sample behavior of some statistics which test the equality of several means. Technometrics, 16, 385-389
3)
Welch B. L. (1951), On the comparison of several mean values: an alternative approach. Biometrika 38: 330–336
4)
Tamhane A. C. (1977), Multiple comparisons in model I One-Way ANOVA with unequal variances. Communications in Statistics, A6 (1), 15-32
5)
Brown M. B., Forsythe A. B. (1974), The ANOVA and multiple comparisons for data with heterogeneous variances. Biometrics, 30, 719-724
6)
Games P. A., Howell J. F. (1976), Pairwise multiple comparison procedures with unequal n's and/or variances: A Monte Carlo study. Journal of Educational Statistics, 1, 113-125
7)
Levene H. (1960), Robust tests for the equality of variance. In I. Olkin (Ed.) Contributions to probability and statistics (278-292). Palo Alto, CA: Stanford University Press
8)
Brown M.B., Forsythe A. B. (1974a), Robust tests for equality of variances. Journal of the American Statistical Association, 69,364-367
10)
Greenhouse S. W., Geisser S. (1959), On methods in the analysis of profile data. Psychometrika, 24, 95–112
11)
Huynh H., Feldt L. S. (1976), Estimation of the Box correction for degrees of freedom from sample data in randomized block and split=plot designs. Journal of Educational Statistics, 1, 69–82
12)
Mauchly J. W. (1940), Significance test for sphericity of n-variate normal population. Annals of Mathematical Statistics, 11, 204-209
statpqpl/porown3grpl/parpl.txt · ostatnio zmienione: 2014/12/20 17:12 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

