Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown2grpl:nparpl:fishercxrpl
Test Fishera dla tabel dużych tabel
Test Fishera dla tabel 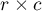 zwany jest również testem Fishera-Freemana-Haltona (ang. Fisher-Freeman-Halton test), Freeman G.H., Halton J.H. (1951)1). Test ten jest rozszerzeniem na tabele
zwany jest również testem Fishera-Freemana-Haltona (ang. Fisher-Freeman-Halton test), Freeman G.H., Halton J.H. (1951)1). Test ten jest rozszerzeniem na tabele 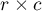 testu dokładnego Fishera. Określa dokładne prawdopodobieństwo wystąpienia konkretnego rozkładu liczb w tabeli przy znanym
testu dokładnego Fishera. Określa dokładne prawdopodobieństwo wystąpienia konkretnego rozkładu liczb w tabeli przy znanym  i ustalonych sumach brzegowych.
i ustalonych sumach brzegowych.
Jeśli sumy brzegowe wierszy zdefiniujemy jako:
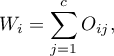
gdzie:
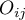
 liczności obserwowane w tabeli kontyngencji,
liczności obserwowane w tabeli kontyngencji,
a sumy brzegowe kolumn jako:
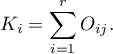
To przy ustalonych sumach brzegowych, dla różnych układów wartości obserwowanych oznaczonych jako 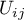 wyznaczamy prawdopodobieństwa
wyznaczamy prawdopodobieństwa 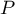 :
:
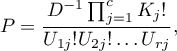
gdzie
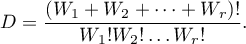
Dokładny poziom istotności  jest sumą tych prawdopodobieństw
jest sumą tych prawdopodobieństw 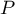 (wyznaczonych dla nowych wartości
(wyznaczonych dla nowych wartości 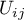 ), które są mniejsze lub równe prawdopodobieństwu
), które są mniejsze lub równe prawdopodobieństwu 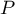 tabeli z wartościami początkowymi
tabeli z wartościami początkowymi 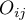
Porównujemy dokładną wartość  z poziomem istotności
z poziomem istotności  :.
:.
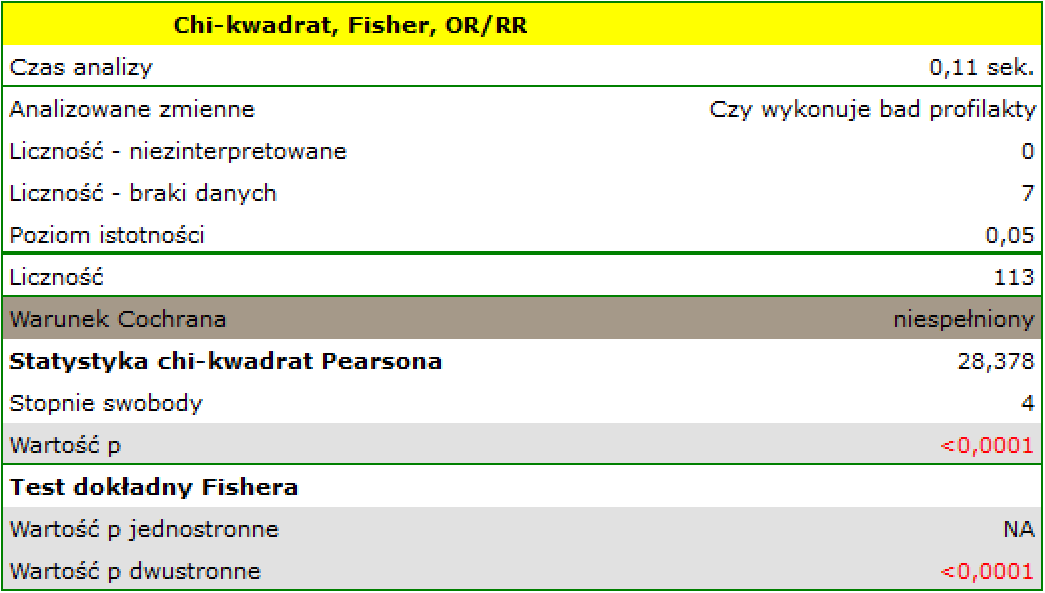
Okno z ustawieniami opcji testu dokładny Fishera (RxC) wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Chi-kwadrat, Fisher OR/RR lub poprzez ''Kreator''.
Info.
Procedura obliczania wartości  dla tego testu bazuje na algorytmie opublikowanym w pracy Mehta (1986)2).
dla tego testu bazuje na algorytmie opublikowanym w pracy Mehta (1986)2).
Przykład (plik praca-profilaktyka.pqs)
W populacji osób zamieszkujących na obszarach wiejskich gminy Komorniki badano czy wykonywanie badań profilaktyki zdrowia jest uzależnione od rodzaju aktywność zawodowej mieszkańców. Zebrano losową próbę 120 osób i zapytano o wykształcenie oraz o to czy osoby te wykonują badania profilaktyczne. Pełną odpowiedź uzyskano od 113 osób.
dane_praca_profilaktyka
Hipotezy:

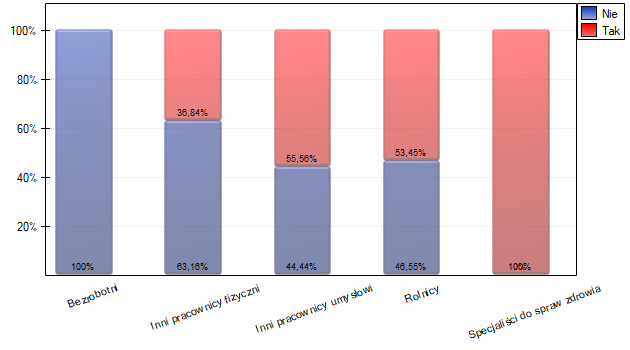
Warunek Cochrana nie jest spełniony, przez co nie powinniśmy stosować testu chi-kwadrat.
Wartość 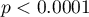 . Zatem na poziomie istotności
. Zatem na poziomie istotności  możemy powiedzieć, że istniej zależność pomiędzy wykonywaniem badań profilaktycznych a rodzajem wykonywanej pracy przez mieszkańców obszarów wiejskich gminy Komorniki.
możemy powiedzieć, że istniej zależność pomiędzy wykonywaniem badań profilaktycznych a rodzajem wykonywanej pracy przez mieszkańców obszarów wiejskich gminy Komorniki.
Jeśli interesują nas dokładniejsze informacje na temat wykrytych zależności, uzyskamy je wyznaczając porównania wielokrotne poprzez opcje Fisher, Yates i inne… a następnie Wielokrotne porównania kolumn (RxC) i jedną z poprawek np. Benjamini-Hochberg
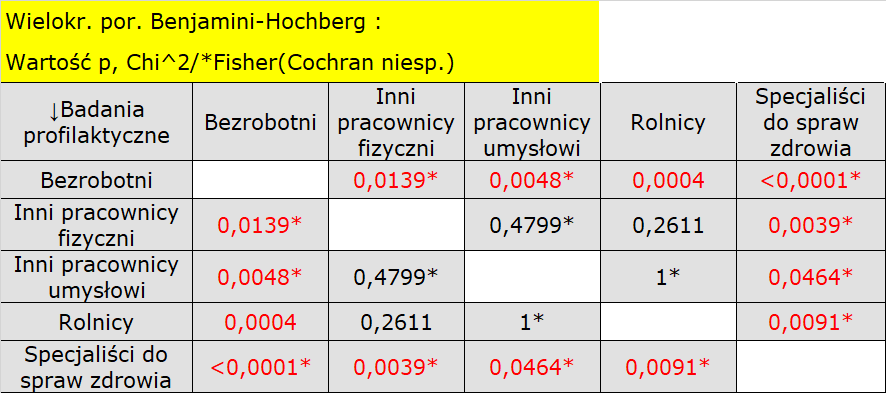
Dokładniejsza analiza pozwala stwierdzić, że specjaliści do spraw zdrowia istotnie częściej niż pozostałe grupy wykonują badania profilaktyczne (100% osób w tej grupie wykonało badania), a bezrobotni istotnie rzadziej (nikt w tej grupie nie wykonał badania). Rolnicy, inni pracownicy fizyczni i inni pracownicy umysłowi w około 50% wykonują badania profilaktyczne co powoduje, że te trzy grupy nie różnią się od siebie istotnie statystycznie. Część wartości p uzyskanych w tabeli oznaczona jest gwiazdką, oznacza ona te wyniki które powstały poprzez użycie testu dokładnego Fishera wraz z poprawką Benjaminiego-Hochberga, wartości nie oznaczone są wynikiem testu chi-kwadrat wraz z poprawką Benjaminiego-Hochberga, przy którym założenia Cochrana były spełnione
1)
Freeman G.H. and Halton J.H. (1951), Note on an exact treatment of contingency, goodness of fit and other problems of significance. Biometrika 38:141-149
2)
Mehta C.R. and Patel N.R. (1986), Algorithm 643. FEXACT: A Fortran subroutine for Fisher's exact test on unordered r*c contingency tables. ACM Transactions on Mathematical Software, 12, 154–161
statpqpl/porown2grpl/nparpl/fishercxrpl.txt · ostatnio zmienione: 2022/01/23 21:16 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

