Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
pl:statpqpl:rzetelnpl
Analiza rzetelności
Analiza rzetelności (ang. reliability analysis) związana jest najczęściej z budową skal złożonych, w szczególności skal sumarycznych, czyli składających się z wielu pojedynczych pozycji (pytań). Rzetelność skali - rozumiana jako jej wewnętrzna spójność, daje nam informację o tym, na ile dana skala mierzy to, co mierzy; czyli w jakim stopniu poszczególne pozycje skali mierzą to, co cała skala.
Aby można było mówić o rzetelności skali, poszczególne pozycje skali powinny mierzyć ten sam konstrukt - korelacja pomiędzy poszczególnymi pozycjami skali powinna być wysoka. Założenie to możemy sprawdzić wyliczając macierz współczynników korelacji Pearsona. Pomimo, że w zagadnieniu rzetelności mogą być wykorzystywane różne miary zgodności, najczęściej używaną techniką jest tutaj współczynnik  -Cronbacha i tzw. rzetelność połówkowa.
-Cronbacha i tzw. rzetelność połówkowa.
Alfa Cronbacha i rzetelność połówkowa
Współczynnik  -Cronbacha (ang. Cronbach's alpha) został tak nazwany po raz pierwszy przez Cronbacha w 19511). Mierzy on stosunek wariancji poszczególnych pozycji do wariancji całej skali (sumy tych pozycji) i jest wyliczany ze wzoru:
-Cronbacha (ang. Cronbach's alpha) został tak nazwany po raz pierwszy przez Cronbacha w 19511). Mierzy on stosunek wariancji poszczególnych pozycji do wariancji całej skali (sumy tych pozycji) i jest wyliczany ze wzoru:
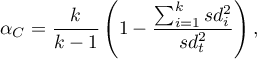
gdzie:
 - liczba pozycji w skali,
- liczba pozycji w skali,
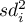 - wariancja pozycji
- wariancja pozycji  ,
,
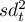 - wariancja sumy wszystkich pozycji.
- wariancja sumy wszystkich pozycji.
Standaryzowany współczynnik rzetelności 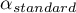 jest wyliczany jako:
jest wyliczany jako:
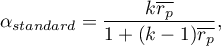
gdzie:
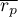 -średnia współczynników korelacji Pearsona wszystkich (
-średnia współczynników korelacji Pearsona wszystkich (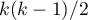 ) pozycji skali.
) pozycji skali.
Współczynnik  może przyjmować dowolne wartości mniejsze lub równe 1, w tym również wartości ujemne, jednakże tylko wartości dodatnie mają sens. Jeżeli wszystkie pozycje skali są idealnie rzetelne, wówczas współczynnik rzetelności wynosi 1.
może przyjmować dowolne wartości mniejsze lub równe 1, w tym również wartości ujemne, jednakże tylko wartości dodatnie mają sens. Jeżeli wszystkie pozycje skali są idealnie rzetelne, wówczas współczynnik rzetelności wynosi 1.
Pomocą w ocenie przydatności konkretnych pozycji skali służą:
- wartość współczynnika
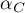 obliczonego po usunięciu określonej pozycji skali,
obliczonego po usunięciu określonej pozycji skali,
- wartość odchylenia standardowego skali obliczonego po usunięciu określonej pozycji skali,
- wartość średnia skali obliczona po usunięciu określonej pozycji skali,
- wartość korelacji określonej pozycji i sumy pozycji pozostałych.
Rzetelność połówkowa (ang. split-half reliability)
Polega na losowym podzieleniu pozycji skali na dwie połowy i analizie korelacji między tymi połówkami. Odbywa się to przy użyciu współczynnika rzetelności połówkowej Spearmana-Browna opublikowanego niezależnie przez Spearmana (1910)2) i Browna (1910)3):
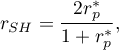
gdzie:
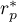
 współczynnik korelacji Pearsona pomiędzy połówkami skali.
współczynnik korelacji Pearsona pomiędzy połówkami skali.
Jeżeli dwie losowo wybrane połówki są idealnie skorelowane, wówczas 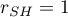 .
.
Inny wzór na współczynnik rzetelności połówkowej zaproponował Guttman (1945)4):
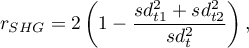
gdzie:
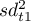 ,
, 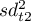 - wariancja pierwszej i drugiej połowy skali,
- wariancja pierwszej i drugiej połowy skali,
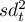 - wariancja sumy wszystkich pozycji.
- wariancja sumy wszystkich pozycji.
Uwaga!
Przyjmuje się, że aby można było uznać skalę za rzetelną, współczynniki rzetelności skali (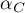 ,
, 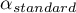 ,
, 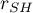 ,
, 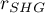 ) powinny być większe niż 0.6 i mniejsze niż 1.
) powinny być większe niż 0.6 i mniejsze niż 1.
Błąd standardowy pomiaru (ang. standard error of measurement) wyznacza się dla skali rzetelnej zgodnie z wzorem:
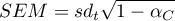 - dla współczynnika rzetelności Cronbacha
- dla współczynnika rzetelności Cronbacha
lub
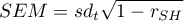 - dla współczynnika rzetelności połówkowej
- dla współczynnika rzetelności połówkowej
Okno z ustawieniami opcji rzetelności skali wywołujemy poprzez menu Statystyka→Rzetelność skali.
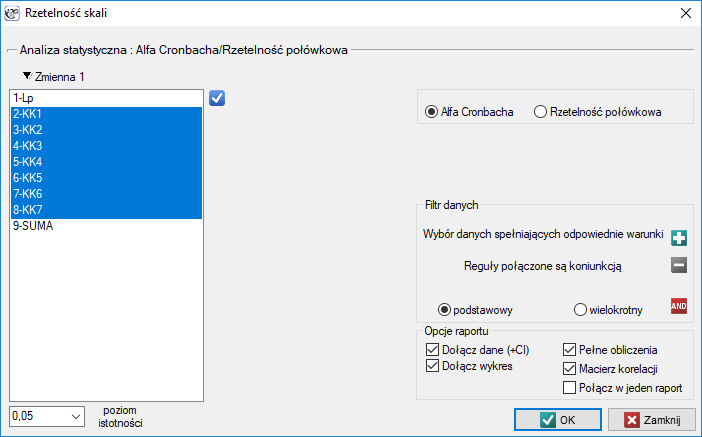
Pomocą w ocenie przydatności przyszłych pracowników pewnej firmy konsultingowej służy między innymi opracowana w firmie „skala kompetencji”. Oprócz rozmowy kwalifikacyjnej kandydaci wypełniają kwestionariusz zawierający między innymi pytania tworzące „skalę kompetencji”. Skala zawiera 7 pytań. Za każde z pytań można zyskać od 1 do 5 punktów, gzie 1 oznacza najniższą a 5 najwyższą możliwą notę. Łącznie uzyskać można 35 punktów. Punkty w tej skali uzyskane przez 24 kandydatów zawiera poniższa tabela:
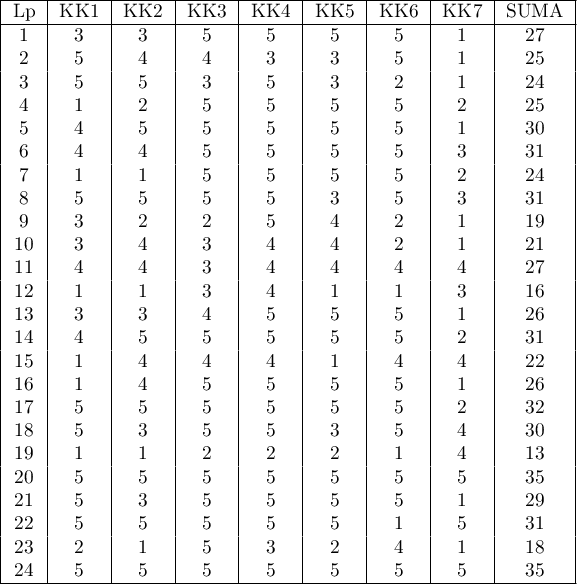
Chcemy sprawdzić dokładność zastosowanego narzędzia oceny kompetencji (zastosowanej skali). W tym celu przeprowadzona zostanie analiza rzetelności.
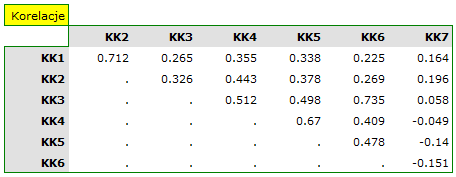
Macierz korelacji wskazuje, że ostatnia pozycja jest najsłabiej skorelowana z pozostałymi. Podejrzewamy zatem, że pozycja ta nie mierzy tego samego konstruktu, co pozostałe pozycje.
Skala kompetencji okazała się być skalą rzetelną. Współczynnik Alfa Cronbacha wynosi 0.736805, a średni współczynnik korelacji pomiędzy pozycjami skali 0.31847.
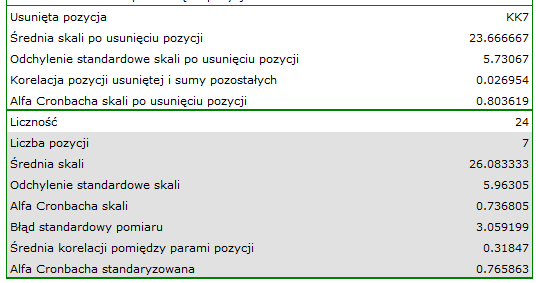
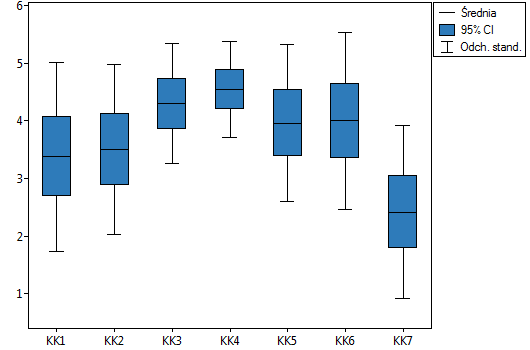
Dokładniejsza analiza każdej pozycji wskazuje, że wszystkie one, za wyjątkiem ostatniej pozycji, w podobnym stopniu wpływają na rzetelność całej skali. Korelacja pozycji KK7 z pozostałymi pozycjami skali jest najsłabsza i wynosi 0.026954. Po usunięciu ze skali pozycji KK7 wartość współczynnika Cronbacha wzrosłaby do 0.803619.
Podobne wnioski możemy wysunąć na podstawie analizy rzetelności połówkowej wykonanej na pozycjach losowo podzielonych na 2 części (KK1, KK3, KK5) (KK2, KK4, KK6, KK7).
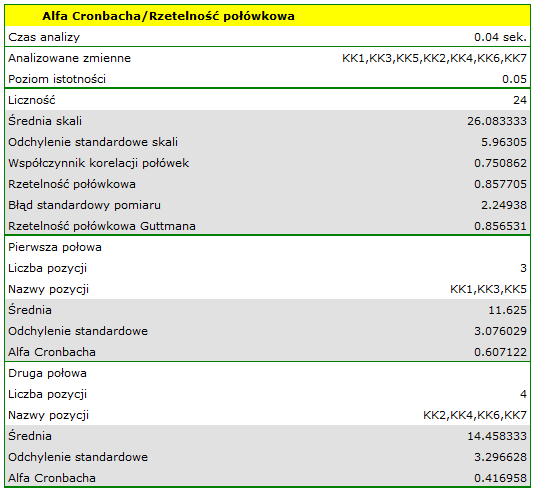
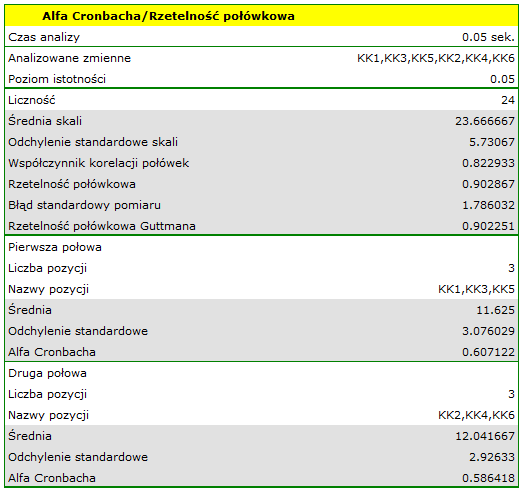
Współczynnik rzetelności połówkowej Spearmana-Browna wynosi 0.857705, a Guttmana 0.856531. Połówki są dość dobrze skorelowane - współczynnik korelacji połówek wynosi 0.750862. Jednak wartość współczynnika Alfa Cronbacha jest zbyt niska dla drugiej połówki (0.416958). Połówka ta zawiera pozycje KK7, która wykazuje słabą korelację z pozostałymi pozycjami skali. Po usunięciu tej pozycji i ponownym wykonaniu analizy, wszystkie współczynniki rzetelności rzeczywiście są wyższe.
2014/08/22 20:00
1)
Cronbach L.J. (1951), Coefficient alpha and the internal structure of tests. Psychometrika, 16(3),
297-334
2)
Spearman C. (1910), Correlation calculated from faulty data. British Journal of Psychology, 3, 271-295
3)
Brown W. (1910), Some experimental results in the correlation of mental abilities. British Journal of Psychology, 3, 296-322
4)
Guttman L. (1945), A basic for analyzing test-retest reliabilit. Psychometrika, 10, 255-282
pl/statpqpl/rzetelnpl.txt · ostatnio zmienione: 2019/12/17 17:31 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


