Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Baza Wiedzy » statpqpl » Porównanie - 2 grupy » Testy parametryczne
Pasek boczny
pl:statpqpl:porown2grpl:parpl
Spis treści
Testy parametryczne
Test Fishera-Snedecora
Test Fishera-Snedecora (ang. F-Snedecor test) opiera się na zmiennej 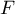 sformułowanej przez Fishera (1924), a jej rozkład opisał Snedecor. Test ten służy do weryfikacji hipotezy o równości wariancji badanej zmiennej w dwóch populacjach.
sformułowanej przez Fishera (1924), a jej rozkład opisał Snedecor. Test ten służy do weryfikacji hipotezy o równości wariancji badanej zmiennej w dwóch populacjach.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu badanej zmiennej w obu populacjach,
Hipotezy:
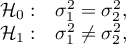
gdzie:
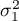 ,
, 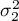
 wariancje badanej zmiennej w pierwszej i drugiej populacji.
wariancje badanej zmiennej w pierwszej i drugiej populacji.
Statystyka testowa ma postać:
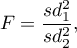
gdzie:
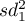 ,
, 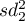
 wariancje badanej zmiennej w próbach wybranych losowo z pierwszej i drugiej populacji.
wariancje badanej zmiennej w próbach wybranych losowo z pierwszej i drugiej populacji.
Statystyka ta podlega rozkładowi F Snedecora z  i
i 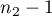 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności poziomem istotności
porównujemy z poziomem istotności poziomem istotności  :
:

Okno z ustawieniami opcji testu F Fishera-Snedecora wywołujemy poprzez menu Statystyka→Testy parametryczne→F Fisher Snedecor.
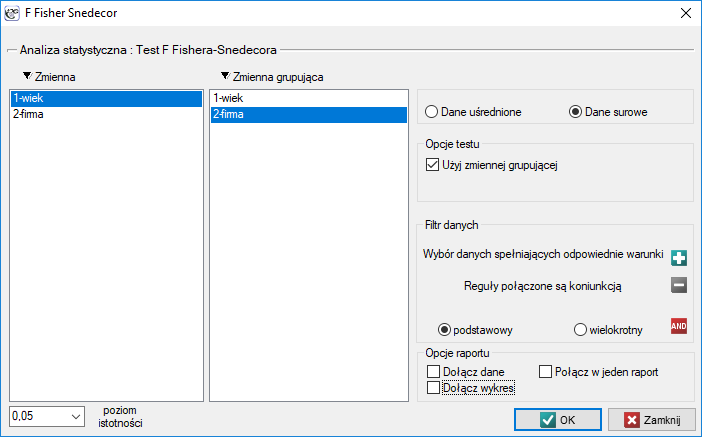
Uwaga!
Obliczenia mogą bazować na danych w postaci surowych rekordów lub danych uśrednionych tzn. odchyleniach standardowych i liczności prób.
2014/08/22 20:00
Test t-Studenta dla grup niezależnych
Test  -Studenta dla grup niezależnych (ang. t test for independent groups) służy do weryfikacji hipotezy o równości średnich badanej zmiennej w dwóch populacjach.
-Studenta dla grup niezależnych (ang. t test for independent groups) służy do weryfikacji hipotezy o równości średnich badanej zmiennej w dwóch populacjach.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu badanej zmiennej w obu populacjach,
- równość wariancji badanej zmiennej obu populacji.
Hipotezy:
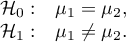
gdzie:
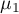 ,
, 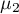
 średnie badanej zmiennej w pierwszej i drugiej populacji.
średnie badanej zmiennej w pierwszej i drugiej populacji.
Statystyka testowa ma postać:
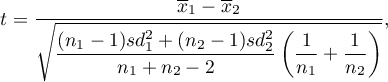
gdzie:
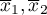
 średnie w pierwszej i drugiej próbie,
średnie w pierwszej i drugiej próbie,
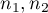
 liczności w pierwszej i drugiej próbie,
liczności w pierwszej i drugiej próbie,
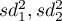
 wariancje w pierwszej i drugiej próbie.
wariancje w pierwszej i drugiej próbie.
Statystyka testowa ma rozkład t-Studenta z 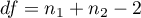 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
- wspólne odchylenie standardowe wyraża się wzorem:
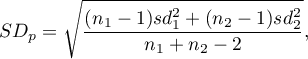
- błąd standardowy różnicy średnich wyraża się wzorem:
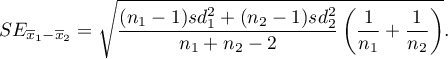
Standaryzowana wielkość efektu
Współczynnik d-Cohena określa jak dużą częścią występującej zmienności jest różnica między średnimi.
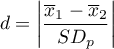
Przy interpretacji efektu badacze często posługują się ogólnymi, określonymi przez Cohena 1) wskazówkami definiującymi małą (0.2), średnią (0.5) i dużą (0.8) wielkość efektu.
Okno z ustawieniami opcji testu t-Studenta dla grup niezależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→t-Student dla grup niezależnych lub poprzez ''Kreator''.
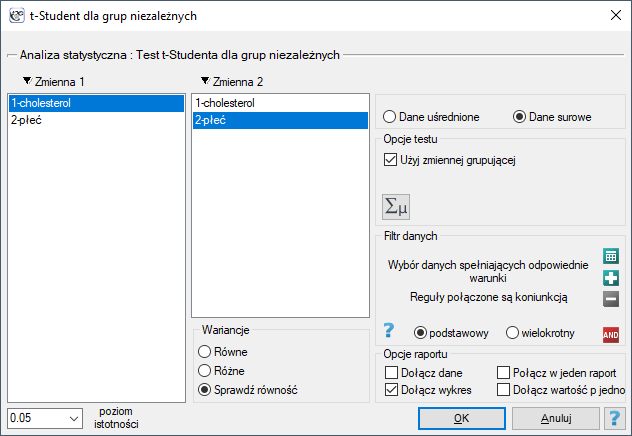
Gdy w oknie testu w opcji dotyczącej wariancji wybierzemy:
równe, wówczas zostanie wyliczony test -Studenta dla grup niezależnych,
-Studenta dla grup niezależnych,sprawdź równość, wówczas zostanie wyliczony test Fishera-Snedecora a na podstawie jego wyniku i ustawionego poziomu istotności zostanie wybrany i wyliczony test t-Studenta dla grup niezależnych z bądź bez poprawki Cochrana-Coxa.
Uwaga!
Obliczenia mogą bazować na danych w postaci surowych rekordów lub danych uśrednionych tzn. średnich arytmetycznych, odchyleniach standardowych i liczności prób.
Przykład (plik choloesterol.pqs)
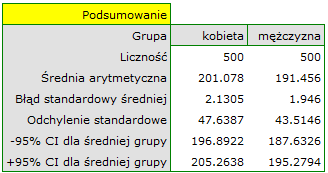
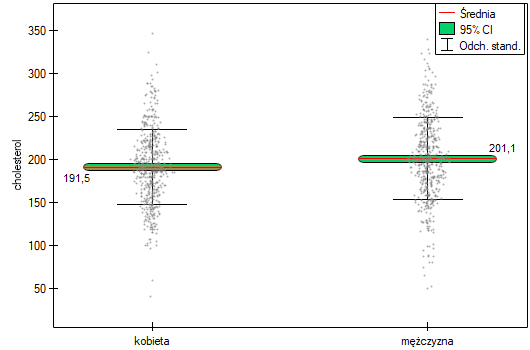
Z populacji kobiet i z populacji mężczyzn w wieku powyżej 40 roku życia wylosowano po 500 osób. Badanie dotyczyło oceny ryzyka chorób sercowo-naczyniowych. Wśród badanych parametrów znajduje się wartość cholesterolu całkowitego. Celem tego badania będzie porównanie mężczyzn i kobiet co do tej wartości. Chcemy bowiem wykazać, że te populacje różnią się już na poziomie cholesterolu całkowitego a nie tylko w obrębie cholesterolu rozbitego na frakcje.
Rozkład poziomu cholesterolu całkowitego w obu populacjach jest rozkładem normalnym (zostało to sprawdzone testem Lillieforsa). Średnia wartość cholesterolu w grupie mężczyzn wyniosła 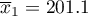 a odchylenie standardowe
a odchylenie standardowe  , w grupie kobiet odpowiednio
, w grupie kobiet odpowiednio 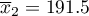 i
i  . Test Fishera-Snedecora wskazuje na niewielkie lecz istotne statystycznie (
. Test Fishera-Snedecora wskazuje na niewielkie lecz istotne statystycznie (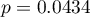 ) różnice w wariancjach. W analizie zastosowany zostanie test t-Studenta z poprawką Cochrana-Coxa.
) różnice w wariancjach. W analizie zastosowany zostanie test t-Studenta z poprawką Cochrana-Coxa.
Hipotezy:

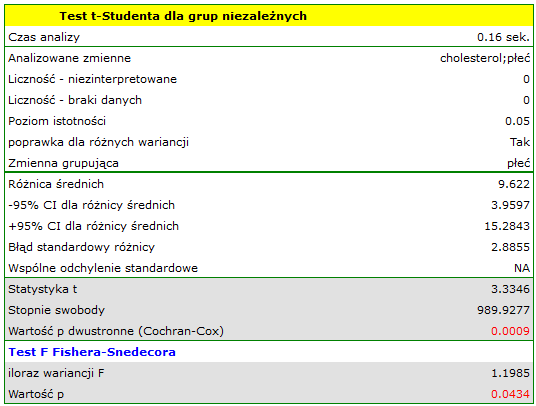
Porównując wartość 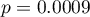 z poziomem istotności
z poziomem istotności  stwierdzamy, że kobiety i mężczyźni w Polsce różnią się istotnie statystycznie wartością cholesterolu całkowitego. Przeciętny Polak, który ukończył 40 rok życia ma wyższy cholesterol całkowity od przeciętnej Polki prawie o 10 jednostek.
stwierdzamy, że kobiety i mężczyźni w Polsce różnią się istotnie statystycznie wartością cholesterolu całkowitego. Przeciętny Polak, który ukończył 40 rok życia ma wyższy cholesterol całkowity od przeciętnej Polki prawie o 10 jednostek.
2014/08/22 20:00
Test t-Studenta z korektą Cochrana-Coxa
Poprawka Cochrana-Coxa dotyczy testu t-Studenta dla grup niezależnych (ang. Cochran-Cox adjustment), (1957)2) i jest wyliczana wówczas, gdy wariancje badanych zmiennych w obu populacjach są różne.
Statystyka testowa ma postać:
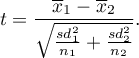
Statystyka testowa ma rozkład t-Studenta z liczbą stopni swobody zaproponowaną przez Satterthwaite (1946)3) i wyliczaną z wzoru:
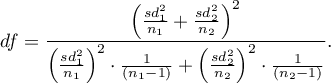
Okno z ustawieniami opcji testu t-Studenta dla grup niezależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→t-Student dla grup niezależnych lub poprzez ''Kreator''.

Gdy w oknie testu w opcji dotyczącej wariancji wybierzemy:
równe, wówczas zostanie wyliczony test -Studenta dla grup niezależnych,
-Studenta dla grup niezależnych,różne, wówczas zostanie wyliczony test -Studenta z korektą Cochrana-Coxa,
-Studenta z korektą Cochrana-Coxa,sprawdź równość, wówczas zostanie wyliczony test Fishera-Snedecora a na podstawie jego wyniku i ustawionego poziomu istotności zostanie wybrany i wyliczony test -Studenta dla grup niezależnych z bądź bez poprawki Cochrana-Coxa.
-Studenta dla grup niezależnych z bądź bez poprawki Cochrana-Coxa.
Uwaga!
Obliczenia mogą bazować na danych w postaci surowych rekordów lub danych uśrednionych tzn. średnich arytmetycznych, odchyleniach standardowych i liczności prób.
2014/08/22 20:00
Test t-Studenta dla grup zależnych
Test t-Studenta dla grup zależnych (ang. t test for dependent groups) stosuje się w sytuacji gdy pomiarów badanej zmiennej dokonujemy dwukrotnie w różnych warunkach (przy czym zakładamy, że wariancje zmiennej w obu pomiarach są sobie bliskie). Interesuje nas różnica pomiędzy parami pomiarów (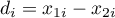 ). Różnica ta wykorzystywana jest do weryfikacji hipotezy o tym, że średnia dla niej (dla różnicy) w badanej populacji wynosi 0.
). Różnica ta wykorzystywana jest do weryfikacji hipotezy o tym, że średnia dla niej (dla różnicy) w badanej populacji wynosi 0.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu różnicy pomiarów
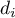 ,
,
Hipotezy:
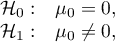
gdzie:
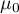 ,
,  średnia różnic
średnia różnic 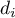 w populacji.
w populacji.
Statystyka testowa ma postać:
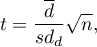
gdzie:
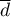
 średnia różnic
średnia różnic 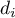 w próbie,
w próbie,
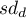
 odchylenie standardowe różnic
odchylenie standardowe różnic 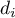 w próbie,
w próbie,

 liczność różnic
liczność różnic 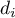 w próbie.
w próbie.
Statystyka testowa ma rozkład t-Studenta z  stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
- odchylenie standardowe różnicy wyraża się wzorem:
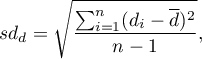
- błąd standardowy średniej różnic wyraża się wzorem:
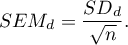
Standaryzowana wielkość efektu.
Współczynnik d-Cohena określa jak dużą częścią występującej zmienności jest różnica między średnimi, biorąc pod uwagę skorelowanie zmiennych.
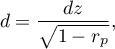 .
.
Przy interpretacji efektu badacze często posługują się ogólnymi, określonymi przez Cohena 4) wskazówkami definiującymi małą (0.2), średnią (0.5) i dużą (0.8) wielkość efektu.
Okno z ustawieniami opcji testu t-Studenta dla grup zależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→t-Student dla grup zależnych lub poprzez ''Kreator''.
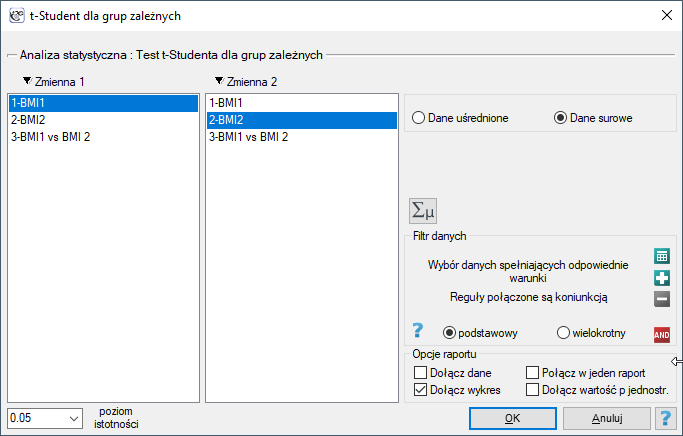
Uwaga!
Obliczenia mogą bazować na danych w postaci surowych rekordów lub danych uśrednionych tzn. średniej różnic, odchyleniu standardowym różnic i liczności próby.
W klinice leczącej zaburzenia odżywiana badano wpływ zalecanej „diety A” na zmianę masy ciała. Próbę 120 otyłych chorych poddano diecie. Zbadano dla nich poziom BMI dwukrotnie: przed wprowadzeniem diety i po 180 dniach stosowania diety. By sprawdzić skuteczność diety porównano uzyskane wyniki pomiarów BMI.
Hipotezy:
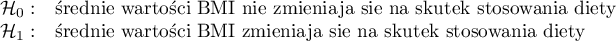

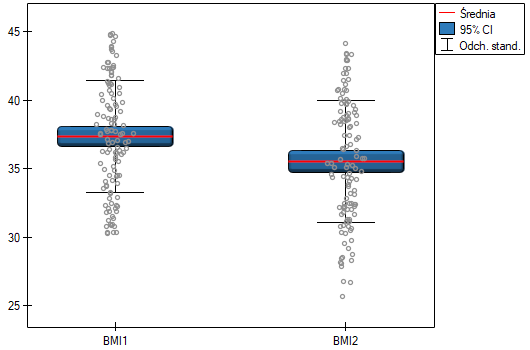
Porównując wartość 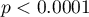 z poziomem istotności
z poziomem istotności  stwierdzamy, że średni poziom BMI zmienił się istotnie. Przed stosowaniem diety był wyższy średnio o niecałe 2 jednostki.
stwierdzamy, że średni poziom BMI zmienił się istotnie. Przed stosowaniem diety był wyższy średnio o niecałe 2 jednostki.
W badaniu możliwe było stosowanie testu t-Studenta dla grup zależnych, ponieważ rozkład różnicy pomiędzy parami pomiarów był rozkładem normalnym (test Lillieforsa, wartość 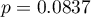 ).
).
2014/08/22 20:00
1)
, 4)
Cohen J. (1988), Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates, Hillsdale, New Jersey
2)
Cochran W.G. and Cox G.M. (1957), Experimental designs (2nd 4.). New York: John Wiley and Sons.
3)
Satterthwaite F.E. (1946), An approximate distribution of estimates of variance components. Biometrics Bulletin, 2, 1 10-1 14
pl/statpqpl/porown2grpl/parpl.txt · ostatnio zmienione: 2014/08/22 21:17 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


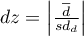 ,
,
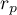 –
– 