Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Baza Wiedzy » statpqpl » Porównanie - 1 grupa » Testy parametryczne
Pasek boczny
pl:statpqpl:porown1grpl:parpl
Testy parametryczne
Test t-Studenta dla pojedynczej próby
Test t-Studenta dla pojedynczej próby (ang. single-sample t test) służy do weryfikacji hipotezy, że badana próba o średniej 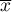 pochodzi z populacji dla której średnia
pochodzi z populacji dla której średnia 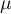 to zadana wartość.
to zadana wartość.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu badanej cechy.
Hipotezy:
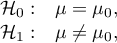
gdzie:
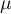 - średnia cechy w populacji reprezentowanej przez próbę,
- średnia cechy w populacji reprezentowanej przez próbę,
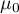 - zadana wartość.
- zadana wartość.
Statystyka testowa ma postać:
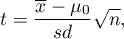
gdzie:
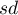 - odchylenie standardowe z próby,
- odchylenie standardowe z próby,
 - liczność próby.
- liczność próby.
Statystyka testowa ma rozkład t-Studenta z  stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:
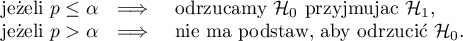
Uwaga!
Gdy próba jest duża i znane jest odchylenie standardowe z populacji wówczas statystykę testową można wyznaczyć z wzoru:
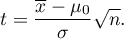 Tak wyznaczona statystyka testowa ma rozkład normalny. Przy
Tak wyznaczona statystyka testowa ma rozkład normalny. Przy 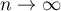 rozkład
rozkład  -Studenta jest zbieżny do rozkładu normalnego
-Studenta jest zbieżny do rozkładu normalnego 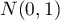 . W praktyce przyjmuje się, że dla
. W praktyce przyjmuje się, że dla  rozkład
rozkład  -Studenta można aproksymować rozkładem normalnym.
-Studenta można aproksymować rozkładem normalnym.
Standaryzowana wielkość efektu
Współczynnik d-Cohena określa jak dużą częścią występującej zmienności jest różnica między średnimi.
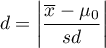
Przy interpretacji efektu badacze często posługują się ogólnymi, określonymi przez Cohena 1) wskazówkami definiującymi małą (0.2), średnią (0.5) i dużą (0.8) wielkość efektu.
Okno z ustawieniami opcji testu t-Studenta dla pojedynczej próby wywołujemy poprzez menu Statystyka→Testy parametryczne→t-Student lub poprzez ''Kreator''.
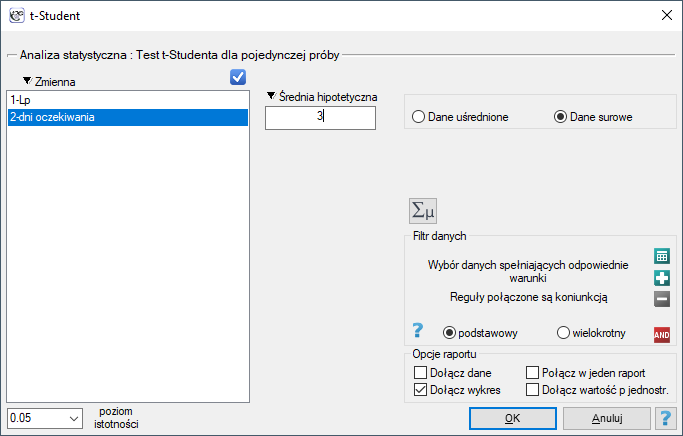
Uwaga!
Obliczenia mogą bazować na danych w postaci surowych rekordów lub danych uśrednionych tzn. średniej arytmetycznej, odchyleniu standardowym i liczności próby.
Przykład (plik kurier.pqs)
Chcemy sprawdzić, czy czas oczekiwania na dostarczenie przesyłki przez pewna firmę kurierską to przeciętnie 3 dni 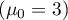 . W tym celu z populacji klientów tej firmy wylosowano próbę liczącą 22 osoby i zapisano informacje o liczbie dni, jakie minęły od dnia nadania przesyłki do jej dostarczenia, były to następujące wielkości: (1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7).}
. W tym celu z populacji klientów tej firmy wylosowano próbę liczącą 22 osoby i zapisano informacje o liczbie dni, jakie minęły od dnia nadania przesyłki do jej dostarczenia, były to następujące wielkości: (1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7).}
Liczba dni oczekiwania na przesyłkę w badanej populacji spełnia założenie normalności rozkładu.
Hipotezy:


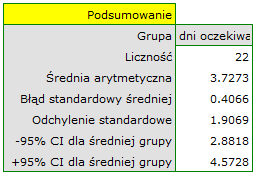
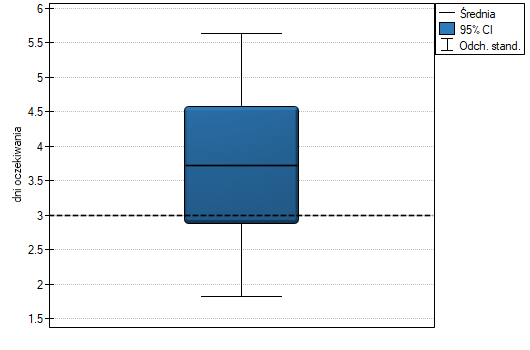
Porównując wartość 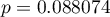 testu
testu  -Studenta z poziomem istotności
-Studenta z poziomem istotności  stwierdzamy, że nie ma podstaw by odrzucić hipotezę zerową mówiącą, że średnia liczba dni oczekiwania na dostarczenie przesyłki przez analizowaną firmę kurierską wynosi 3. Dla badanej próby średnia to
stwierdzamy, że nie ma podstaw by odrzucić hipotezę zerową mówiącą, że średnia liczba dni oczekiwania na dostarczenie przesyłki przez analizowaną firmę kurierską wynosi 3. Dla badanej próby średnia to 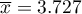 a odchylenie standardowe
a odchylenie standardowe 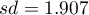 .
.
2014/08/22 20:00
1)
Cohen J. (1988), Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates, Hillsdale, New Jersey
pl/statpqpl/porown1grpl/parpl.txt · ostatnio zmienione: 2014/08/22 21:16 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


