The Chi-square test for multidimensional contingency tables

Basic assumptions:

Hypotheses:

$\begin{array}{cl} \mathcal{H}_0: & O_{ij...}=E_{ij...} $ for all categories,$\\ \mathcal{H}_1: & O_{ij...} \neq E_{ij...} $ for at least one category,$ \end{array}$

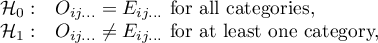
where:

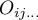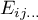
$O_{ij...}$ and $E_{ij...}$ $-$ observed frequencies in a contingency table and the corresponding expected frequencies.

The test statistic is defined by:

\begin{displaymath} \chi^2=\sum_{i=1}^r\sum_{j=1}^c\sum...\sum\frac{(O_{ij...}-E_{ij...})^2}{E_{ij...}}. \end{displaymath}

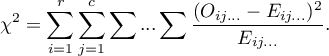
This statistic asymptotically (for large expected frequencies) has the Chi-square distribution with a number of degrees of freedom calculated using the formula: 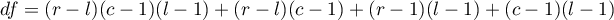$df = (r - l)(c - 1)(l - 1) + (r- l)(c- 1) + (r- 1)(l- 1) + (c- 1)(l- 1)$ - for 3-dimensional tables.

The p-value, designated on the basis of the test statistic, is compared with the significance level $\alpha$:

\begin{array}{ccl} $ if $ p \le \alpha & \Longrightarrow & $ reject $ \mathcal{H}_0 $ and accept $ \mathcal{H}_1, \\ $ if $ p > \alpha & \Longrightarrow & $ there is no reason to reject $ \mathcal{H}_0. \\ \end{array}

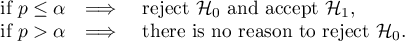
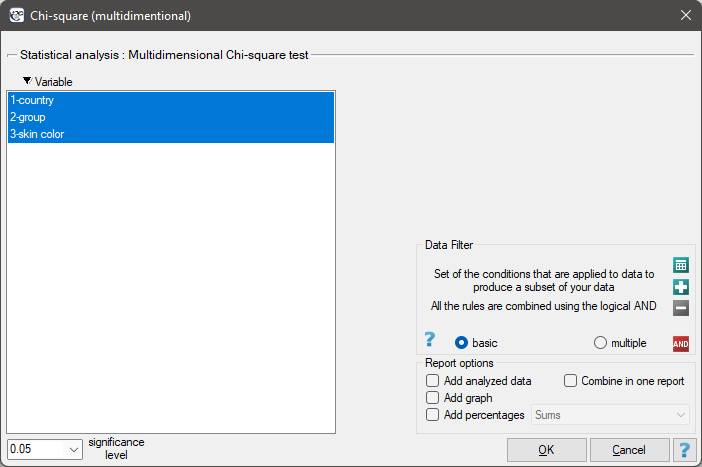
The settings window with the Chi-square (multidimensional) test can be opened in Statistics menu → NonParametric tests (unordered categories)→Chi-square (multidimensional) or in ''Wizard''.

Note

This test can be calculated only on the basis of raw data.

1)
Cochran W.G. (1952), The chi-square goodness-of-fit test. Annals of Mathematical Statistics, 23, 315-345