Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:redpl:pcapl:zasadnpl
Zasadność stosowania Analizy składowych głównych
Jeśli zmienne nie są skorelowane (współczynnik korelacji Pearsona jest bliski 0), to wówczas przeprowadzanie analizy składowych głównych nie ma sensu. W takiej sytuacji bowiem każda zmienna stanowi już odrębną składową.
Test Bartletta
Test ten wykorzystywany jest do weryfikacji hipotezy o tym, że współczynniki korelacji pomiędzy zmiennymi są zerowe (czyli macierz korelacji jest macierzą jednostkową).
Hipotezy:
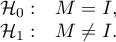
gdzie:
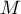 – macierz wariancji lub kowariancji zmiennych pierwotnych
– macierz wariancji lub kowariancji zmiennych pierwotnych 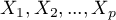 ,
,
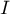 – macierz jednostkowa (1 na głównej przekątnej, 0 poza nią).
– macierz jednostkowa (1 na głównej przekątnej, 0 poza nią).
Statystyka testowa ma postać:
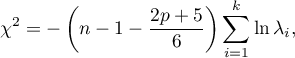
gdzie:
 – liczba zmiennych pierwotnych,
– liczba zmiennych pierwotnych,
 – liczność (liczba przypadków),
– liczność (liczba przypadków),
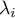 –
–  -ta wartość własna.
-ta wartość własna.
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z 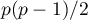 stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Współczynnik Kaisera-Mayera-Olkina
Współczynnik ten wykorzystywany jest do sprawdzania stopnia skorelowania zmiennych pierwotnych, czyli siły dowodów świadczących na rzecz sensowności przeprowadzania analizy składowych głównych.
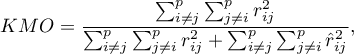
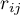 – współczynnik korelacji pomiędzy
– współczynnik korelacji pomiędzy  -tą a
-tą a  -tą zmienną,
-tą zmienną,
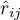 – współczynnik korelacji cząstkowej pomiędzy
– współczynnik korelacji cząstkowej pomiędzy  -tą a
-tą a  -tą zmienną.
-tą zmienną.
Wartość współczynnika Kaisera należy do przedziału 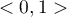 , gdzie wartości niskie świadczą o braku podstaw do przeprowadzania analizy składowych głównych, a wartości wysokie są przesłanką do przeprowadzania tej analizy.
, gdzie wartości niskie świadczą o braku podstaw do przeprowadzania analizy składowych głównych, a wartości wysokie są przesłanką do przeprowadzania tej analizy.
Ten klasyczny zestaw danych pierwotnie ukazał się w pracy R.A. Fishera 19361), gdzie przedstawiona została analiza dyskryminacyjna. Plik zawiera pomiary (w centymetrach) długości i szerokości płatków i działek kielicha dla 3 odmian kwiatu irysa. Poddane badaniu gatunki to setosa, versicolor i virginica. Interesujące jest określenie sposobu rozróżniania tych gatunków na bazie uzyskanych pomiarów.

Rycina pochodzi z pracy Lee i innych (2006r): „Application of a noisy data classification technique to determine the occurrence of flashover in compartment fires”
Analiza składowych głównych pozwoli na wskazanie tych pomiarów (długości i szerokości płatków i działek kielicha), które dają badaczowi najwięcej informacji o obserwowanych kwiatach.
Pierwszym etapem wykonywanym jeszcze przed przystąpieniem do wyznaczania i analizowania składowych, jest sprawdzenie celowości przeprowadzenia tej analizy. Zaczynamy więc od wyznaczenia macierzy korelacji zmiennych oraz przeanalizowania uzyskanych korelacji przy wykorzystaniu testu Bartletta i współczynnika KMO.
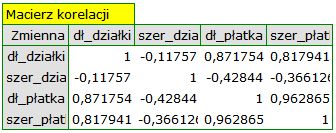
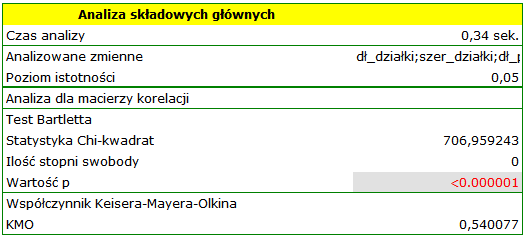
Wartość  statystyki Bartletta wskazuje na prawdziwość hipotezy mówiącej o istotnej różnicy pomiędzy uzyskaną macierzą korelacji a macierzą jednostkową, czyli znacznym skorelowaniu zmiennych. Uzyskany współczynnik KMO jest natomiast przeciętny i wynosi 0.54. Wskazania do przeprowadzenia analizy składowych głównych uznajemy za wystarczające.
statystyki Bartletta wskazuje na prawdziwość hipotezy mówiącej o istotnej różnicy pomiędzy uzyskaną macierzą korelacji a macierzą jednostkową, czyli znacznym skorelowaniu zmiennych. Uzyskany współczynnik KMO jest natomiast przeciętny i wynosi 0.54. Wskazania do przeprowadzenia analizy składowych głównych uznajemy za wystarczające.
Pierwszym wynikiem tej analizy, na który należy zwrócić szczególną uwagę są wartości własne:
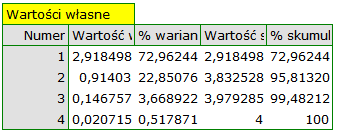
Uzyskane wartości własne wskazują, że dwie lub nawet jedna składowa główna w dobry sposób opiszą nasze dane. Wartość własna dla pierwszej składowej wynosi 2.92 a procent wyjaśnionej przez nią wariancji to 72.96. Druga składowa wyjaśnia już znacznie mniej wariancji, bo 22.85% a jej wartość własna to 0.91. Według kryterium Kaisera wystarczająca w interpretacji jest tylko jedna składowa główna, gdyż tylko dla pierwszej składowej wartość własna jest większa niż 1. Patrząc jednak na wykres osypiska można wysnuć wniosek, że linia spadkowa przechodzi w poziomą dopiero od 3 składowej głównej.
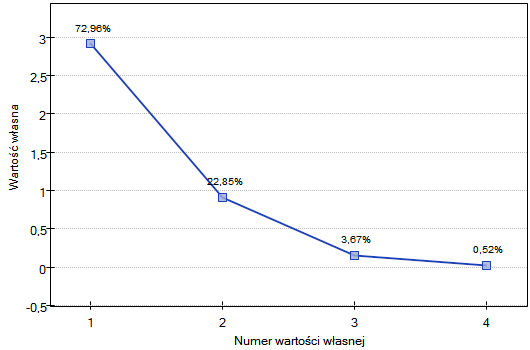
Zgodnie z tym wskazaniem dwie pierwsze składowe wnoszą istotną informację. Łącznie dwie pierwsze składowe wyjaśniają sporo bo aż 95.81% wariancji (patrz kolumna % skumulowany).
Zasoby zmienności wspólnej dla pierwszej składowej są wysokie dla wszystkich zmiennych pierwotnych za wyjątkiem zmiennej szerokość działki, dla której wynoszą 21,17%. Oznacza to, że gdybyśmy pozostali przy interpretacji tylko pierwszej składowej, to zmienna szerokość działki zostałaby odzwierciedlona w niewielkiej części.
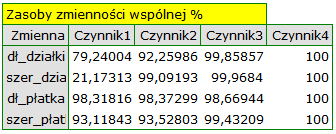
Dla dwóch pierwszych składowych zasoby zmienności wspólnej są już na podobnym, bardzo wysokim poziomie i dla każdej z analizowanych zmiennych przekraczają 90%, czyli wariancja każdej zmiennej jest reprezentowana przy użyciu tych składowych w ponad 90%.
Zebrawszy całą tą wiedzę zdecydowano się na wyodrębnienie i interpretację 2 składowych.
By przyjrzeć się dokładniej powiązaniu składowych głównych i zmiennych pierwotnych czyli długości i szerokości płatków i działek kielicha interpretujemy: wektory własne, ładunki czynnikowe oraz wkłady zmiennych.
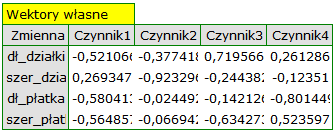
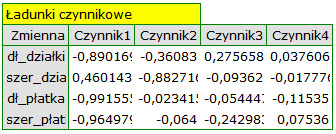
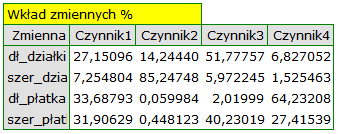
Poszczególne zmienne pierwotne w różny sposób oddziałują na pierwszą składową główną. Ułóżmy je kolejno według wielkości tego wpływu:
- Długość płatka jest ujemnie skorelowana z pierwszą składową, a zatem czym dłuższy płatek, tym niższe wartości tej składowej. Wektor własny dla długości płatka jest największy w tej składowej i wynosi -0.58. Jego ładunek czynnikowy informuje, że korelacja pomiędzy pierwszą składową główną a długością płatka jest bardzo wysoka i wynosi -0.99 co daje 33.69\% wkładu w pierwszą składową;
- Szerokość płatka ma nieco tylko mniejszy wpływ na pierwszą składową i jest z nią również ujemnie skorelowana;
- Długość działki interpretujemy podobnie jak poprzednie dwie zmienne ale jej wpływ na pierwszą składową jest mniejszy;
- Szerokość działki jest najsłabiej skorelowana z pierwszą składową i znak tej korelacji jest dodatni.
Druga składowa reprezentuje głównie zmienną pierwotną: szerokość działki; pozostałe zmienne pierwotne są w niej odzwierciedlone w niewielkim stopniu. Wektor własny, ładunek czynnikowy oraz wkład zmiennej szerokość działki jest w składowej drugiej najwyższy.
Każda składowa główna wyznacza homogeniczną grupę zmiennych pierwotnych. Pierwszą składową nazwiemy „rozmiar płatka”, gdyż najbardziej znaczącymi dla niej zmiennymi są te zmienne, które niosą informacje o płatku, choć trzeba zaznaczyć, że długość działki również wpływa znacznie na wartość tej składowej. W interpretacji pamiętamy, że czym większe są wartości tej składowej , tym mniejsze są płatki.
Drugą składową nazwiemy natomiast „szerokość działki” gdyż tylko szerokość działki w większym stopniu odzwierciedlona jest w drugiej składowej. Przy czym, im większe są wartości tej składowej, tym węższa jest działka.
Ostatecznie składowe wygenerujemy wybierając w oknie analizy opcję: Dołącz składowe główne. Fragment uzyskanego wyniku przedstawiamy poniżej:
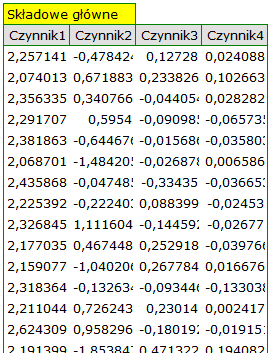
Aby dwie pierwsze składowe można było wykorzystać zamiast wcześniejszych czerech zmiennych pierwotnych, ostatecznie przeklejamy je do arkusza danych. Dalsze planowane przez siebie statystyki badacz może teraz przeprowadzić na dwóch nowych, nieskorelowanych zmiennych.
- [Analiza wykresów dwóch pierwszych składowych]
Analiza wykresów nie dość, że doprowadzi badacza do tych samych wniosków, co analiza tabel, to da możliwość wnikliwszej oceny uzyskanych wyników. - [Wykres ładunków czynnikowych]
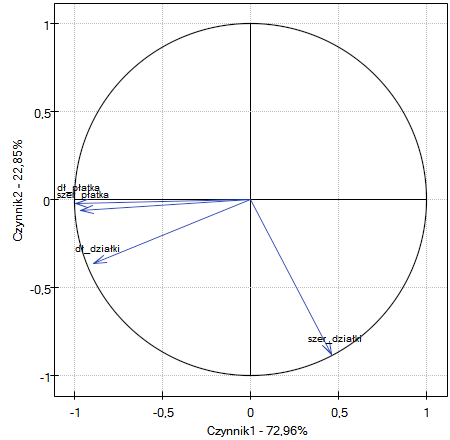
Wykres przedstawia dwie pierwsze składowe główne, które reprezentują 72.96% wariancji i 22.85% wariancji co daje łącznie 95.81% wariancji zmiennych pierwotnych
Wektory reprezentujące zmienne pierwotne nieomalże sięgają brzegów koła jednostkowego (koła o promieniu 1), a zatem wszystkie one są bardzo dobrze reprezentowane przez dwie pierwsze składowe główne tworzące układ współrzędnych.
Kąt pomiędzy wektorami obrazującymi długość płatka, szerokość płatka i długość działki jest niewielki, co oznacza duże skorelowanie tych zmiennych. Skorelowanie zaś tych zmiennych ze składowymi tworzącymi układ jest negatywne - wektory znajdują się w III ćwiartce układu. Przy czym wyższe wartości współrzędnych końca wektora obserwowane są dla składowej pierwszej niż drugiej. Takie ułożenie wektorów świadczy o tym, że tworzą one grupę jednorodną, która jest reprezentowana głównie przez składową pierwszą.
Zupełnie inny kierunek wskazuje wektor dotyczący szerokości działki, który jest w niewielkim stopniu skorelowany z pozostałymi zmiennymi pierwotnymi o czym świadczy kąt nachylenia do pozostałych zmiennych pierwotnych, który jest bliski kątowi prostemu. Skorelowanie tego wektora z pierwszą składową jest pozytywne i niezbyt wysokie (niska wartość pierwszej współrzędnej końca wektora) a z drugą składową negatywne i wysokie (wysoka wartość drugiej współrzędnej końca wektora). Wnioskujemy z tego, że szerokość działki jako jedyna zmienna pierwotna reprezentowana jest dobrze przez drugą składową.
- [Biplot]
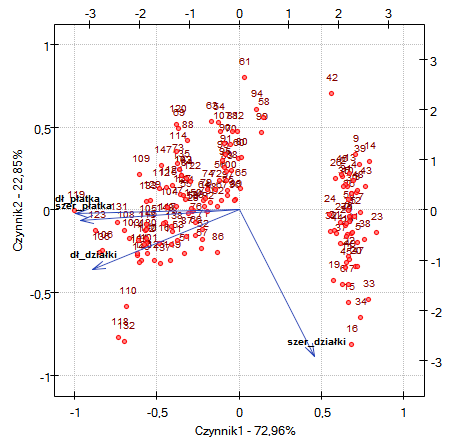
Biplot przedstawia dwie serie danych rozpięte na dwóch pierwszych składowych. Jedną serią są wektory zmiennych pierwotnych, które przedstawione były na poprzednim wykresie, a drugą serią są punkty niosące informacje o poszczególnych kwiatach. Przy czym wartości drugiej serii odczytujemy na górnej osi  i prawej osi
i prawej osi  . Sposób interpretacji wektorów, czyli pierwszej serii omówiliśmy przy poprzednim wykresie. By zrozumieć interpretację punktów skupimy się na kwiatach o numerze 33 i 34 oraz o numerze 109.
. Sposób interpretacji wektorów, czyli pierwszej serii omówiliśmy przy poprzednim wykresie. By zrozumieć interpretację punktów skupimy się na kwiatach o numerze 33 i 34 oraz o numerze 109.
Kwiaty o numerze 33 i 34 są do siebie podobne - odległość punktu 33 i 34 jest niewieka. Oba punkty mają sporo większą niż przeciętna wartość pierwszej i sporo mniejszą niż przeciętna wartość drugiej składowej. Wartość przeciętna, a zatem średnia arytmetyczna obu składowych wynosi 0, więc jest to środek układu współrzędnych. Pamiętając, że pierwsza składowa to głównie rozmiar płatków a druga to szerokość działki możemy powiedzieć, że kwiaty 33 i 34 mają niewielkie płatki i dużą szerokość działki. Natomiast kwiat 109 reprezentuje punkt znacznie oddalony od pozostałych dwóch punktów. Jest to kwiat o ujemnej pierwszej składowej i dodatniej lecz nie wysokiej drugiej składowej. Zatem jest to kwiat o stosunkowo dużych płatkach i szerokości działki nieco tylko mniejszej niż przeciętna.
Podobne informacje uzyskamy rzutując punkty na linie przedłużające wektory zmiennych pierwotnych. Przykładowo kwiat 33 wykazuje się dużą szerokością działki (wysokie i dodatnie wartości rzutowania na zmienną pierwotną szerokość działki) ale niskimi wartościami pozostałych zmiennych pierwotnych (ujemne wartości rzutowania na przedłużenie wektorów obrazujących pozostałe zmienne pierwotne).
1)
Fisher R.A. (1936), The use of multiple measurements in taxonomic problems. Annals of Eugenics 7 (2): 179–188
statpqpl/redpl/pcapl/zasadnpl.txt · ostatnio zmienione: 2022/02/28 14:11 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

