Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
pl:statpqpl:zgodnpl:nparpl:kappaflpl
Współczynnik Kappa Fleissa i test badający jego istotność
Współczynnik ten określa zgodność pomiarów prowadzonych przez kliku sędziów (Fleiss, 19711)) i jest rozszerzeniem współczynnika Kappa Cohena, pozwalającego na badanie zgodności jedynie dwóch sędziów. Przy czym, należy zaznaczyć że każdy z  losowo wybranych obiektów może być oceniany przez inny losowy zestaw
losowo wybranych obiektów może być oceniany przez inny losowy zestaw  sędziów. Analiza opiera się na danych przekształconych do tabeli o
sędziów. Analiza opiera się na danych przekształconych do tabeli o  wierszach i
wierszach i  kolumnach, gdzie
kolumnach, gdzie  stanowi liczbę możliwych kategorii, do których sędziowie przydzielają badane obiekty. Zatem w każdym wierszu tabeli podano
stanowi liczbę możliwych kategorii, do których sędziowie przydzielają badane obiekty. Zatem w każdym wierszu tabeli podano 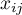 czyli liczbę sędziów wydających określone w danej kolumnie opinie.
czyli liczbę sędziów wydających określone w danej kolumnie opinie.
Współczynnik Kappa ( ) wyraża się wtedy wzorem:
) wyraża się wtedy wzorem:
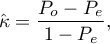
gdzie:
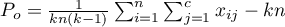 ,
,
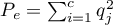 ,
,
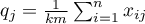 .
.
Wartość 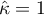 oznacza pełną zgodność sędziów, natomiast
oznacza pełną zgodność sędziów, natomiast 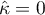 oznacza zgodność jaka powstałaby, gdyby opinie sędziów wydane były w sposób losowy. Wartości ujemne Kappa wskazują natomiast na zgodność mniejszą niż na poziomie losowym.
oznacza zgodność jaka powstałaby, gdyby opinie sędziów wydane były w sposób losowy. Wartości ujemne Kappa wskazują natomiast na zgodność mniejszą niż na poziomie losowym.
Dla współczynnika  można wyznaczyć błąd standardowy
można wyznaczyć błąd standardowy 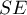 , który pozwala na zbadanie istotności statystycznej i wyznaczenie asymptotycznych przedziałów ufności.
, który pozwala na zbadanie istotności statystycznej i wyznaczenie asymptotycznych przedziałów ufności.
Test Z do sprawdzania istotności współczynnika Kappa Fleissa ( ) (ang. The Z test of significance for the Fleiss's Kappa) Fleiss (20032)) służy do weryfikacji hipotezy o zgodności ocen kilku sędziów i opiera się na współczynniku
) (ang. The Z test of significance for the Fleiss's Kappa) Fleiss (20032)) służy do weryfikacji hipotezy o zgodności ocen kilku sędziów i opiera się na współczynniku  wyliczonym dla próby.
wyliczonym dla próby.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę.
Hipotezy:
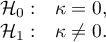
Statystyka testowa ma postać:
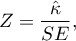
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga! Wyznaczanie współczynnika Kappa Fleissa zbliżone jest koncepcyjnie do metody Mantela-Haenszela. Wyznaczona Kappa jest ogólną miarą podsumowującą zgodność wszystkich ocen sędziowskich i może być wyznaczona jako Kappa utworzona z poszczególnych warstw, którymi są konkretne oceny sędziowskie (Fleiss, 20033)). Dlatego, jako podsumowanie każdej warstwy można wyznaczyć zgodność sędziowską (współczynnik Kappa) podsumowującą każdą możliwą ocenę z osobna.
Okno z ustawieniami opcji testu istotności Kappa-Fleissa wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Kappa-Fleissa
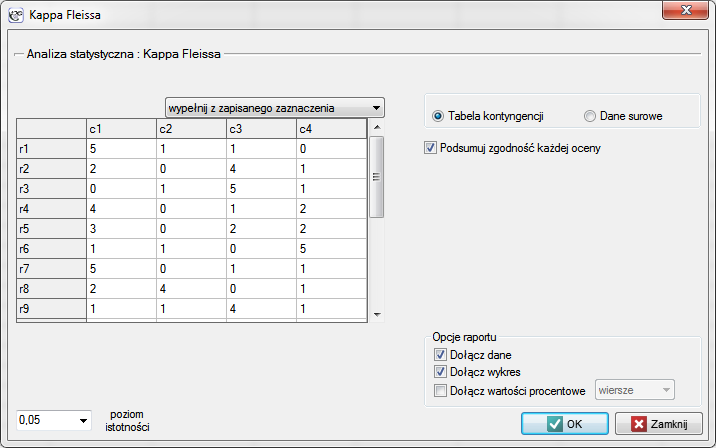
Przykład (plik temperament.pqs)
20 ochotników bierze udział w zabawie mającej na celu ustalenie typu osobowości badanych. Każdy z ochotników dysponuje oceną wystawioną przez 7 różnych obserwatorów (najczęściej osób z bliskiego otoczenia lub rodziny). Każdy z obserwatorów został zapoznany z podstawowymi cechami opisującymi temperament w poszczególnych typach osobowości: choleryk, flegmatyk, melancholik, sangwinik. Badamy zgodność obserwatorów w przypisywaniu typów osobowości. Fragment danych przedstawia poniższa tabela.
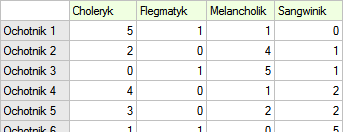
Hipotezy:
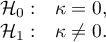

Obserwujemy nieduży współczynnik Kappa = 0.244918, lecz istotny statystycznie (p<0.000001), co oznacza nieprzypadkową zgodność ocen sędziowskich. Istotna zgodność dotyczy każdej oceny, czego potwierdzeniem jest raport podsumowujący zgodność dla każdej warstwy (dla każdej oceny) oraz wykres prezentujący poszczególne współczynniki Kappa i Kappę podsumowującą całość.
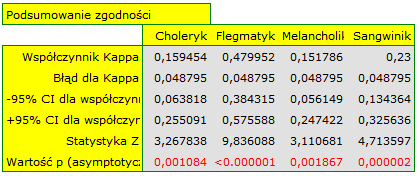
Ciekawy może być fakt, że najwyższa zgodność dotyczy oceny flegmatyków (Kappa=0.479952).
Przy niewielkiej liczbie obserwowanych osób warto również wykonać wykres obrazujący w jaki sposób obserwatorzy oceniali każdą z nich.
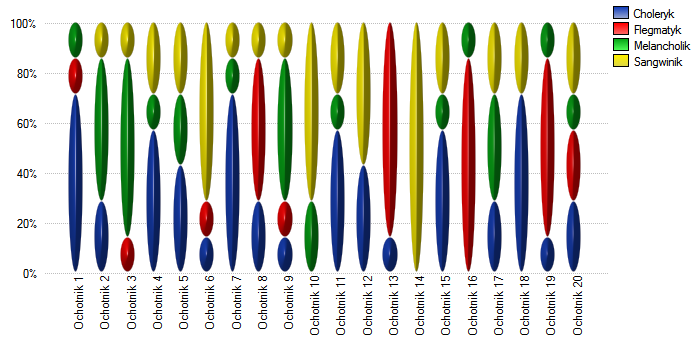
W tym przypadku tylko osoba nr 14 uzyskała jednoznaczną ocenę typu osobowości - sangwinik. Osoby nr 13 i 16 ocenione były jako typ flegmatyk przez 6 obserwatorów (na 7 możliwych). W przypadku pozostałych osób panowała nieco mniejsza zgodność ocen. Najtrudniejszy do zdefiniowania typ osobowości wydaje się cechować ostatnią osobę, która uzyskała najbardziej różnorodny zestaw ocen.
pl/statpqpl/zgodnpl/nparpl/kappaflpl.txt · ostatnio zmienione: 2022/01/23 21:27 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


