Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
pl:statpqpl:porown2grpl:nparpl:trendpl
Test chi-kwadrat dla trendu
Test  dla trendu nazywany również testem dla trendu Cochrana-Armitage (ang. Cochran-Armitage test for trend)1)2) służy do weryfikacji hipotezy o istnieniu trendu w proporcjach dla poszczególnych kategorii badanej zmiennej (cechy). Opiera się na danych zebranych w postaci tabeli kontyngencji 2 cech, z których pierwsza ma możliwe
dla trendu nazywany również testem dla trendu Cochrana-Armitage (ang. Cochran-Armitage test for trend)1)2) służy do weryfikacji hipotezy o istnieniu trendu w proporcjach dla poszczególnych kategorii badanej zmiennej (cechy). Opiera się na danych zebranych w postaci tabeli kontyngencji 2 cech, z których pierwsza ma możliwe  uporządkowanych kategorii:
uporządkowanych kategorii: 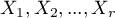 a druga 2 kategorie
a druga 2 kategorie 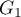 ,
, 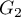 .
.
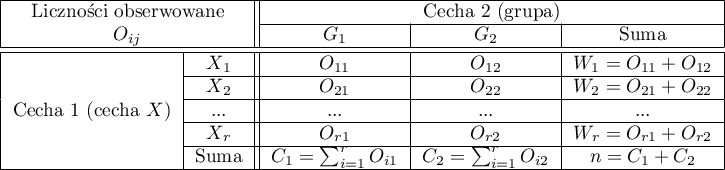
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
- model niezależny (druga cecha, to 2 niezależne grupy).
Niech 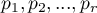 oznaczają proporcje
oznaczają proporcje 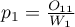 ,
, 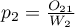 ,…,
,…, 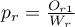 .
.
Hipotezy:
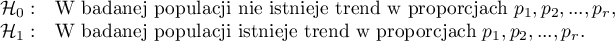
Statystyka testowa ma postać:
![LaTeX \begin{displaymath}
\chi^2=\frac{\left[\left(\sum_{i=1}^r i\cdot O_{i1}\right) -C_1\left(\sum_{i=1}^r\frac{i\cdot W_i}{n}\right)\right]^2}{\frac{C_1}{n}\left(1-\frac{C_1}{n}\right)\left[\left(\sum_{i=1}^n i^2 W_i\right)-n\left(\sum_{i=1}^n\frac{i \cdot W_i}{n}\right)^2\right]}.
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/imgd32bd126527cf05771f082e9a0735129.png)
Statystyk ta ma rozkład chi-kwadrat z 1 stopniem swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności poziomem istotności
porównujemy z poziomem istotności poziomem istotności  :
:

Okno z ustawieniami opcji testu Chi-kwadrat dla trendu wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Chi-kwadrat, Fisher, OR/RR, opcja Fisher, Yates i inne…→Chi-kwadrat dla trendu.
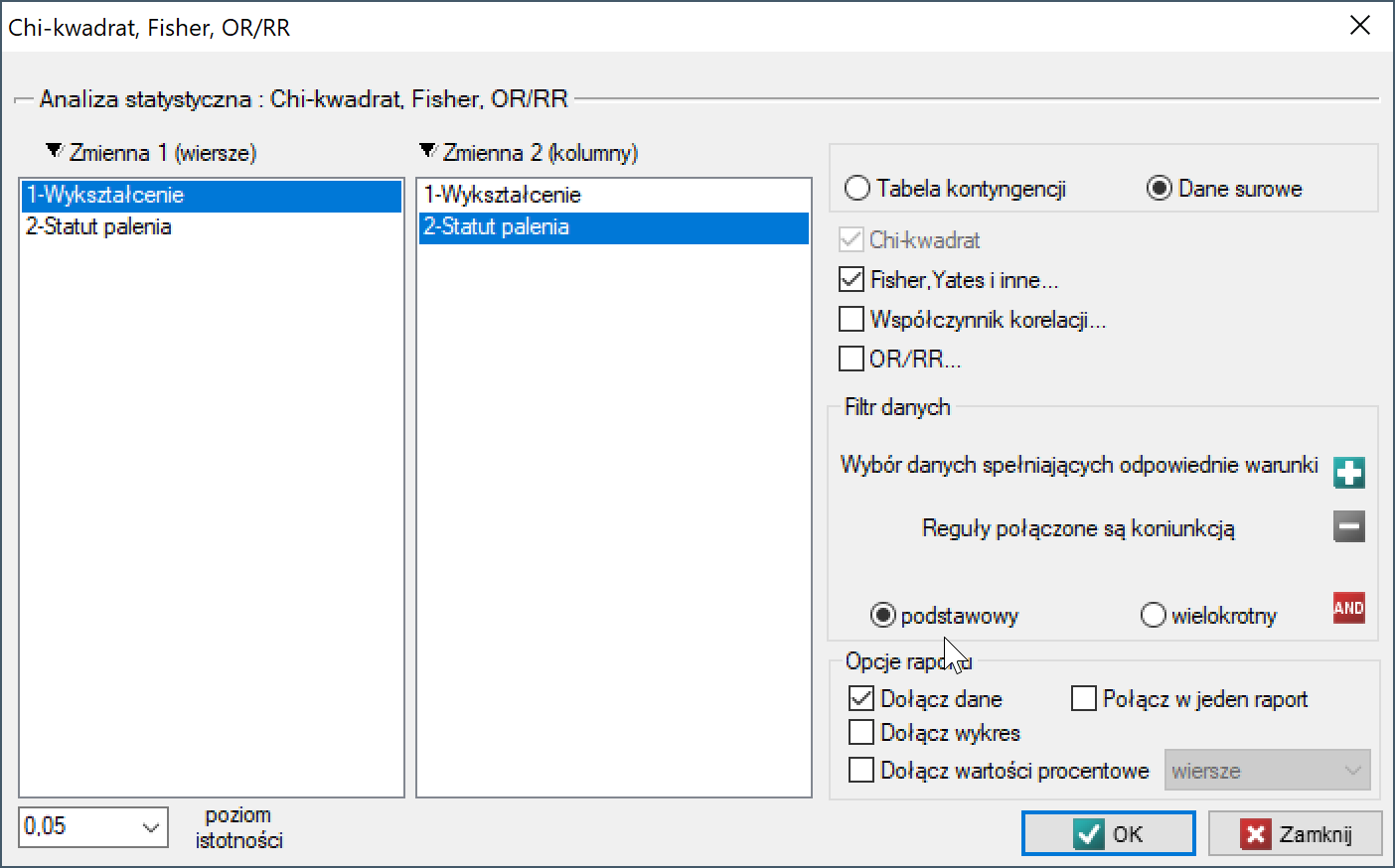
Przykład (palenie-wykształcenie.pqs)
Sprawdzamy czy palenie papierosów związane jest z wykształceniem mieszkańców pewnej wsi. Wylosowano próbę 122 osób. Dane zapisano w pliku.
Zakładamy, że zależność może być dwojakiego typu tzn. czym bardziej wykształceni ludzie, tym częściej palą lub czym bardziej wykształceni ludzie, tym rzadziej palą. Poszukujemy zatem rosnącego lub malejącego trendu.
Przed przystąpieniem do analizy musimy przygotować dane, tzn. musimy wskazać kolejność w jakiej mają się pojawiać kategorie wykształcenia. W tym celu z właściwości zmiennej Wykształcenie wybieramy Kody/Etykiety/Format… i nadajemy kolejność podając kolejne liczby naturalne. Przypisujemy również etykiety.
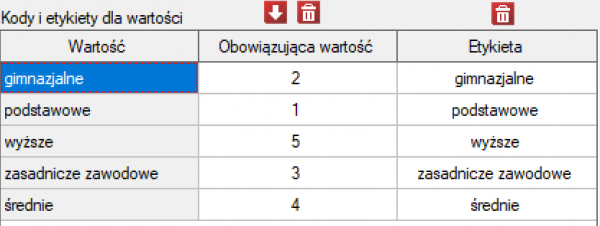
Hipotezy:


Wartość 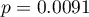 , co w porównaniu z poziomem istotności
, co w porównaniu z poziomem istotności  =0.05 świadczy o prawdziwości hipotezy alternatywnej mówiącej o występowaniu trendu.
=0.05 świadczy o prawdziwości hipotezy alternatywnej mówiącej o występowaniu trendu.
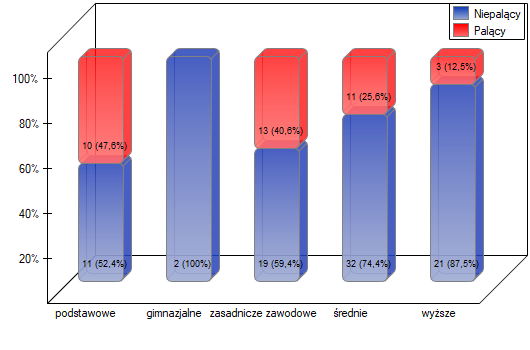
Jak wynika z wykresu czym osoby są bardziej wykształcone, tym rzadziej palą. Jednak wynik uzyskany przez osoby o wykształceniu gimnazjalnym odbiega od tego trendu. Ponieważ wykształcenie gimnazjalne dotyczy tylko dwóch osób, nie miało to dużego wpływu na rysujący się trend. Ze względu na bardzo małą liczność tej grupy postanowiono analizę powtórzyć dla połączonych kategorii wykształcenia podstawowego i gimnazjalnego.
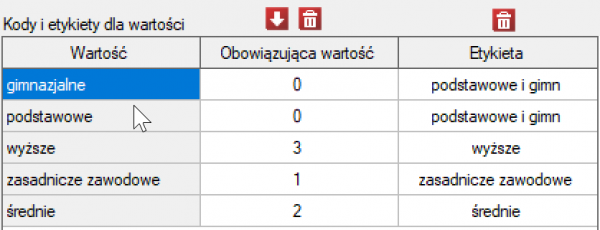
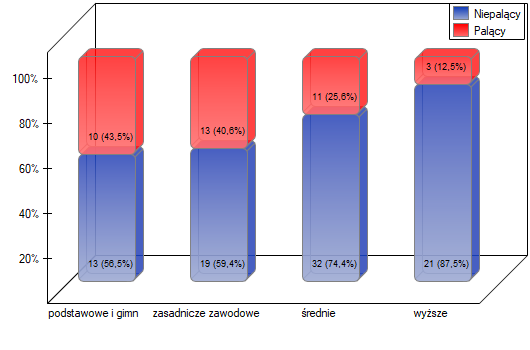
Uzyskano ponownie niewielką wartość 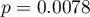 i potwierdzenie istotnego statystycznie trendu.
i potwierdzenie istotnego statystycznie trendu.
Z powodu spadku oglądalności pewnego serialu telewizyjnego przeprowadzono badanie opinii widzów tego serialu. W tym celu przepytano 100 osób, które rozpoczęły oglądanie serialu w ostatnim czasie i 300, które oglądają systematycznie serial od początku. Zapytano ich między innymi o ocenę stopnia zaabsorbowania widza losami bohaterów. Wyniki zapisano w tabeli poniżej:
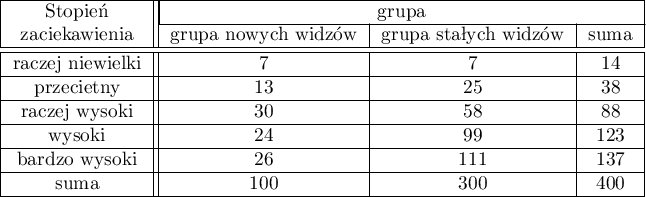
Nowi widzowie stanowią 25% badanych. Taka proporcja nie utrzymuje się jednak dla każdej kategorii „stopnia zaciekawienia” ale przedstawia się następująco:
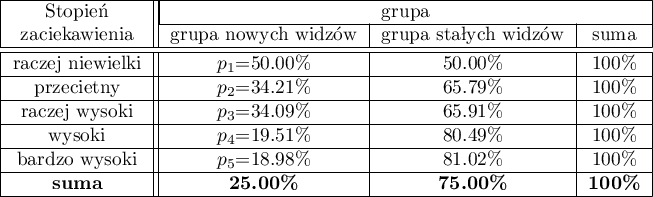
Hipotezy:
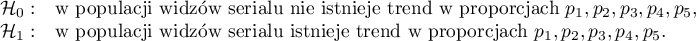
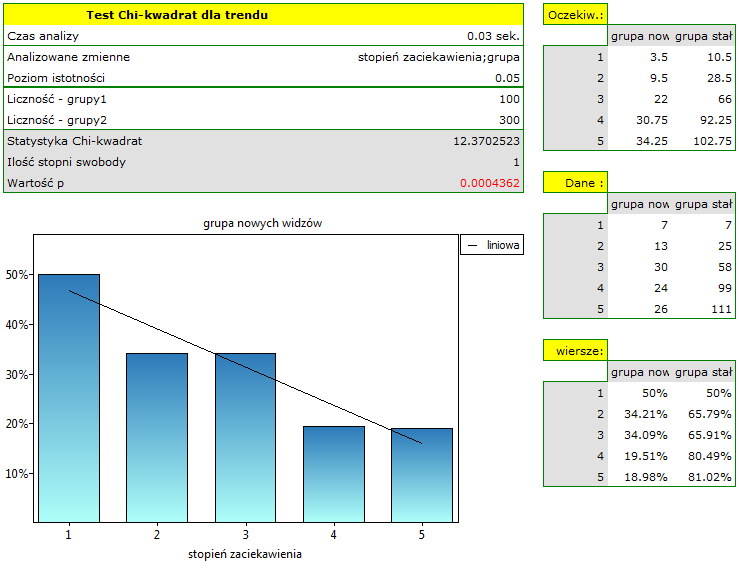
Wartość 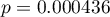 , co w porównaniu z poziomem istotności
, co w porównaniu z poziomem istotności  =0.05 świadczy o prawdziwości hipotezy alternatywnej mówiącej o występowaniu trendu w proporcjach
=0.05 świadczy o prawdziwości hipotezy alternatywnej mówiącej o występowaniu trendu w proporcjach 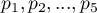 . Jak wynika z tabeli kontyngencji wartości procentowych wyliczanych z sumy kolumn, jest to trend malejący (im grupa widzów jest bardziej zainteresowana losami bohaterów serialu, tym mniejszą jej część stanowią nowi widzowie).
. Jak wynika z tabeli kontyngencji wartości procentowych wyliczanych z sumy kolumn, jest to trend malejący (im grupa widzów jest bardziej zainteresowana losami bohaterów serialu, tym mniejszą jej część stanowią nowi widzowie).
pl/statpqpl/porown2grpl/nparpl/trendpl.txt · ostatnio zmienione: 2022/01/23 21:17 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


