Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
pl:statpqpl:hotelingpl:hotelling2nzalcorrpl
Test T-kwadrat Hotellinga dla grup niezależnych z korektą dla różnych wariancji
Poprawka dotyczy testu T-kwadrat Hotellinga dla grup niezależnych i jest wyliczana wówczas, gdy wariancje badanych zmiennych w obu populacjach są różne.
Statystyka testowa ma postać:
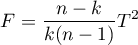
gdzie:
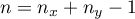 ,
,
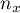 ,
, 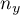 - liczności pierwszej i drugiej próby (liczności poszczególnych zmiennych równe) ,
- liczności pierwszej i drugiej próby (liczności poszczególnych zmiennych równe) ,
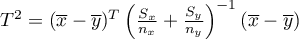 - pierwotna statystyka testowa Hotellinga o rozkładzie
- pierwotna statystyka testowa Hotellinga o rozkładzie  (zalecana dla prób o dużych licznościach),
(zalecana dla prób o dużych licznościach),
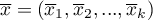 - średnie zmiennych w próbie pierwszej,
- średnie zmiennych w próbie pierwszej,
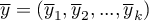 - średnie zmiennych w próbie drugiej,
- średnie zmiennych w próbie drugiej,
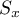 ,
, 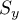 - macierz kowariancji dla pierwszej i drugiej próby.
- macierz kowariancji dla pierwszej i drugiej próby.
Statystyka ta podlega rozkładowi F Snedecora z  i
i 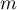 stopniami swobody (gdzie
stopniami swobody (gdzie 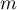 to liczba stopni swobody skorygowana ze względu na różne wariancje).
to liczba stopni swobody skorygowana ze względu na różne wariancje).
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Gdy po wykonanej analizie szukamy zmiennych, których dotyczą różnice, wyznaczamy jednoczesne przedziały ufności dla różnic średnich
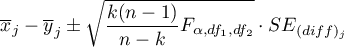
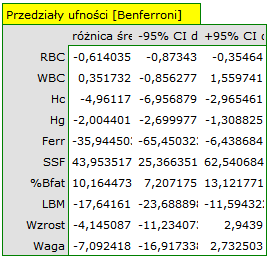
lub przedziały z poprawką Bonferroniego, w celu sprawdzenia czy znajduje się w nich wartość 0. Jeśli bowiem różnica może wynosić 0 to oznacza, że w rzeczywistości różnica pomiędzy badanymi wartościami może nie istnieć. Stosując tą metodę należy pamiętać, że wyznaczone przedziały nie uwzględniają powiązań pomiędzy zmiennymi (które uwzględnia test Hotellinga) a jedynie wielokrotne testowanie.
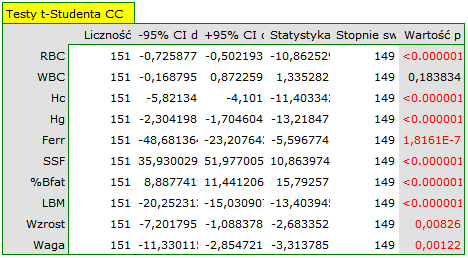
Szukając zmiennych, których dotyczą różnice możemy również zastosować podejście jednowymiarowe. Wykonujemy wówczas porównania testem t-Studenta z korektą Cochrana-Coxa oddzielnie dla poszczególnych zmiennych. Niestety, nie uwzględnimy tym samym wzajemnych powiązań, ale uzyskane wartości  testu
testu  -Studenta możemy skorygować w dziale Wielokrotne porównania.
-Studenta możemy skorygować w dziale Wielokrotne porównania.
Uwaga!
Zasada działania testu Hotellinga jest tożsama z budową „wielowymiarowych elips” przedziałów ufności wokół centrów wyznaczonych przez średnie (patrz przykład interpretacji elipsy testu Hotellinga dla pojedynczej próby). Przez co, stosując analizę jednowymiarową (nie uwzględniającą wzajemnych powiązań między zmiennymi) często nie jesteśmy w stanie uzyskać tożsamych wyników.
Okno z ustawieniami opcji testu Hotellinga dla grup niezależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→T-kwadrat Hotellinga dla grup niezależnych.
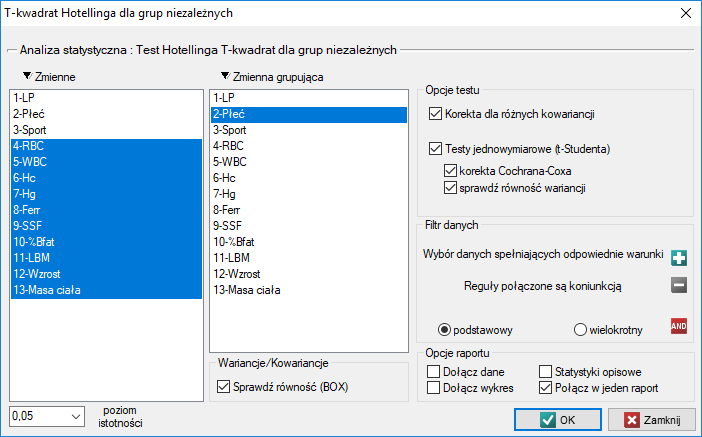
Przebadano grupę sportowców by uzyskać informację o parametrach zdrowotnych takich jak:
![LaTeX \begin{tabular}{ll}
RBC - Liczba czerwonych krwinek, & SSF - Suma fałdów skórno-tłuszczowych [mm],\\
WBC - Liczba białych krwinek, & \% Bfat - Zawartość tłuszczu w organizmie,\\
Hc - Hematokryt [\%], & LBM - Beztłuszczowa masa ciała [kg],\\
Hg - Hemoglobina [g/dl], & Wzrost [cm],\\
Ferr - Ferrytyna [µg/l], & Masa ciała [kg].
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img5ad8771ed09589cf5bd45a6e79dcdc36.png)
Chcemy wiedzieć, czy kobiety i mężczyźni, uprawiający zawodowo analizowane rodzaje sportu, różnią się poziomami tych parametrów.
Hipotezy:

Ze względu na różnice dotyczące kowariancji analizowanych parametrów (wartość  testu Boxa
testu Boxa 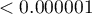 ) analizę przeprowadzamy przy włączonej korekcie różnych macierzy kowariancji.
) analizę przeprowadzamy przy włączonej korekcie różnych macierzy kowariancji.

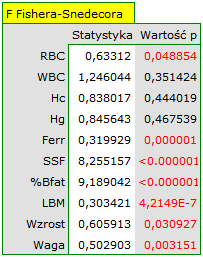
Uzyskany wynik skorygowanej statystyki Hotellinga jest przedstawiony poniżej.
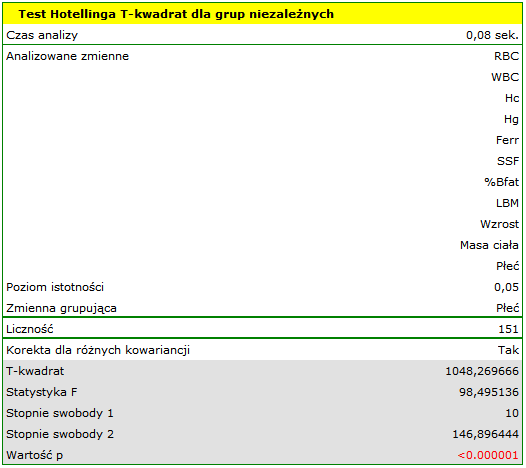
Porównując wartość 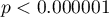 z poziomem istotności
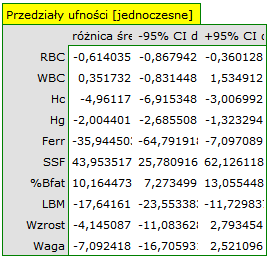
z poziomem istotności  stwierdzamy, że mężczyźni i kobiety w badanej populacji mają inne wartości średnie analizowanych parametrów. Według jednoczesnych przedziałów ufności (oraz według przedziałów z korektą Bonferroniego) różnice dotyczą:
stwierdzamy, że mężczyźni i kobiety w badanej populacji mają inne wartości średnie analizowanych parametrów. Według jednoczesnych przedziałów ufności (oraz według przedziałów z korektą Bonferroniego) różnice dotyczą:
RBC - średnio kobiety uzyskują niższe wartości,
Hc - średnio kobiety uzyskują niższe wartości,
Hg - średnio kobiety uzyskują niższe wartości,
Ferr - średnio kobiety uzyskują niższe wartości,
SSF - średnio mężczyźni uzyskują niższe wartości,
% Bfat - średnio mężczyźni uzyskują niższe wartości,
LBM - średnio kobiety uzyskują niższe wartości.
Pozostałe parametry czyli WBC, wzrost i masa ciała nie różnią się istotnie.
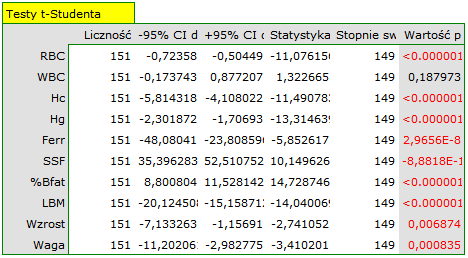
Podejście jednowymiarowe, choć nie uwzględniające wielokrotnego testowania ani wzajemnych powiązań, ze względu na swoją prostotę wykorzystywane jest najczęściej. Jego wyniki wskazują że różnice dotyczą wszystkich badanych parametrów za wyjątkiem WBC. Przy czym wyniki testu t-Studenta interpretujemy po uwzględnieniu korekty Cochrana-Coxa lub bez tej korekty, w zależności od spełnienia założenia równości wariancji (wynik testu Fishera-Snedecora). Chcąc uwzględnić wielokrotne testowania należałoby w tym przypadku zastosować jedną z korekt wartości p, opisanych w dziale Wielokrotne porównania.
pl/statpqpl/hotelingpl/hotelling2nzalcorrpl.txt · ostatnio zmienione: 2014/12/20 16:35 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

