Spis treści
Testy nieparametryczne
ANOVA Kruskala-Wallisa
Jednoczynnikowa analiza wariancji dla rang Kruskala-Walisa, czyli ANOVA Kruskala-Wallisa (ang. Kruskal-Wallis one-way analysis of variance by ranks) opisana przez Kruskala (1952)1) oraz Kruskala i Wallisa (1952)2) jest rozszerzeniem testu U-Manna-Whitneya na więcej niż dwie populacje. Test ten służy do weryfikacji hipotezy o braku przesunięcia porównywanych rozkładów tzn. najczęsciej nieistotności różnic pomiędzy medianami badanej zmiennej w kilku (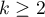 ) populacjach (przy czym zakładamy, że rozkłady zmiennej są sobie bliskie - porównanie wariancji rang można sprawdzić testem dla rang Conovera).
) populacjach (przy czym zakładamy, że rozkłady zmiennej są sobie bliskie - porównanie wariancji rang można sprawdzić testem dla rang Conovera).
Dodatkowe analizy:
- możliwe jest testowanie trendu w ułożeniu badanych grup poprzez wykonanie testu Jonckheere-Terpstra dla trendu.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości średnich rang dla kolejnych populacji lub są upraszczane do median:
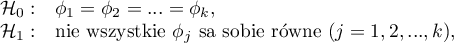
gdzie:
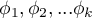 to rozkłady badanej zmiennej w populacjach, z których pobrano próby.
to rozkłady badanej zmiennej w populacjach, z których pobrano próby.
Statystyka testowa ma postać:
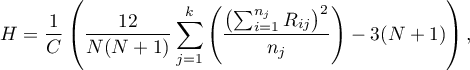
gdzie:
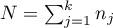 ,
,
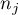 - liczności prób dla
- liczności prób dla  ,
,
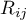 - rangi przypisane do wartości zmiennej, dla
- rangi przypisane do wartości zmiennej, dla 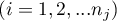 ,
,  ,
,
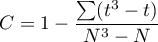 - korekta na rangi wiązane,
- korekta na rangi wiązane,
 - liczba przypadków wchodzących w skład rangi wiązanej.
- liczba przypadków wchodzących w skład rangi wiązanej.
Wzór na statystykę testową 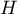 zawiera poprawkę na rangi wiązane
zawiera poprawkę na rangi wiązane  . Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 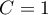 ).
).
Statystyka 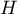 ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru:
ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru: 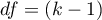 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC przeprowadzone zostało w rozdziale dotyczącym jednoczynnikowej analizy wariancji.
Dla porównań prostych, zarówno równolicznych jak i różnolicznych grup.
Test Dunna (Dunn 19643)) zawiera poprawkę na rangi wiązane (Zar 20104)) i jest testem korygowanym ze względu na wielokrotne testowanie. Najczęściej wykorzystuje się tu korektę Bonferroniego lub Sidaka, chociaż dostępne są również inne, nowsze korekty opisane szerzej w dziale Wielokrotne porównania.
Przykład - porównania proste (porównanie pomiędzy sobą 2 wybranych median / średnich rang):
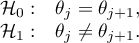
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
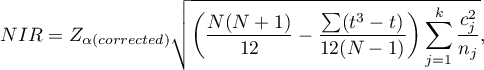
gdzie:

 liczba przypadków wchodzących w skład rangi wiązanej
liczba przypadków wchodzących w skład rangi wiązanej
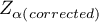 - to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności
- to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności  skorygowanego o liczbę możliwych porównań prostych
skorygowanego o liczbę możliwych porównań prostych  zgodnie z wybraną poprawką.
zgodnie z wybraną poprawką.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
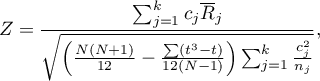
gdzie:
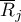 - średnia rang
- średnia rang  -tej grupy, dla
-tej grupy, dla  ,
,
Wzór na statystykę testową  zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, ponieważ
zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, ponieważ 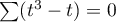 ).
).
Statystyka ta ma asymptotycznie (dla dużych liczności próby) rozkład normalny, a wartość p jest korygowana o liczbę możliwych porównań prostych  zgodnie z wybraną poprawką.
zgodnie z wybraną poprawką.
Nieparametryczny odpowiednik LSD Fishera5), stosowany dla porównań prostych zarówno równolicznych jak i różnolicznych grup.
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
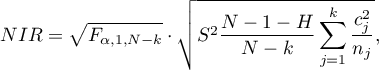
gdzie:
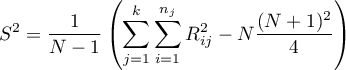
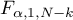 to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności
to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności  oraz dla stopni swobody odpowiednio: 1 i
oraz dla stopni swobody odpowiednio: 1 i 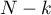 .
.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
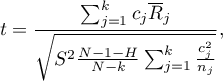
gdzie:
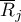 - średnia rang
- średnia rang  -tej grupy, dla
-tej grupy, dla  ,
,
Statystyka ta podlega rozkładowi t-Studenta z 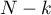 stopniami swobody.
stopniami swobody.
Okno z ustawieniami opcji ANOVA Kruskala-Wallisa wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Kruskala-Wallisa lub poprzez Kreator.
Przykład (satysfakcjaZpracy.pqs)
Przepytano grupę 120 osób, dla których wykonywane zajęcie jest ich pierwszą pracą uzyskaną po otrzymaniu odpowiedniego wykształcenia. Ankietowani oceniali satysfakcję z wykonywanej pracy w pięciostopniowej skali, gdzie:
1- praca niesatysfakcjonująca,
2- praca dająca niewielką satysfakcję,
3- praca dająca przeciętny poziom satysfakcji,
4- praca dająca dość dużą satysfakcję ,
5- praca bardzo satysfakcjonująca.
Sprawdzimy czy poziom deklarowanej satysfakcji z pracy nie zmienia się dla poszczególnych kategorii wykształcenia.
Hipotezy:

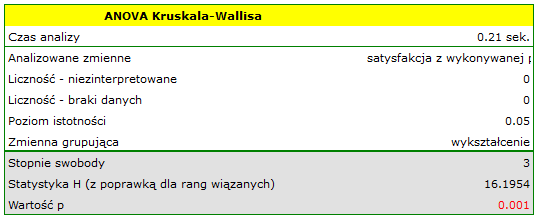
Uzyskana wartość 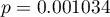 świadczy o istotnej różnicy poziomu satysfakcji pomiędzy porównywanymi kategoriami wykształcenia. Przeprowadzona analiza POST-HOC Dunna z korektą Bonferroniego wskazuje, że istotne różnice dotyczą osób z wykształceniem podstawowym i średnim oraz z wykształceniem podstawowym i wyższym. Nieco więcej różnic możemy potwierdzić wybierająć silniejszy POST-HOC Conover-Iman.
świadczy o istotnej różnicy poziomu satysfakcji pomiędzy porównywanymi kategoriami wykształcenia. Przeprowadzona analiza POST-HOC Dunna z korektą Bonferroniego wskazuje, że istotne różnice dotyczą osób z wykształceniem podstawowym i średnim oraz z wykształceniem podstawowym i wyższym. Nieco więcej różnic możemy potwierdzić wybierająć silniejszy POST-HOC Conover-Iman.
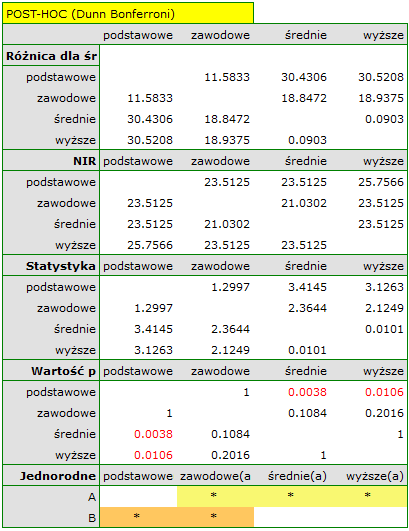
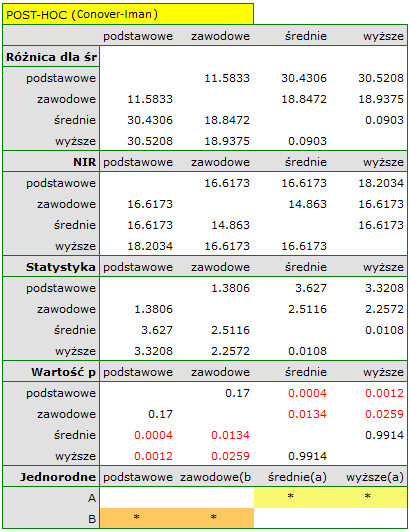
Na wykresie przedstawiającym mediany i kwartyle możemy zobaczyć grupy jednorodne wyznaczone przez test POST-HOC. Jeśli zdecydujemy się na przedstawienie wyników Dunna z korektą Bonferroniego zobaczymy dwie grupy jednorodne, które nie są zupełnie odrębne, tzn. grupę (a) - osoby słabiej oceniające satysfakcję z pracy i grupę (b)- osoby lepiej oceniające tę satysfakcję. Wykształcenie zawodowe przynależy do obydwu tych grup, co oznacza, że osoby z tym wykształceniem oceniają satysfakcję z pracy dość różnorodnie. Ten sam opis grup jednorodnych możemy znaleźć w wynikach testów POST-HOC.
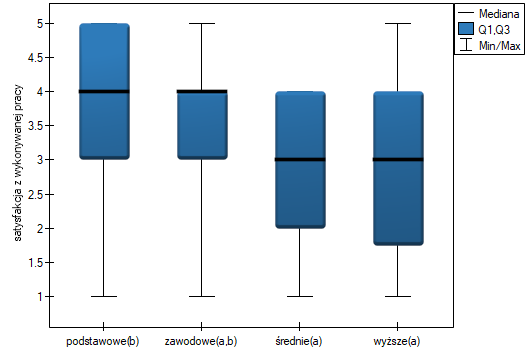
Dokładny opis danych możemy przedstawić wybierając w oknie analizy statystyki opisowe 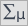 i wskazując na dodanie do opisu liczności i procentów.
i wskazując na dodanie do opisu liczności i procentów.
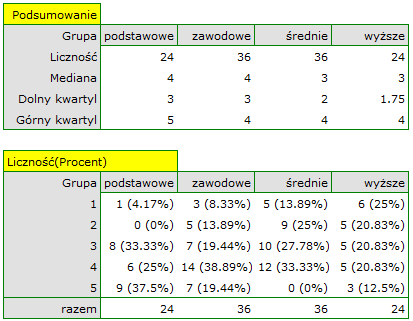
Rozkład odpowiedzi możemy też przedstawić na wykresie liczności.
Test Jonckheere-Terpstra dla trendu
Test Jonckheere-Terpstra dla trendu (ang. the Jonckheere-Terpstra test for ordered alternatives) opisany niezależnie przez Jonckheere (1954) 6) i Terpstra (1952)7) może być wyliczany w takiej samej sytuacji jak ANOVA Kruskala-Wallisa, gdyż bazuje na tych samych założeniach. Test Jonckheere-Terpstra inaczej jednak ujmuje hipotezę alternatywną - wskazując w niej na istnienie trendu dla kolejnych populacji.
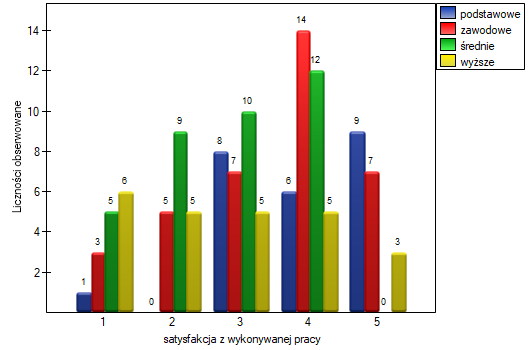
Hipotezy są upraszczane do median:
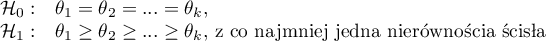
Uwaga!
Określenie: „z co najmniej jedną nierównością ścisłą” zapisane w hipotezie alternatywnej tego testu oznacza, że co najmniej mediana jednej populacji powinna być większa niż mediana innej populacji w kolejności określonej.
Statystyka testowa ma postać:
![LaTeX \begin{displaymath}
Z=\frac{L-\left[\frac{N^2-\sum_{j=1}^kn_j^2}{4}\right]}{SE}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img90c514ede7a37557872f285e3a796486.png)
gdzie:
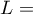 - suma wartości
- suma wartości 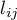 uzyskanych dla każdej pary porównywanych populacji,
uzyskanych dla każdej pary porównywanych populacji,
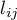 - liczba wyników wyższych niż zadana wartość w grupie występującej w następnej kolejności,
- liczba wyników wyższych niż zadana wartość w grupie występującej w następnej kolejności,
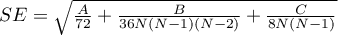 ,
,
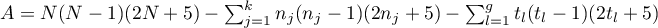 ,
,
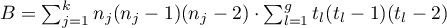 ,
,
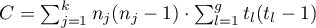 ,
,
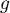 - liczba grup różnych rang wiązanych,
- liczba grup różnych rang wiązanych,
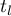 -liczba przypadków wchodzących w skład rangi wiązanej,
-liczba przypadków wchodzących w skład rangi wiązanej,
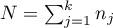 ,
,
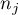 - liczności prób dla
- liczności prób dla  .
.
Uwaga!
By można było przeprowadzić analizę trendu, należy wskazać oczekiwaną kolejność populacji przypisując im kolejne liczby naturalne.
Wzór na statystykę testową  zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych wzór na statystykę testową sprowadza się do oryginalnej formuły Jonckheere-Terpstra nie zawierającej tej poprawki).
zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych wzór na statystykę testową sprowadza się do oryginalnej formuły Jonckheere-Terpstra nie zawierającej tej poprawki).
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Przy znanym oczekiwanym kierunku trendu, hipoteza alternatywna jest jednostronna i interpretacji podlega jednostronna wartość  . Interpretacja dwustronnej wartości
. Interpretacja dwustronnej wartości  oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość
oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

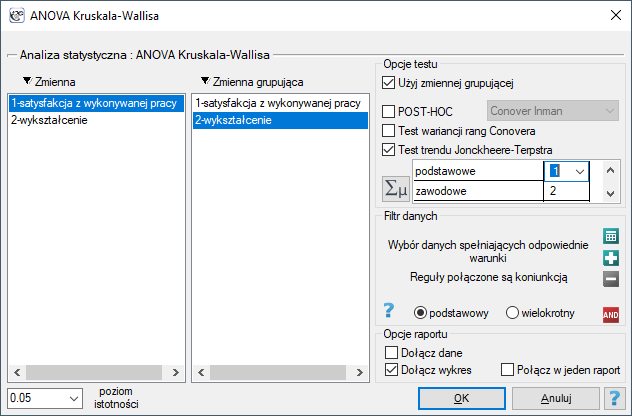
Okno z ustawieniami opcji testu Jonckheere-Terpstra wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Kruskala-Wallisa lub poprzez Kreator.
Pprzykład c.d. (plik satysfakcjaZpracy.pqs)
Podejrzewa się, że osoby lepiej wykształcone mają wysokie wymagania zawodowe, co może zmniejszać poziom satysfakcji z pierwszej pracy, która często takich wymagań nie spełnia. Dlatego też warto przeprowadzić analizę trendu.
Hipotezy:
W tym celu wznawiamy analizę przyciskiem  , zaznaczamy opcję
, zaznaczamy opcję Test trendu Jonckheere-Terpstra i kolejnym kategoriom wykształcenia przypisujemy kolejne liczby naturalne.
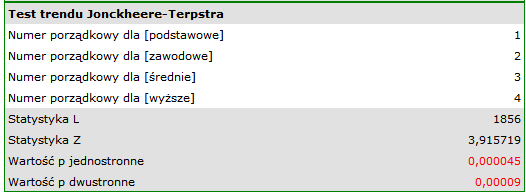
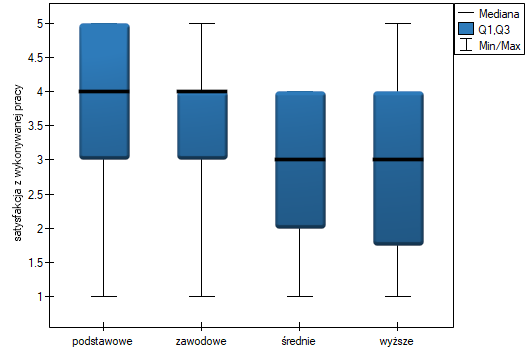
Uzyskana jednostronna wartość 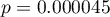 i jest mniejsza niż zadany poziom istotności
i jest mniejsza niż zadany poziom istotności  , co przemawia na rzecz rzeczywiście występującego trendu zgodnego z oczekiwaniami badacza.
, co przemawia na rzecz rzeczywiście występującego trendu zgodnego z oczekiwaniami badacza.
Istnienie tego trendu możemy również potwierdzić przedstawiając procentowy rozkład uzyskanych odpowiedzi.
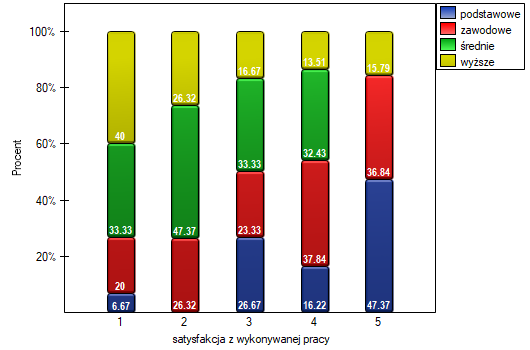
Test wariancji rang Conover
Test kwadratów rang Conovera służy, podobnie jak test Fishera-Snedecora (dla 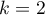 ), test Levene i test Browna-Forsythea (dla
), test Levene i test Browna-Forsythea (dla 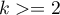 ) do weryfikacji hipotezy podobnym zróżnicowaniu badanej zmiennej w kilku populacjach. Jest on nieparametrycznym odpowiednikiem wskazanych wyżej testów, przez to nie zakłada normalności rozkładu danych i opiera się na rangach 8). Jednak test ten bada zróżnicowanie, a więc odległości do średniej, dlatego podstawowym warunkiem jego stosowania jest:
) do weryfikacji hipotezy podobnym zróżnicowaniu badanej zmiennej w kilku populacjach. Jest on nieparametrycznym odpowiednikiem wskazanych wyżej testów, przez to nie zakłada normalności rozkładu danych i opiera się na rangach 8). Jednak test ten bada zróżnicowanie, a więc odległości do średniej, dlatego podstawowym warunkiem jego stosowania jest:
- pomiar na skali interwałowej,
Hipotezy:
Statystyka testowa ma postać:
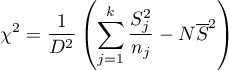
gdzie:
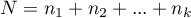 ,
,
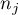 - liczność w poszczególnych grupach,
- liczność w poszczególnych grupach,
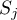 - suma kwadratów rang w
- suma kwadratów rang w  -tej grupie,
-tej grupie,
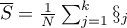 - średnia wszystkich kwadratów rang,
- średnia wszystkich kwadratów rang,
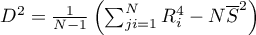 ,
,
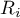 -rangi dla wartości przedstawiających odległość pomiaru od średniej danej grupy.
-rangi dla wartości przedstawiających odległość pomiaru od średniej danej grupy.
Statystyka ta ma rozkład chi-kwadrat z 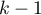 stopniem swobody.
stopniem swobody.
wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji testu wariancji rang Conovera wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Kruskala-Wallisa, opcja testu wariancji rang Conovera lub Statystyka→Testy nieparametryczne→Mann-Whitney, opcja testu wariancji rang Conovera.
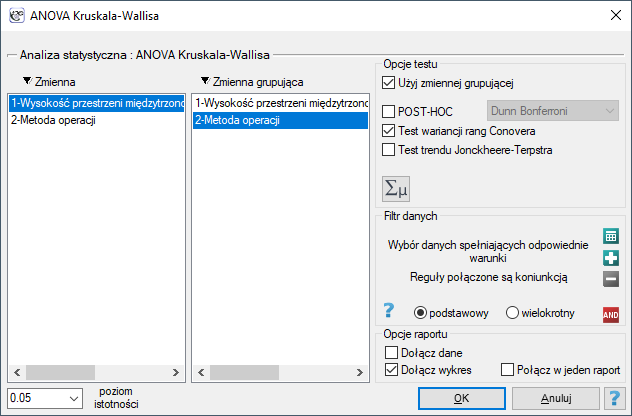
Przygotowano chorych do operacji kręgosłupa. Chorzy będą operowani jedną z trzech metod. Dokonano wstępnego przydziału każdej osoby chorej do poszczególnych typów operacji. Na późniejszym etapie zamierzamy porównywać stan chorych po przebytych operacjach, dlatego zależy nam by grupy chorych były porównywalne. Powinny być podobne min. pod względem wysokości przestrzeni międzytrzonowej (WPMT) przed operacją. Podobieństwo powinno dotyczyć nie tylko wartości przeciętnych ale również zróżnicowania grup.
Sprawdzono rozkład danych.
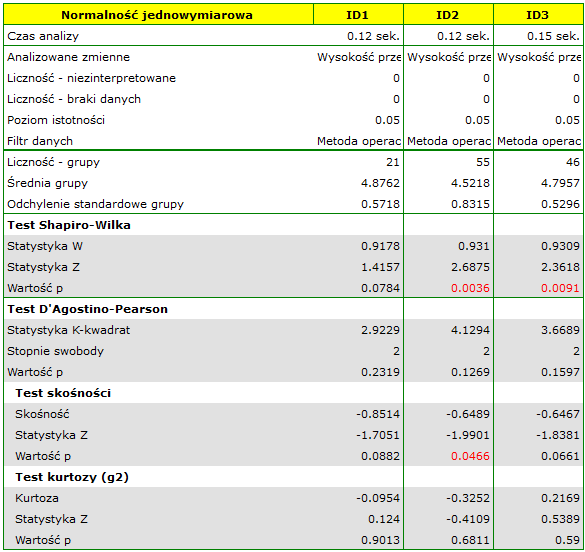
Okazuje się, że w przypadku dwóch metod operacji WPMT wykazuje odstępstwa od normalności, których przyczyną w dużej mierze jest skośność danych. Dalsza analiza porównawcza przeprowadzona zostanie przy pomocy testu Kruskala-Wallisa, by porównać czy poziom WPMT różni się pomiędzy metodami oraz testu Conovera, który wskaże, czy w każdej metodzie rozpiętość wyników WPMT jest podobna.
Hipotezy dla testu wariancji Conovera:
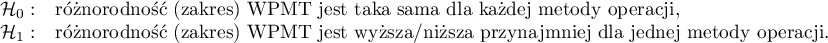
Hipotezy dla testu Kruskala-Wallisa :
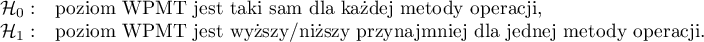
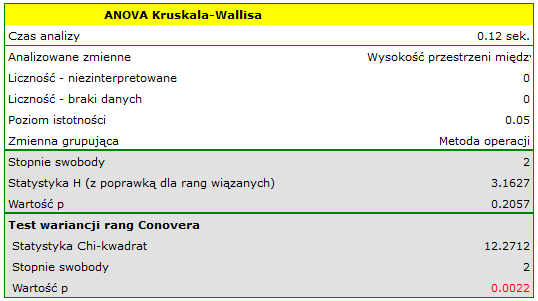
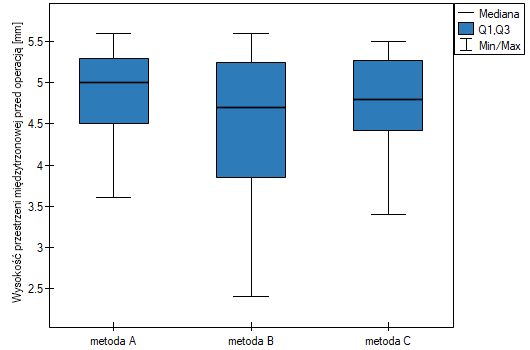
Najpierw interpretacji podlega wartość testu wariancji Conovera, która wskazuje na istotne statystycznie różnice w zakresach porównywanych grup (p=0.0022). Z wykresu możemy wnioskować, że różnice dotyczą głównie grupy 3. Ponieważ wykryto różnice w zakresie WPMT, to interpretacja wyniku testu Kruskala-Wallisa, porównującego poziom WPMT dla tych metod, powinna być ostrożna, gdyż test ten jest wrażliwy na niejednorodność wariancji. Mimo iż test Kruskala-Wallisa nie wykazał istotnych różnic (p=0.2057), to zaleca się by chorych o niskich WPMT (którzy zostali przypisani głównie do operacji metodą B) rozmieścić bardziej równomiernie tzn. by sprawdzić, czy nie można im zaproponować wykonania operacji metodą A lub C. Po ponownym przydziale chorych należy powtórzyć analizę.}
ANOVA Friedmana
Analiza wariancji powtarzanych pomiarów dla rang Friedmana, czyli ANOVA Friedmana (ang. Friedman repeated measures analysis of variance by ranks) opisana została przez Friedmana (1937)9). Test ten stosuje się w sytuacji, gdy pomiarów badanej zmiennej dokonujemy kilkukrotnie (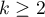 ) w różnych warunkach. Stosowana jest również, gdy dysponujemy rankingami pochodzącymi z różnych źródeł (od różnych sędziów) i dotyczącymi kilku (
) w różnych warunkach. Stosowana jest również, gdy dysponujemy rankingami pochodzącymi z różnych źródeł (od różnych sędziów) i dotyczącymi kilku ( ) obiektów a zależy nam na ocenie zgodności tych rankingów.
) obiektów a zależy nam na ocenie zgodności tych rankingów.
Iman Davenport (198010)) pokazał, że w wielu przypadkach statystka Friedmana jest nadmiernie konserwatywna i dokonał pewnej jej modyfikacji. Modyfikacja ta jest nieparametrycznym odpowiednikiem ANOVA powtarzanych pomiarów co sprawia, że jest obecnie rekomendowana do stosowania w zastępstwie tradycyjnej statystyki Friedmana.
Dodatkowe analizy:
- możliwe jest uwzględnienie braków danych poprzez opcje
Akceptuj braki danych, wyliczając ANOVA Durbina lub ANOVA Skillings-Mack; - możliwe jest testowanie trendu w ułożeniu badanych grup poprzez wykonanie testu Page dla trendu.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości sumy rang dla kolejnych pomiarów lub są upraszczane do median:
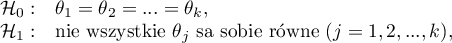
gdzie:
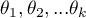 mediany badanej cechy w kolejnych pomiarach z badanej populacji.
mediany badanej cechy w kolejnych pomiarach z badanej populacji.
Wyznacza się dwie statystyki testowe: statystykę Friedmana i modyfikację Imana-Davenport tej statystyki.
Statystyka Friedmana ma postać:
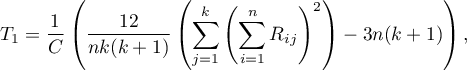
gdzie:

 liczność próby,
liczność próby,
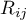
 rangi przypisane kolejnym pomiarom
rangi przypisane kolejnym pomiarom  , oddzielnie dla każdego z badanych obiektów
, oddzielnie dla każdego z badanych obiektów 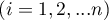 ,
,
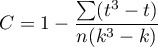
 korekta na rangi wiązane,
korekta na rangi wiązane,

 liczba przypadków wchodzących w skład rangi wiązanej.
liczba przypadków wchodzących w skład rangi wiązanej.
Modyfikacjia Imana-Davenport statystyki Friedmana ma postać:
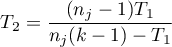
Wzór na statystykę 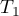 i
i 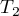 zawiera poprawkę na rangi wiązane
zawiera poprawkę na rangi wiązane  . Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 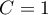 ).
).
Statystyka 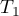 ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z
ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 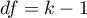 stopniami swobody.
stopniami swobody.
Statystyka 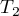 podlega rozkładowi F Snedecora z
podlega rozkładowi F Snedecora z 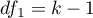 i
i  stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC przeprowadzone zostało w rozdziale dotyczącym jednoczynnikowej analizy wariancji.
Stosowany dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
Test Dunna (Dunn 196411)) jest testem korygowanym ze względu na wielokrotne testowanie. Najczęściej wykorzystuje się tu korektę Bonferroniego lub Sidaka, chociaż dostępne są również inne, nowsze korekty opisane szerzej w dziale Wielokrotne porównania.
Przykład - porównania proste (porównanie pomiędzy sobą 2 wybranych median / średnich rang):
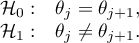
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
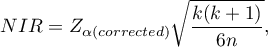
gdzie:
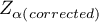 - to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności
- to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności  skorygowanego o liczbę możliwych porównań prostych
skorygowanego o liczbę możliwych porównań prostych  zgodnie z wybraną poprawką.
zgodnie z wybraną poprawką.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
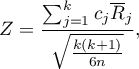
gdzie:
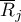
 średnia rang
średnia rang  -tego pomiaru, dla
-tego pomiaru, dla  ,
,
Statystyka ta ma asymptotycznie (dla dużych liczności próby) rozkład normalny, a wartość p jest korygowana o liczbę możliwych porównań prostych zgodnie z wybraną poprawką.
Nieparametryczny odpowiednik LSD Fishera12), stosowany dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
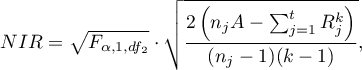
gdzie:
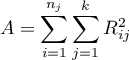
 suma kwadratów dla rang,
suma kwadratów dla rang,
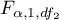 to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności
to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności  oraz dla stopni swobody odpowiednio: 1 i
oraz dla stopni swobody odpowiednio: 1 i 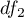 .
.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
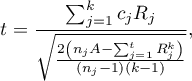
gdzie:
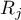 - suma rang
- suma rang  -tego pomiaru, dla
-tego pomiaru, dla  ,
,
Statystyka ta podlega rozkładowi t-Studenta z 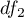 stopniami swobody.
stopniami swobody.
Okno z ustawieniami opcji ANOVA Friedmana wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Friedmana (możliwość braków danych) lub poprzez Kreator.
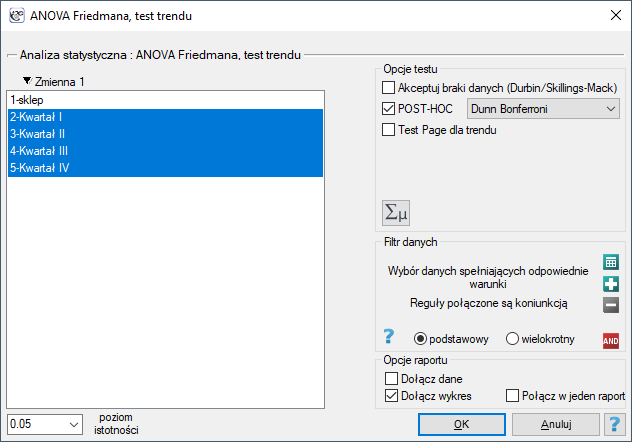
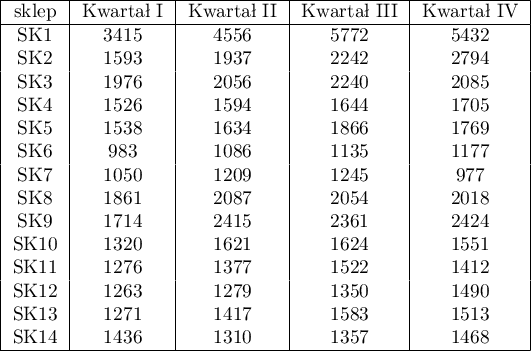
Badano kwartalną wielkość sprzedaży pewnego batonu czekoladowego w 14 losowo wybranych marketach. Badanie rozpoczęto w styczniu a zakończono w grudniu. W czasie drugiego kwartału trwała intensywna billboardowa kampania reklamowa tego produktu. Sprawdzimy, czy kampania miała wpływ na wielkość sprzedaży reklamowanego batonu.
Hipotezy:

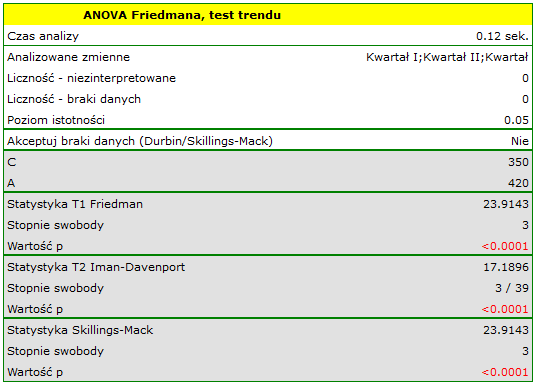
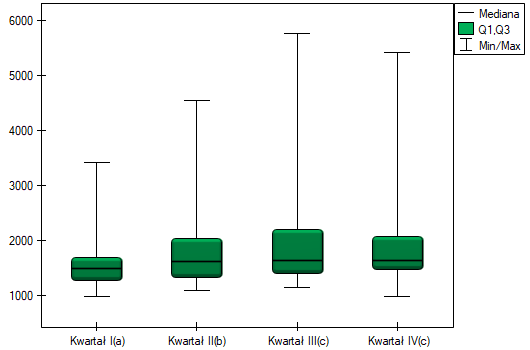
Porównując wartość p testu Friedmana (jak i wartość p korekty Iman-Davenport testu Friedmana) z poziomem istotności  , stwierdzamy, że sprzedaż batonu nie jest taka sama w każdym kwartale. Wykonana analiza POST-HOC Dunna z korektą Bonferroniego wskazuje na różnice wielkości sprzedaży dotyczące kwartału I i III oraz I i IV, a analogiczna analiza przeprowadzona silniejszym testem Conover-Iman wskazuje na różnice pomiędzy wszystkimi kwartałami za wyjątkiem kwartału III i IV.
, stwierdzamy, że sprzedaż batonu nie jest taka sama w każdym kwartale. Wykonana analiza POST-HOC Dunna z korektą Bonferroniego wskazuje na różnice wielkości sprzedaży dotyczące kwartału I i III oraz I i IV, a analogiczna analiza przeprowadzona silniejszym testem Conover-Iman wskazuje na różnice pomiędzy wszystkimi kwartałami za wyjątkiem kwartału III i IV.
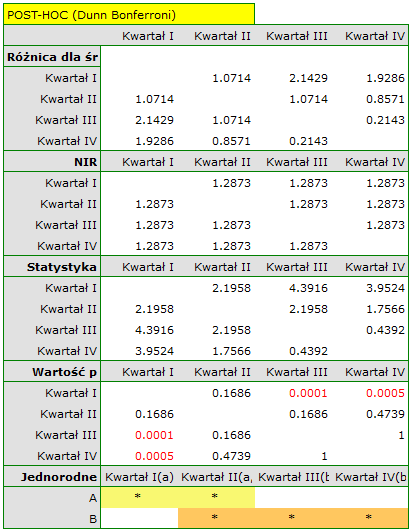
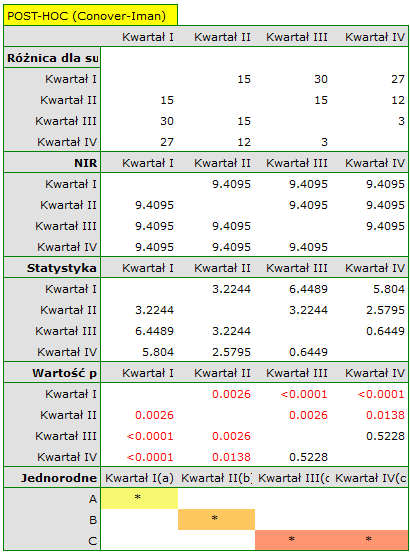
Na wykresie przedstawiliśmy grupy jednorodne wyznaczone testem Conover-Iman.
Dokładny opis danych możemy przedstawić wybierając w oknie analizy statystyki opisowe  .
.
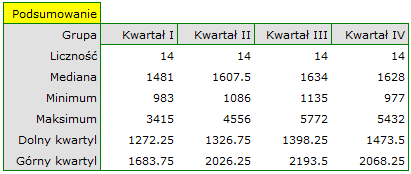
Gdyby dane były opisane skalą porzadkową o niewielu kategoriach, warto by było przedstawić je rownież w licznościach i procentach. W naszym przykładzie nie byłaby to dobra metoda opisu.
Test Page dla trendu
Test Page dla trendu (ang. the Page test for ordered alternative) opisany w roku 1963 przez Page E. B. 13) może być wyliczany w takiej samej sytuacji jak ANOVA Friedmana, gdyż bazuje na tych samych założeniach. Test Page inaczej jednak ujmuje hipotezę alternatywną - wskazując w niej na istnienie trendu w kolejnych pomiarach.
Hipotezy dotyczą równości sumy rang dla kolejnych pomiarów lub są upraszczane do median:
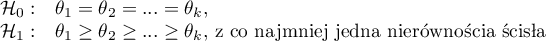
Uwaga!
Określenie: „z co najmniej jedną nierównością ścisłą” zapisane w hipotezie alternatywnej tego testu oznacza, że co najmniej jedna mediana powinna być większa niż mediana innej grupy pomiarów w kolejności określonej.
Statystyka testowa ma postać:
![LaTeX \begin{displaymath}
Z=\frac{L-\left[\frac{nk(k+1)^2}{4}\right]}{\sqrt{\frac{n(k^3-k)^2}{144(k-1)}}}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/imgd8f373e9725654f26c78c01931a87148.png)
gdzie:
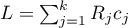 ,
,
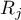
 suma rang
suma rang  -tego pomiaru,
-tego pomiaru,
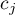
 waga dla
waga dla  -tego pomiaru informująca o naturalnym porządku tego pomiaru w śród innych pomiarów (wagi to kolejne liczby naturalne).
-tego pomiaru informująca o naturalnym porządku tego pomiaru w śród innych pomiarów (wagi to kolejne liczby naturalne).
Uwaga!
By można było przeprowadzić analizę trendu, należy wskazać oczekiwane uporządkowanie pomiarów przypisując kolejne liczby naturalne kolejnym grupom pomiarowym. Liczby te w analizie traktowane są jako wagi 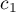 ,
, 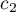 , …,
, …, 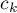 .
.
Wzór na statystykę testową  nie zawiera poprawki na rangi wiązane, przez co staje się nieco bardziej konserwatywny, gdy rangi wiązane występują. Jednakże stosowanie korekty na rangi wiązane w przypadku tego testu nie jest rekomendowane.
nie zawiera poprawki na rangi wiązane, przez co staje się nieco bardziej konserwatywny, gdy rangi wiązane występują. Jednakże stosowanie korekty na rangi wiązane w przypadku tego testu nie jest rekomendowane.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Przy znanym oczekiwanym kierunku trendu, hipoteza alternatywna jest jednostronna i interpretacji podlega jednostronna wartość  . Interpretacja dwustronnej wartości
. Interpretacja dwustronnej wartości  oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość
oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji testu Page wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Friedmana (możliwość braków danych) lub poprzez Kreator.
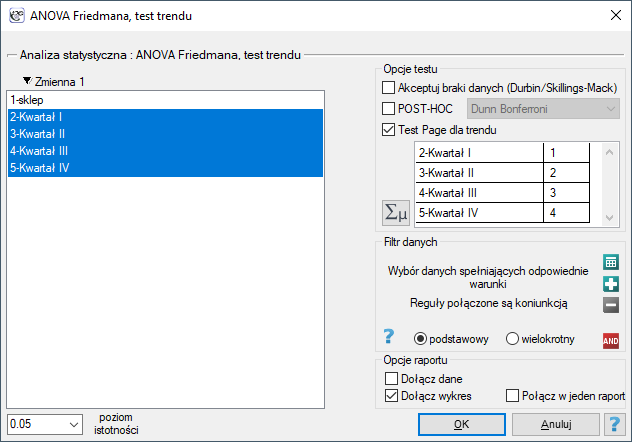
Przykład c.d. (plik baton.pqs)
Oczekiwanym skutkiem prowadzenia przez firmę intensywnej kampanii reklamowej jest stały wzrost sprzedaży oferowanego batonu.
Hipotezy:
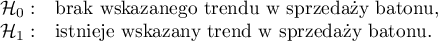
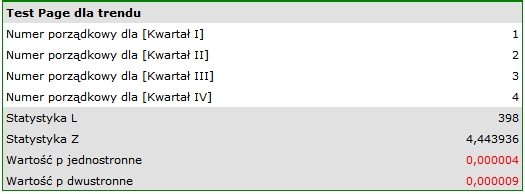
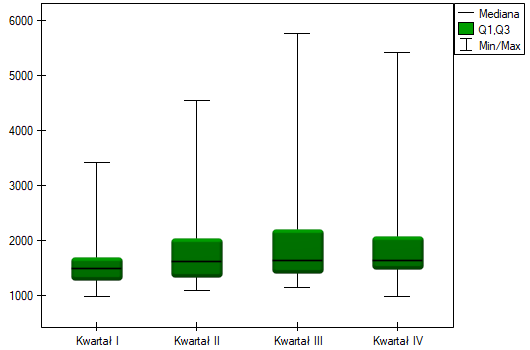
Porównując jednostronną wartość 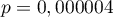 z poziomem istotności
z poziomem istotności  , stwierdzamy, że kampania przyniosła oczekiwany trend wzrostu sprzedaży produktu.
, stwierdzamy, że kampania przyniosła oczekiwany trend wzrostu sprzedaży produktu.
ANOVA Durbina (brakujących danych)
Analiza wariancji powtarzanych pomiarów dla rang Durbina została zaproponowana przez Durbina (1951)14). Test ten stosuje się w sytuacji, gdy pomiarów badanej zmiennej dokonujemy kilkukrotnie - czyli w podobnej sytuacji w jakiej stosowana jest ANOVA Friedmana. Oryginalny test Durbina i test Friedmana dają ten sam wynik w sytuacji, gdy dysponujemy kompletnym zestawem danych. Test Durbina ma jednak pewną przewagę - można go również wyliczać dla niekompletnego zestawu danych. Przy czym braki danych nie mogą być zlokalizowane dowolnie, ale dane muszą tworzyć tzw. zbalansowany i niekompletny blok, czyli:
- liczba pomiarów dla każdego obiektu wynosi
 (
(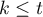 ),
), - każdy pomiar dokonywany jest na
 obiektach (
obiektach (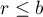 ),
), - liczba obiektów dla których wykonano jednocześnie tą sama parę pomiarów jest stała i wynosi
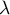 .
.
gdzie:
 - łączna liczba rozpatrywanych pomiarów,
- łączna liczba rozpatrywanych pomiarów,
 - łączna liczba badanych obiektów
- łączna liczba badanych obiektów
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości sumy rang dla kolejnych pomiarów (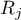 ) lub są upraszczane do median (
) lub są upraszczane do median (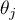 ):
):
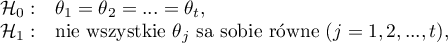
Wyznacza się dwie statystyki testowe o następującej postaci:
![LaTeX \begin{displaymath}
T_1=\frac{(t-1)\left[\sum_{j=1}^tR_j^2-tC\right]}{A-C},
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img6263bdbeddade6aabd733985ed7a7916.png)
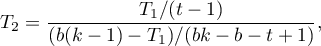
gdzie:
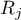 - suma rang dla kolejnych pomiarów
- suma rang dla kolejnych pomiarów 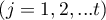 ,
,
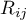 - rangi przypisane kolejnym pomiarom, oddzielnie dla każdego z badanych obiektów
- rangi przypisane kolejnym pomiarom, oddzielnie dla każdego z badanych obiektów 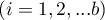 ,
,
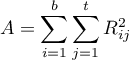
 suma kwadratów dla rang,
suma kwadratów dla rang,
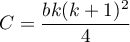
 współczynnik korekcji.
współczynnik korekcji.
Wzór na statystykę 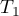 i
i 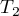 zawiera poprawkę na rangi wiązane.
zawiera poprawkę na rangi wiązane.
W przypadku danych kompletnych statystyka 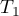 jest tożsama z testem Friedmana. Ma ona asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z
jest tożsama z testem Friedmana. Ma ona asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 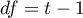 stopniami swobody.
stopniami swobody.
Statystyka 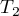 to odpowiednik korekty Iman-Davenport ANOVA Friedmana, więc podlega rozkładowi F Snedecora z
to odpowiednik korekty Iman-Davenport ANOVA Friedmana, więc podlega rozkładowi F Snedecora z 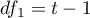 i
i  stopniami swobody. Uznaje się ją obecnie za bardziej precyzyjną niż statystykę
stopniami swobody. Uznaje się ją obecnie za bardziej precyzyjną niż statystykę 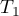 i rekomenduje jej stosowanie15).
i rekomenduje jej stosowanie15).
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC przeprowadzone zostało w rozdziale dotyczącym jednoczynnikowej analizy wariancji.
Stosowany dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
Hipotezy:
Przykład - porównania proste (porównanie pomiędzy sobą 2 wybranych median / sum rang):
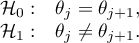
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
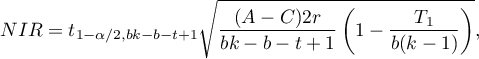
gdzie:
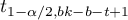 - to wartość krytyczna (statystyka) rozkładu t-Studenta dla poziomu istotności
- to wartość krytyczna (statystyka) rozkładu t-Studenta dla poziomu istotności  i
i 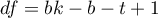 stopni swobody.
stopni swobody.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
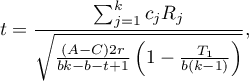
Statystyka ta podlega rozkładowi t-Studenta z 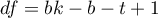 stopniami swobody.
stopniami swobody.
Okno z ustawieniami opcji ANOVA Durbina wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Friedmana (możliwość braków danych) lub poprzez Kreator.
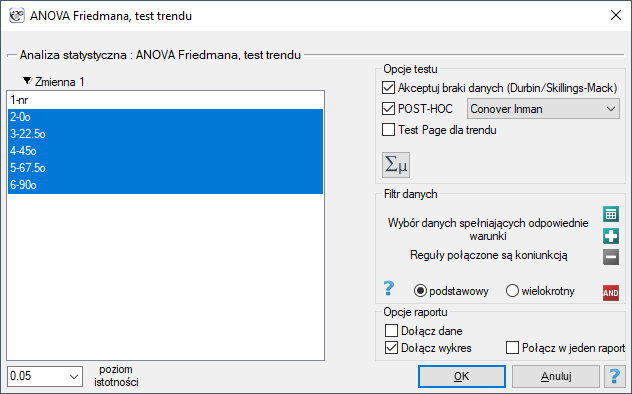
Uwaga!
By rekordy w których występują braki danych były brane pod uwagę wymagane jest zaznaczenie opcji Akceptuj braki danych. Jako braki danych traktowane są puste komórki oraz komórki o wartościach nieliczbowych. W analizie biorą udział tylko rekordy zawierające więcej niż jedną wartość liczbową.
Przeprowadzono eksperyment wśród 20 pacjentów szpitala psychiatrycznego (Ogilvie 1965 16)). Eksperyment ten polegał na odrysowaniu linii prostych według zaprezentowanego wzoru. Wzór przedstawiał 5 linii rysowanych pod różnym kątem (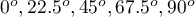 ) względem wskazanego środka. Zadaniem pacjentów było odwzorowanie linii mając zasłoniętą dłoń. Jako wynik eksperymentu zapisano czas w jakim pacjent kreślił daną linię. W idealnym przypadku każdy pacjent kreśliłby linię pod każdym kątem, jednak upływający czas i zmęczenie miałyby znaczny wpływ na wydajność pracy. Ponadto trudno jest utrzymać zainteresowanie pacjenta i chęć współpracy przez dłuższy czas. W związku z tym projekt zaplanowano i przeprowadzono w zbalansowanych i niekompletnych blokach. Każdy z 20 pacjentów wyrysowywał linię pod dwoma kontami (możliwych kątów było pięć). W ten sposób każdy kąt wyrysowywany był ośmiokrotnie. Czas w jakim każdy pacjent wyrysowywał linię pod zadanym kątem zapisano w tabeli.
) względem wskazanego środka. Zadaniem pacjentów było odwzorowanie linii mając zasłoniętą dłoń. Jako wynik eksperymentu zapisano czas w jakim pacjent kreślił daną linię. W idealnym przypadku każdy pacjent kreśliłby linię pod każdym kątem, jednak upływający czas i zmęczenie miałyby znaczny wpływ na wydajność pracy. Ponadto trudno jest utrzymać zainteresowanie pacjenta i chęć współpracy przez dłuższy czas. W związku z tym projekt zaplanowano i przeprowadzono w zbalansowanych i niekompletnych blokach. Każdy z 20 pacjentów wyrysowywał linię pod dwoma kontami (możliwych kątów było pięć). W ten sposób każdy kąt wyrysowywany był ośmiokrotnie. Czas w jakim każdy pacjent wyrysowywał linię pod zadanym kątem zapisano w tabeli.
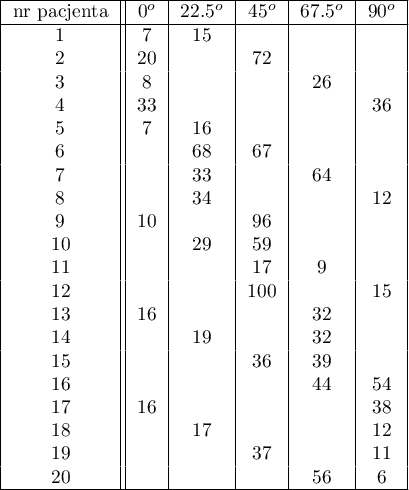
Chcemy sprawdzić, czy czas jaki został poświęcony na wyrysowanie poszczególnych linii jest zupełnie losowy, czy też są linie, których wyrysowywanie zajęło więcej lub mniej czasu.
Hipotezy:
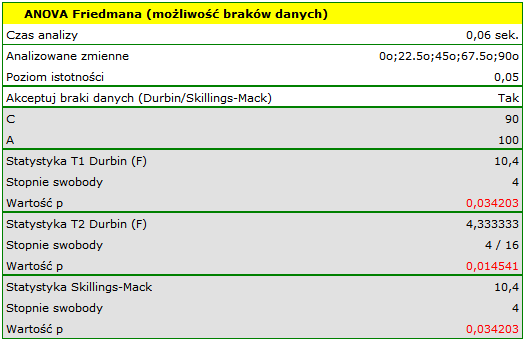
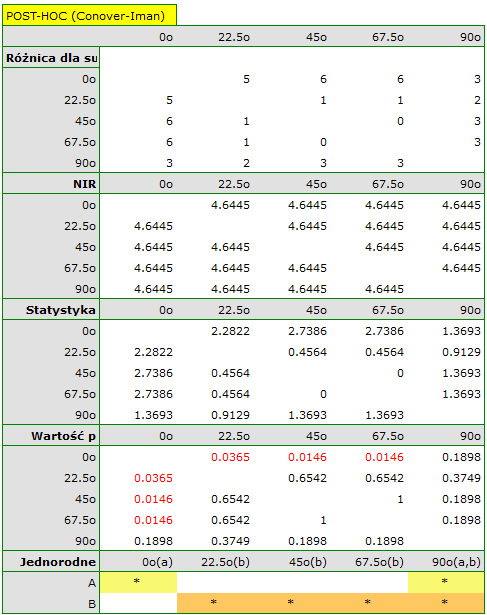
Porównując wartość 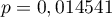 dla statystyki
dla statystyki 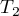 (lub wartość
(lub wartość 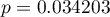 dla statystyki
dla statystyki 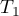 ) z poziomem istotności
) z poziomem istotności  stwierdzamy, że linie nie są rysowane w tym samym czasie. Wykonana analiza POST-HOC wskazuje na różnice czasu poświęconego na narysowanie linii pod kątem
stwierdzamy, że linie nie są rysowane w tym samym czasie. Wykonana analiza POST-HOC wskazuje na różnice czasu poświęconego na narysowanie linii pod kątem 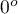 . Jest ona rysowana szybciej niż linie pod kątem
. Jest ona rysowana szybciej niż linie pod kątem 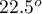 ,
, 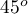 oraz
oraz 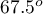 .
.
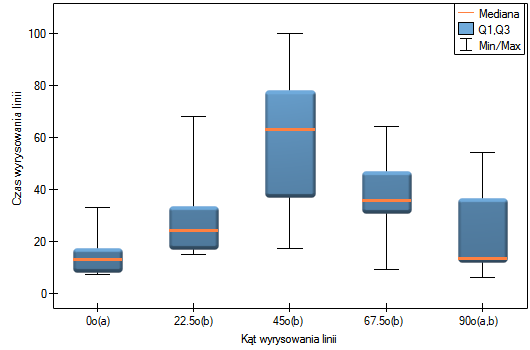
Na wykresie zaznaczono grupy jednorodne wskazane przez test post-hoc.
ANOVA Skillings-Mack (brakujących danych)
Analiza wariancji powtarzanych pomiarów dla rang Skillings-Mack została zaproponowana przez Skillings'a i Mack'a w roku 1981 17). Jest to test, który może być wykorzystywany w przypadku występowania braków danych, ale braki te nie muszą występować w żadnym szczególnym układzie. Każdy obiekt musi mieć jednak przynajmniej dwie obserwacje. Jeśli nie ma rang wiązanych a braki nie występują jest tożsamy z ANOVA Friedmana, a jeśli braki danych występują w układzie zbalansowanym odpowiada wynikom ANOVA Durbina.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości sumy rang dla kolejnych pomiarów (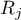 ) lub są upraszczane do median (
) lub są upraszczane do median (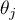 ):
):
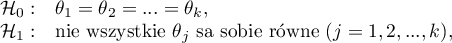
Statystyka testowa ma postać:
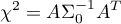
gdzie:
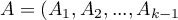
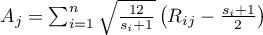 ,
,
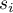 - liczba obserwacji dla
- liczba obserwacji dla  -tego obiektu,
-tego obiektu,
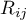 - rangi przypisane kolejnym pomiarom (
- rangi przypisane kolejnym pomiarom (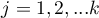 ), oddzielnie dla każdego z badanych obiektów (
), oddzielnie dla każdego z badanych obiektów (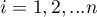 ), przy czym rangi dla braków danych równe są średniej randze dla danego obiektu,
), przy czym rangi dla braków danych równe są średniej randze dla danego obiektu,
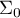 - macierz wyznaczająca kowariancje dla
- macierz wyznaczająca kowariancje dla  przy prawdziwości
przy prawdziwości  18).
18).
Gdy każda para pomiarów występuje równocześnie dla przynajmniej jednej obserwacji, statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 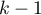 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji ANOVA Skillings-Mack wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Friedmana (możliwość braków danych) lub poprzez Kreator.
Uwaga!
By rekordy w których występują braki danych były brane pod uwagę wymagane jest zaznaczenie opcji Akceptuj braki danych. Jako braki danych traktowane są puste komórki oraz komórki o wartościach nieliczbowych. W analizie biorą udział tylko rekordy zawierające więcej niż jedną wartość liczbową.
Przykład (plik ankietyzacja.pqs)
Pewien nauczyciel akademicki, chcąc poprawić sposób prowadzenia zajęć postanowił zweryfikować swoje umiejętności dydaktyczne. W kilku losowo wybranych grupach studenckich, podczas ostatnich zajęć, prosił o wypełnienie krótkiej anonimowej ankiety. Ankieta składała się z 6 pytań dotyczących sposobu ilustrowania sześciu wyszczególnionych partii materiału. Studenci mogli dokonać oceny w skali pięciostopniowej , gdzie 1-zupełnie niezrozumiały sposób przedstawiana materiału, 5 - bardzo jasny i ciekawy sposób ilustrowania materiału. Uzyskane w ten sposób dane okazały się nie być kompletne ze względu na brak odpowiedzi studentów na pytania dotyczące tej części materiału, na której byli nieobecni. W 30-osobowej grupie wypełniającej ankietę, tylko 15 osób udzieliło kompletu odpowiedzi. Wykonanie analizy nie uwzględniającej braków danych (w tym przypadku analizy Friedmana) będzie miało ograniczoną moc poprzez tak drastyczne obcięcie liczności grupy i nie doprowadzi do wykrycia istotnych różnic. Braki danych nie były zaplanowane i nie występują w bloku zbalansowanym, a więc nie można wykonać tego zadania przy użyciu analizy Durbina wraz z jego testem POST-HOC.
Hipotezy:

Wyniki analizy ANOVA Skillings-Mack przedstawia następujący raport:
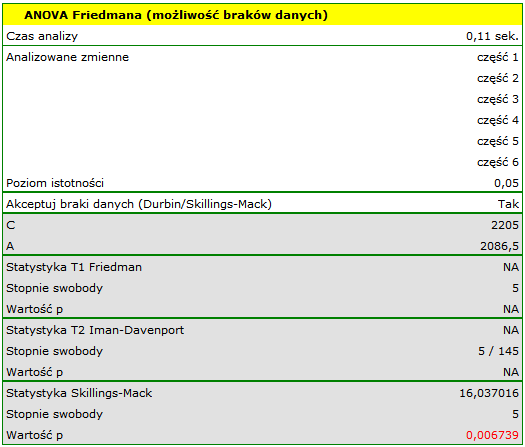
Uzyskaną wartość  należy traktować ostrożnie ze względu na możliwe rangi wiązane. Jednak w przypadku tego badania wartość
należy traktować ostrożnie ze względu na możliwe rangi wiązane. Jednak w przypadku tego badania wartość 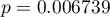 znajduje się znacznie poniżej przyjętego poziomu istotności
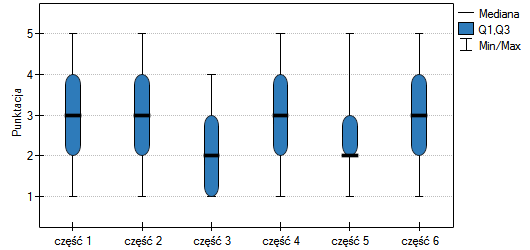
znajduje się znacznie poniżej przyjętego poziomu istotności  , co świadczy o występowaniu istotnych różnic. Różnice w odpowiedziach można obserwować na wykresie, nie ma jednak możliwości przeprowadzenia analizy POST-HOC dla tego testu.
, co świadczy o występowaniu istotnych różnic. Różnice w odpowiedziach można obserwować na wykresie, nie ma jednak możliwości przeprowadzenia analizy POST-HOC dla tego testu.
Test chi-kwadrat dla wielowymiarowych tabel kontyngencji
Test  dla wielowymiarowych tabel kontyngencji (ang. Chi-square test for multidimensional contingency tables) jest rozszerzeniem testu chi-kwadrat dla tabel (RxC) na więcej niż dwie cechy.
dla wielowymiarowych tabel kontyngencji (ang. Chi-square test for multidimensional contingency tables) jest rozszerzeniem testu chi-kwadrat dla tabel (RxC) na więcej niż dwie cechy.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę,
Hipotezy:
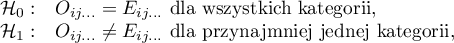
gdzie:
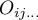 i
i 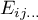 to liczności obserwowane w tabeli kontyngencji i odpowiadające im liczności oczekiwane.
to liczności obserwowane w tabeli kontyngencji i odpowiadające im liczności oczekiwane.
Statystyka testowa ma postać:
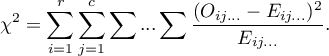
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru: 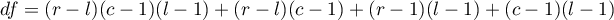 - dla tabeli o 3 wymiarach.
- dla tabeli o 3 wymiarach.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji wielowymiarowego testu chi-kwadrat wywołujemy poprzez menu Statystyka→Testy nieparametryczne→chi-kwadrat (wielowymiarowy) lub poprzez ''Kreator''.
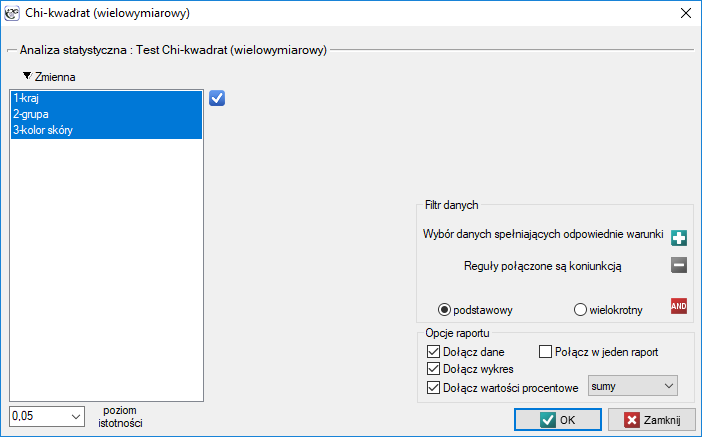
Uwaga!
Test ten jest możliwy do wyliczenia tylko na podstawie danych surowych.
ANOVA Q-Cochrana
Analiza wariancji Q-Cochrana oparta na teście Q-Cochrana (ang. Q-Cochran test) opisana została przez Cochrana (1950)20). Test ten jest rozszerzeniem testu McNemara do 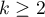 grup zależnych. Służy do weryfikacji hipotezy o symetryczności pomiędzy wynikami kilkukrotnych pomiarów
grup zależnych. Służy do weryfikacji hipotezy o symetryczności pomiędzy wynikami kilkukrotnych pomiarów 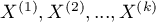 cechy
cechy  . Badana cecha może mieć tylko 2 wartości, do których (dla potrzeb analizy) przypisywane są liczby 0 i 1.
. Badana cecha może mieć tylko 2 wartości, do których (dla potrzeb analizy) przypisywane są liczby 0 i 1.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej (zmienne dychotomiczne, czyli zmienne o 2 kategoriach),
Hipotezy:
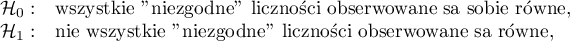
gdzie:
„niezgodne” liczności obserwowane, to liczności obserwowane wyliczone, gdy wartość badanej cechy jest różna w kolejnych pomiarach.
Statystyka testowa ma postać:
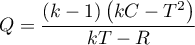
gdzie:
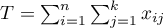 ,
,
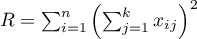 ,
,
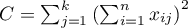 ,
,
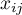
 wartość
wartość  -tego pomiaru dla
-tego pomiaru dla  -tego obiektu (czyli 0 lub 1).
-tego obiektu (czyli 0 lub 1).
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru: 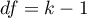 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC przeprowadzone zostało w rozdziale dotyczącym jednoczynnikowej analizy wariancji.
Stosowany dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
Hipotezy:
Przykład - porównania proste (dla różnicy proporcji 1 wybranej pary pomiarów):
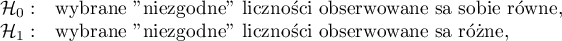
 Wartość najmniejszej istotnej różnicy wyliczana jest ze wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest ze wzoru:
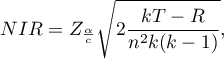
gdzie:
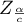 - to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności poziomu istotności
- to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności poziomu istotności  skorygowanego o liczbę możliwych porównań prostych
skorygowanego o liczbę możliwych porównań prostych  .
.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
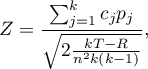
gdzie:
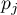
 proporcja
proporcja  -tego pomiaru
-tego pomiaru  ,
,
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład normalny, a wartość  jest korygowana o liczbę możliwych porównań prostych
jest korygowana o liczbę możliwych porównań prostych  .
.
Okno z ustawieniami opcji ANOVA Q Cochrana wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Q Cochrana lub poprzez ''Kreator''.
Uwaga!
Test ten jest możliwy do wyliczenia tylko na podstawie danych surowych.
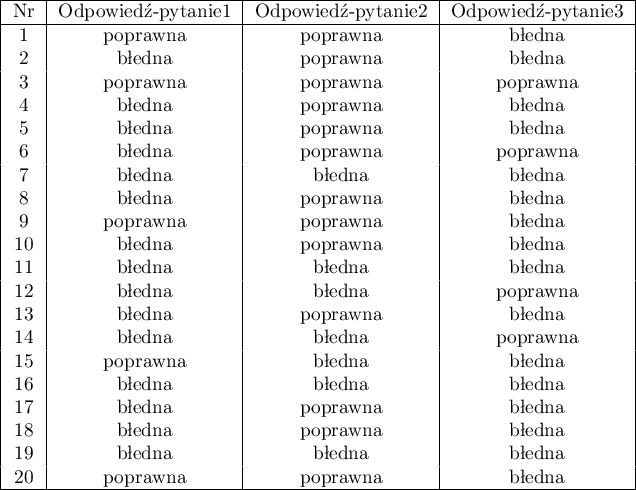
Chcemy porównać trudność 3 pytań testowych. W tym celu z badanej populacji osób, do których adresowany jest test wybieramy 20 osobową próbę. Każda osoba z próby daje odpowiedzi na 3 pytania zawarte w teście. Następnie sprawdzamy poprawność tych odpowiedzi (osoba może odpowiedzieć poprawnie lub błędnie). Wyniki zawiera poniższa tabela:
Hipotezy:

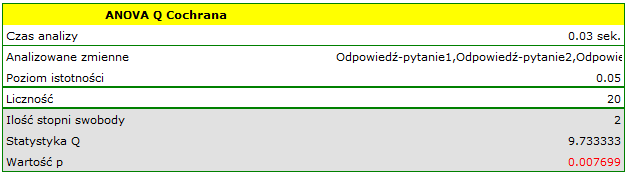
Porównując wartość 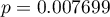 z poziomem istotności
z poziomem istotności  stwierdzamy, że pytanie testowe wykazują różny stopień trudności. Wznawiamy analizę przyciskiem
stwierdzamy, że pytanie testowe wykazują różny stopień trudności. Wznawiamy analizę przyciskiem  by wykonać test POST-HOC i w oknie opcji testu wybieramy POST-HOC
by wykonać test POST-HOC i w oknie opcji testu wybieramy POST-HOC Dunn.
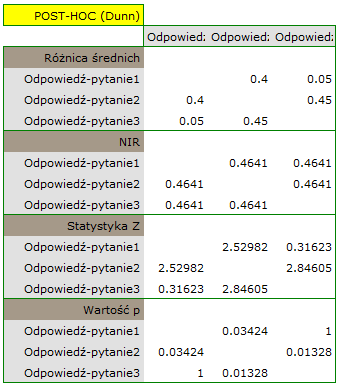
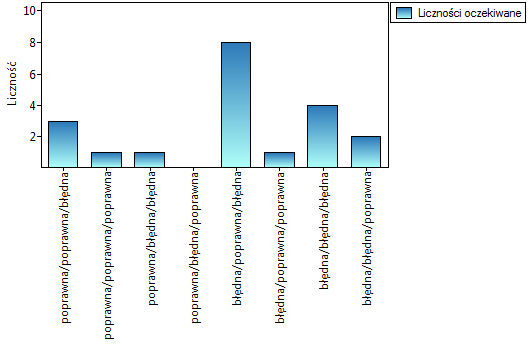
Wykonana analiza POST-HOC wskazuje, że różnice dotyczą pytania 2 i 1 oraz 2 i 3. Różnica ta polega na tym, że pytanie 2 jest łatwiejsze niż 1 i 3 (liczba poprawnych odpowiedzi jest tu wyższa).
