Spis treści
Korelacja
{\ovalnode{A}{\hyperlink{rozklad_normalny}{\begin{tabular}{c}Czy rozkład\\zmiennej jest\\rozkładem\\normalnym?\end{tabular}}}}
\rput[br](3.7,6.2){\rnode{B}{\psframebox{\hyperlink{wspolczynnik_pearsona}{\begin{tabular}{c}testy\\do sprawdzania\\istotności\\współczynnika\\korelacji liniowej $r_p$\\ lub równania regresji $\beta$\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{A}{B}
\rput(2.2,10.4){T}
\rput(4.3,12.5){N}
\rput(7.5,14){\hyperlink{porzadkowa}{Skala porządkowa}}
\rput[br](9.4,10.9){\rnode{C}{\psframebox{\hyperlink{wspolczynniki_monotoniczne}{\begin{tabular}{c}testy\\do sprawdzania\\istotności\\współczynnika\\korelacji monotonicznej\\$r_s$ lub $\tau$ \end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{A}{C}
\rput(12.5,14){\hyperlink{nominalna}{Skala nominalna}}
\rput[br](16,11.6){\rnode{D}{\psframebox{\hyperlink{wsp_tabel_kontyngencji}{\begin{tabular}{c}test $\chi^2$ i oparte na nim\\współczynniki kontyngencji: $C$, $\phi$, $V$\\lub test do sprawdzania istotności\\współczynnika kontyngencji $Q$\end{tabular}}}}}
\rput(6,9.8){\hyperlink{testy_normalnosci}{testy normalności}}
\rput(6,9.5){\hyperlink{testy_normalnosci}{rozkładu}}
\psline[linestyle=dotted]{<-}(3.4,11.2)(4,10)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imge2dd4664b43b4c34eb999fc85be62703.png)
Współczynniki korelacji są jedną z miar statystyki opisowej, która reprezentuje stopień korelacji (zależności) pomiędzy 2 lub więcej cechami (zmiennymi). Wybór konkretnego współczynnika zależy w głównej mierze od skali, na której dokonano pomiarów. Wyznaczenie go stanowi jeden z pierwszych etapów pracy nad analizą korelacji. Następnie istotność statystyczną otrzymanych współczynników można analizować przy pomocy testów statystycznych.
Uwaga!
Zależność pomiędzy zmiennymi nie zawsze obrazuje ich związek przyczynowo skutkowy.
Testy parametryczne
Współczynniki korelacji liniowej
Współczynnik korelacji liniowej Pearsona  (ang. Pearson product-moment correlation coefficient, Pearson (1896,1900)) jest wykorzystywany do badania siły związku liniowego pomiędzy cechami. Można go wyznaczać dla skali interwałowej, o ile brak jest odstających pomiarów, a rozkład reszt lub badanych cech jest rozkładem normalnym.
(ang. Pearson product-moment correlation coefficient, Pearson (1896,1900)) jest wykorzystywany do badania siły związku liniowego pomiędzy cechami. Można go wyznaczać dla skali interwałowej, o ile brak jest odstających pomiarów, a rozkład reszt lub badanych cech jest rozkładem normalnym.
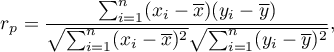
gdzie:
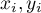 - kolejne wartości cechy
- kolejne wartości cechy  i
i  ,
,
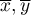 - średnie z wartości cechy
- średnie z wartości cechy  i cechy
i cechy  ,
,
 - liczność próby.
- liczność próby.
Uwaga!
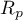 oznacza współczynnik korelacji Pearsona populacji, natomiast
oznacza współczynnik korelacji Pearsona populacji, natomiast 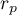 w próbie.
w próbie.
Wartość 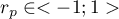 interpretujemy w następujący sposób:
interpretujemy w następujący sposób:
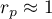 oznacza silną dodatnią zależność liniową, tj. punkty pomiarowe leżą blisko linii prostej a wzrostowi zmiennej niezależnej odpowiada wzrost zmiennej zależnej;
oznacza silną dodatnią zależność liniową, tj. punkty pomiarowe leżą blisko linii prostej a wzrostowi zmiennej niezależnej odpowiada wzrost zmiennej zależnej;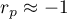 oznacza silną ujemną zależność liniową, tj. punkty pomiarowe leżą blisko linii prostej, lecz wzrostowi zmiennej niezależnej odpowiada spadek zmiennej zależnej;
oznacza silną ujemną zależność liniową, tj. punkty pomiarowe leżą blisko linii prostej, lecz wzrostowi zmiennej niezależnej odpowiada spadek zmiennej zależnej;- gdy współczynnik korelacji liniowej przyjmuje wartość równą lub bardzo bliską zeru wówczas nie istnieje liniowa zależność między badanymi parametrami (ale może istnieć związek nieliniowy).
Interpretacja graficzna współczynnika 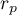 .
.
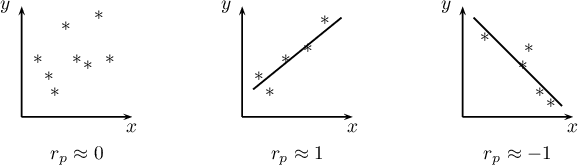
Gdy jedna z badanych cech jest stała (niezależnie od zmian drugiej cechy) to nie są one związane zależnością. Współczynnika 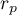 nie można wyznaczyć.
nie można wyznaczyć.
Uwaga!
Błędem jest wyznaczanie współczynnika korelacji, gdy w próbie występują obserwacje odstające, które mogą całkowicie przekłamać wartość i znak współczynnika korelacji Pearsona, gdy próba jest wyraźnie niejednorodna, bądź też badana zależność wyraźnie przyjmuje kształt inny niż liniowy.
Współczynnik determinacji - 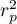 . Wyraża procent zmienności zmiennej zależnej tłumaczony zmiennością zmiennej niezależnej.
. Wyraża procent zmienności zmiennej zależnej tłumaczony zmiennością zmiennej niezależnej.
Tworzony model korelacji przedstawia zależność liniową postaci:
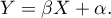
Współczynniki 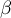 i
i  równania regresji liniowej możemy wyznaczyć z wzorów:
równania regresji liniowej możemy wyznaczyć z wzorów:
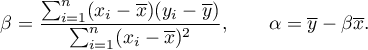
Przykład c.d. (plik wiek-wzrost.pqs)
Istotność współczynnika korelacji Pearsona
Test t do sprawdzania istotności współczynnika korelacji liniowej Pearsona
Test do sprawdzania istotności współczynnika korelacji liniowej Pearsona (ang. test of significance for a Pearson product-moment correlation coefficient) służy do weryfikacji hipotezy o braku zależności liniowej pomiędzy badanymi cechami populacji i opiera się na współczynniku korelacji liniowej Pearsona wyliczonym dla próby. Im wartość współczynnika 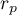 jest bliższa 0, tym słabszą zależnością związane są badane cechy.
jest bliższa 0, tym słabszą zależnością związane są badane cechy.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu badanych cech w populacji lub normalność reszt modelu.
Hipotezy:
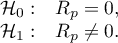
Statystyka testowa ma postać:
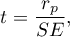
gdzie 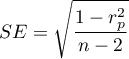 .
.
Wartość statystyki testowej nie może być wyznaczona, gdy 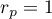 lub
lub 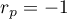 albo, gdy
albo, gdy 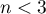 .
.
Statystyka testowa ma rozkład t-Studenta z 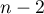 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Przykład c.d. (plik wiek-wzrost.pqs)
Istotność współczynnika nachylenia prostej
Test t do sprawdzania istotności współczynników równania regresji liniowej
Test ten służy do weryfikacji hipotezy o braku zależności liniowej pomiędzy badanymi cechami populacji i opiera się na współczynniku nachylenia prostej wyliczonym dla próby. Im wartość współczynnika 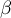 będzie bliższa 0, tym słabszą zależność dopasowana prosta przedstawia.
będzie bliższa 0, tym słabszą zależność dopasowana prosta przedstawia.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu badanych cech w populacji lub normalność reszt modelu.
Hipotezy:
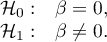
Statystyka testowa ma postać:
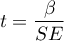
gdzie:
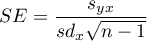 ,
,
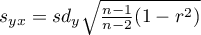 ,
,
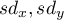 - odchylenie standardowe wartości cechy
- odchylenie standardowe wartości cechy  i cechy
i cechy  .
.
Wartość statystyki testowej nie może być wyznaczona, gdy 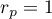 lub
lub 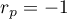 albo, gdy
albo, gdy 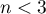 .
.
Statystyka testowa ma rozkład t-Studenta z 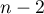 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Predykcja
polega na przewidywaniu wartości jednej ze zmiennych (najczęściej zmiennej zależnej 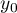 ) na podstawie wartości innej zmiennej (najczęściej zmiennej niezależnej
) na podstawie wartości innej zmiennej (najczęściej zmiennej niezależnej 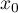 ). Dokładność wyznaczonej wartości określają obliczone dla niej przedziały predykcji.
). Dokładność wyznaczonej wartości określają obliczone dla niej przedziały predykcji.
- Interpolacja polega na przewidywaniu wartości zadanej zmiennej leżącej wewnątrz obszaru, dla którego wykonaliśmy model regresji. Interpolacja jest więc z reguły procedurą bezpieczną - zakłada się tu jedynie ciągłość funkcji wyrażającej zależność obu zmiennych.
- Ekstrapolacja polega na przewidywaniu wartości zadanej zmiennej leżącej poza obszarem, dla którego zbudowaliśmy model regresji. W przeciwieństwie do interpolacji, ekstrapolacja bywa często zabiegiem ryzykownym i dokonuje się jej jedynie w niewielkiej odległości od obszaru, dla którego powstał model regresji. Podobnie jak w interpolacji zakłada się ciągłość funkcji wyrażającej zależność obu zmiennych.
Analiza reszt modelu - wyjaśnienie w module Regresja Wieloraka.
Okno z ustawieniami opcji zależności liniowej Pearsona wywołujemy poprzez menu Statystyka→Testy parametryczne→zależność liniowa (r-Pearsona) lub poprzez ''Kreator''.
Przykład (plik wiek-wzrost.pqs)
Wśród uczniów pewnej szkoły baletowej badano zależność pomiędzy wiekiem a wzrostem. W tym celu pobrano próbę obejmującą szesnaścioro dzieci i zapisano dla nich następujące wyniki pomiaru tych cech:
(wiek, wzrost): (5, 128) (5, 129) (5, 135) (6, 132) (6, 137) (6, 140) (7, 148) (7, 150) (8, 135) (8, 142) (8, 151) (9, 138) (9, 153) (10, 159) (10, 160) (10, 162).}
Hipotezy:

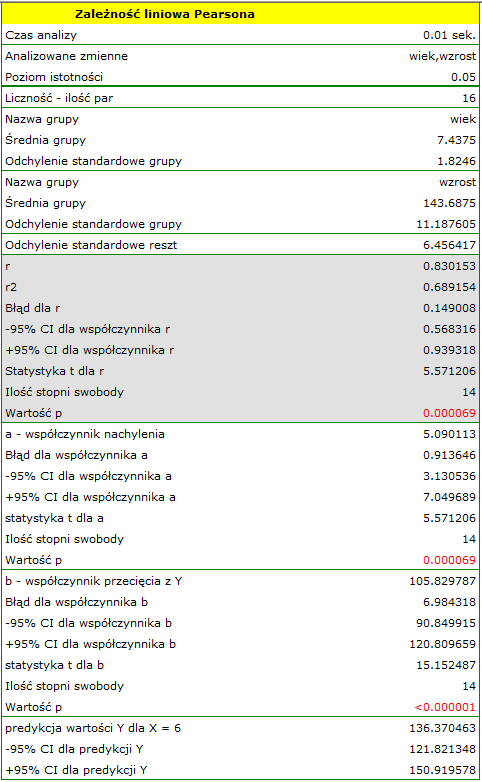
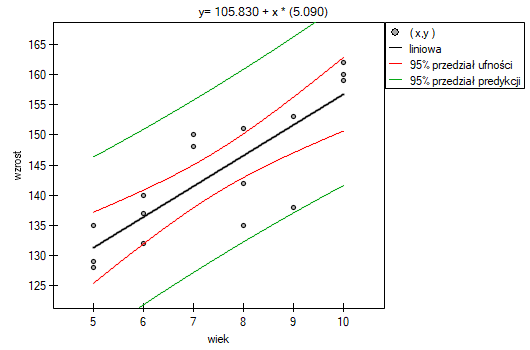
Porównując wartość  =0.000069 z poziomem istotności
=0.000069 z poziomem istotności  stwierdzamy, że istnieje zależność liniowa pomiędzy wiekiem a wzrostem dla populacji dzieci badanej szkoły. Zależność ta jest wprost proporcjonalna, tzn. wraz ze wzrostem wieku dzieci rośnie wysokość ciała.
stwierdzamy, że istnieje zależność liniowa pomiędzy wiekiem a wzrostem dla populacji dzieci badanej szkoły. Zależność ta jest wprost proporcjonalna, tzn. wraz ze wzrostem wieku dzieci rośnie wysokość ciała.
Współczynnik korelacji liniowej Pearsona, a zatem siła związku liniowego pomiędzy wiekiem a wzrostem wynosi 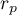 =0.8302. Współczynnik determinacji
=0.8302. Współczynnik determinacji 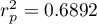 oznacza, że ok. 69% zmienności wzrostu jest tłumaczona zmiennością wieku.
oznacza, że ok. 69% zmienności wzrostu jest tłumaczona zmiennością wieku.
Z równania regresji postaci:
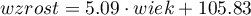 można wyliczyć predykcyjną wartość dla dziecka w wieku np. 6 lat. Przewidywany wzrost takiego dziecka wynosi 136.37cm.
można wyliczyć predykcyjną wartość dla dziecka w wieku np. 6 lat. Przewidywany wzrost takiego dziecka wynosi 136.37cm.
Porównanie współczynników korelacji
Test t do sprawdzania równości współczynników korelacji liniowej Pearsona pochodzących z 2 niezależnych populacji
Test ten służy do weryfikacji hipotezy o równości dwóch współczynników korelacji liniowej Pearsona (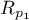 ,
, 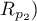 .
.
Podstawowe warunki stosowania:
- współczynniki
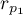 i
i 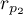 badają zależność tych samych cech
badają zależność tych samych cech  i
i  ,
, - znane są liczności obu prób
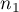 i
i 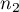 .
.
Hipotezy:
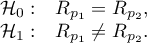
Statystyka testowa ma postać:
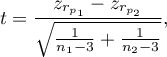
gdzie:
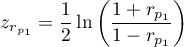 ,
,
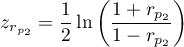 .
.
Statystyka testowa ma rozkład t-Studenta z 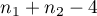 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga! W podobny sposób można dokonać porównania współczynników nachylenia prostych regresji.
Porównanie nachylenia prostych regresji
Test t do sprawdzania równości współczynników regresji liniowej pochodzących z 2 niezależnych populacji
Test ten służy do weryfikacji hipotezy o równości dwóch współczynników regresji liniowej 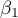 i
i 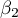 w badanych populacjach.
w badanych populacjach.
Podstawowe warunki stosowania:
- współczynniki
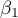 i
i 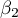 badają zależność tych samych cech
badają zależność tych samych cech  i
i  ,
, - znane są liczności obu prób
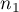 i
i 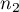 ,
,
Hipotezy:
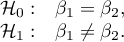
Statystyka testowa ma postać:
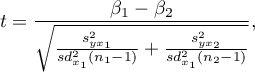
gdzie:
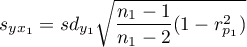 ,
,
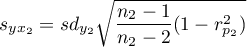 .
.
Statystyka testowa ma rozkład t-Studenta z 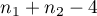 stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji porównania współczynników zależności wywołujemy poprzez menu Statystyka→Testy parametryczne→porównanie współczynników zależności.
Testy nieparametryczne
Współczynniki korelacji monotonicznej
Zależność monotoniczna może być opisywana jako monotoniczny wzrost lub monotoniczny spadek. Związek pomiędzy 2 cechami przedstawia monotoniczny wzrost jeżeli wzrostowi jednej cechy towarzyszy wzrost drugiej cechy. Związek pomiędzy 2 cechami przedstawia monotoniczny spadek jeżeli wzrostowi jednej cechy towarzyszy spadek drugiej cechy.
Współczynnik korelacji rangowej Spearmana 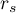 (ang. Spearman's rank-order correlation coefficient) jest wykorzystywany do badania siły związku monotonicznego pomiędzy cechami
(ang. Spearman's rank-order correlation coefficient) jest wykorzystywany do badania siły związku monotonicznego pomiędzy cechami  i
i  . Wyznacza się go dla skali porządkowej lub interwałowej.
. Wyznacza się go dla skali porządkowej lub interwałowej.
Wartość współczynnika korelacji rangowej Spearmana wylicza się według wzoru:
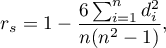
Wzór ten ulega pewniej modyfikacji gdy występują rangi wiązane:
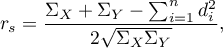
gdzie:
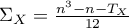 ,
, 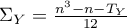 ,
,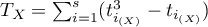 ,
, 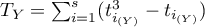 ,
, - liczba przypadków wchodzących w skład rangi wiązanej.
- liczba przypadków wchodzących w skład rangi wiązanej.
Poprawka na rangi wiązane powinna być stosowana, gdy rangi wiązane występują. Gdy nie ma rang wiązanych poprawka redukuje się i sprowadza wzór do postaci opisanej wcześniejszym równaniem.
Uwaga!
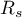 oznacza współczynnik korelacji rangowej Spearmana populacji, natomiast
oznacza współczynnik korelacji rangowej Spearmana populacji, natomiast 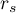 w próbie.
w próbie.
Wartość 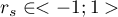 interpretujemy w następujący sposób:
interpretujemy w następujący sposób:
 oznacza silną dodatnią zależność monotoniczną (rosnącą), tj. wzrostowi zmiennej niezależnej odpowiada wzrost zmiennej zależnej;
oznacza silną dodatnią zależność monotoniczną (rosnącą), tj. wzrostowi zmiennej niezależnej odpowiada wzrost zmiennej zależnej;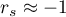 oznacza silną ujemną zależność monotoniczną (malejącą), tj. wzrostowi zmiennej niezależnej odpowiada spadek zmiennej zależnej;
oznacza silną ujemną zależność monotoniczną (malejącą), tj. wzrostowi zmiennej niezależnej odpowiada spadek zmiennej zależnej;- gdy współczynnik korelacji rangowej Spearmana przyjmuje wartość równą lub bardzo bliską zeru, wówczas nie istnieje monotoniczna zależność między badanymi parametrami (ale może istnieć związek niemonotoniczny np. sinusoidalny).
Współczynnik korelacji tau Kendalla  (ang. Kendall's tau correlation coefficient, Kendall (1938)1)) jest wykorzystywany do badania siły związku monotonicznego pomiędzy cechami. Wyznacza się go dla skali porządkowej lub interwałowej.
(ang. Kendall's tau correlation coefficient, Kendall (1938)1)) jest wykorzystywany do badania siły związku monotonicznego pomiędzy cechami. Wyznacza się go dla skali porządkowej lub interwałowej.
Wartość współczynnika korelacji tau Kendalla  wylicza się według wzoru:
wylicza się według wzoru:
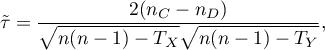
gdzie:
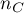 - liczbapar obserwacji, dla których wartości rang dla cechy
- liczbapar obserwacji, dla których wartości rang dla cechy  jak i dla cechy
jak i dla cechy  zmieniają się w tym samym kierunku (liczba par zgodnych),
zmieniają się w tym samym kierunku (liczba par zgodnych),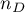 - liczba par obserwacji, dla których wartości rang dla cechy
- liczba par obserwacji, dla których wartości rang dla cechy  zmieniają się w innym kierunku niż dla cechy
zmieniają się w innym kierunku niż dla cechy  (liczba par niezgodnych),
(liczba par niezgodnych),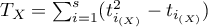 ,
, 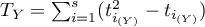 ,
, - liczba przypadków wchodzących w skład rangi wiązanej.
- liczba przypadków wchodzących w skład rangi wiązanej.
Wzór na współczynnik  zawiera poprawkę na rangi wiązane. Poprawka ta powinna być stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka nie jest wyliczana gdyż wówczas
zawiera poprawkę na rangi wiązane. Poprawka ta powinna być stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka nie jest wyliczana gdyż wówczas 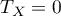 i
i 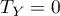 ) .
) .
Uwaga!
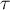 oznacza współczynnik korelacji Kendalla w populacji, natomiast
oznacza współczynnik korelacji Kendalla w populacji, natomiast  w próbie.
w próbie.
Wartość  interpretujemy w następujący sposób:
interpretujemy w następujący sposób:
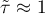 oznacza silną „zgodność” uporządkowania rang (zależność monotoniczną rosnącą), tj. wzrostowi zmiennej niezależnej odpowiada wzrost zmiennej zależnej;
oznacza silną „zgodność” uporządkowania rang (zależność monotoniczną rosnącą), tj. wzrostowi zmiennej niezależnej odpowiada wzrost zmiennej zależnej;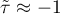 oznacza silną „niezgodność” uporządkowania rang (zależność monotoniczną malejącą), tj. wzrostowi zmiennej niezależnej odpowiada spadek zmiennej zależnej;
oznacza silną „niezgodność” uporządkowania rang (zależność monotoniczną malejącą), tj. wzrostowi zmiennej niezależnej odpowiada spadek zmiennej zależnej;- gdy współczynnik korelacji
 przyjmuje wartość równą lub bardzo bliską zeru wówczas nie istnieje monotoniczna zależność między badanymi parametrami (ale może istnieć związek niemonotoniczny np. sinusoidalny).
przyjmuje wartość równą lub bardzo bliską zeru wówczas nie istnieje monotoniczna zależność między badanymi parametrami (ale może istnieć związek niemonotoniczny np. sinusoidalny).
Współczynnik 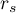 Spearmana a współczynnik
Spearmana a współczynnik  Kendalla
Kendalla
- dla skali interwałowej z normalnością rozkładu obu cech wartość
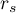 daje rezultaty bliższe wartości
daje rezultaty bliższe wartości 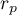 natomiast wartości
natomiast wartości  może znacznie różnić się od
może znacznie różnić się od 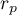 ,
, - wartość
 jest mniejsza bądź równa wartości
jest mniejsza bądź równa wartości 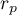 ,
,  jest nieobciążonym estymatorem parametru populacji
jest nieobciążonym estymatorem parametru populacji 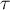 , podczas gdy wartość
, podczas gdy wartość 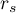 nie jest estymatorem nieobciążonym parametru
nie jest estymatorem nieobciążonym parametru 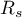 .
.
Przykład c.d. (plik wiek-wzrost.pqs)
Istotność współczynnika korelacji Spearmana
Test t do sprawdzania istotności współczynnika korelacji rangowej Spearmana (ang. Test of significance for Spearman's rank-order correlation coefficient) służy do weryfikacji hipotezy o braku zależności monotonicznej pomiędzy badanymi cechami populacji i opiera się na współczynniku korelacji rangowej Spearmana wyliczonym dla próby. Im wartość współczynnika Spearmana (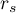 ) jest bliższa 0, tym słabszą zależnością monotoniczną związane są badane cechy.
) jest bliższa 0, tym słabszą zależnością monotoniczną związane są badane cechy.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej.
Hipotezy:
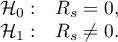
Statystyka testowa ma postać:
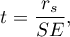 gdzie
gdzie 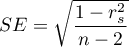 .
.
Wartość statystyki testowej nie może być wyznaczona gdy 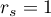 lub
lub 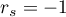 albo, gdy
albo, gdy 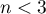 .
.
Statystyka testowa ma rozkład t-Studenta z 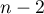 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji zależności monotonicznej Spearmana wywołujemy poprzez menu Statystyka→Testy nieparametryczne→zależność monotoniczna (r-Spearmana) lub poprzez ''Kreator''.
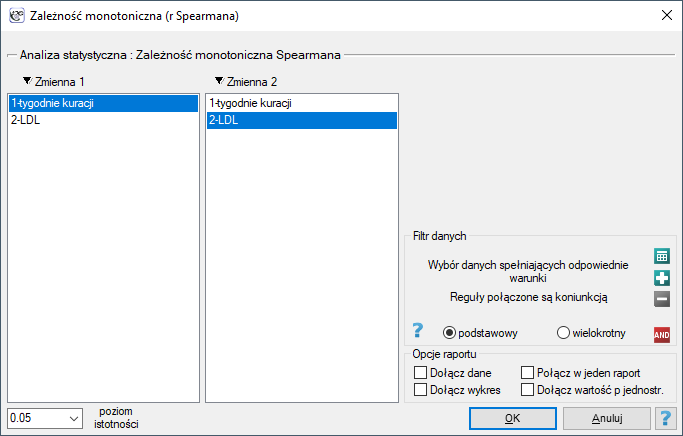
Przykład (plik: LDL tygodnie.pqs)
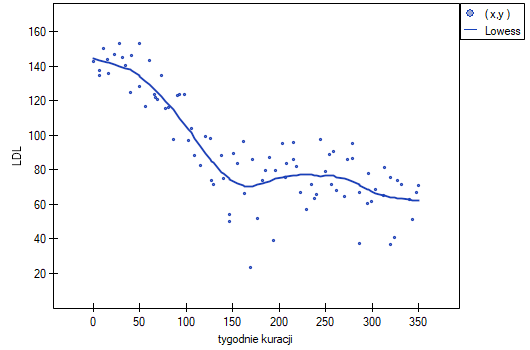
Badano skuteczność nowej terapii, której celem jest obniżenie poziomu cholesterolu we frakcji LDL. Przebadano 88 osób na różnym etapie kuracji. Sprawdzimy, czy wraz z upływem czasu stosowania kuracji (czas w tygodniach) poziom cholesterolu LDL spada i się stabilizuje.
Hipotezy:


Porównując wartość  <0.0001 z poziomem istotności
<0.0001 z poziomem istotności  stwierdzamy, że istnieje ważna statystycznie monotoniczna zależność pomiędzy czasem kuracji a poziomem LDL. Zależność ta jest początkowo malejąca, a po 150 tygodniach zaczyna się stabilizować. Współczynnik korelacji monotonicznej Spearmana, a zatem siła związku monotonicznego dla tej zależności jest dość wysoki i wynosi
stwierdzamy, że istnieje ważna statystycznie monotoniczna zależność pomiędzy czasem kuracji a poziomem LDL. Zależność ta jest początkowo malejąca, a po 150 tygodniach zaczyna się stabilizować. Współczynnik korelacji monotonicznej Spearmana, a zatem siła związku monotonicznego dla tej zależności jest dość wysoki i wynosi 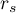 =-0.7806. Wykres wyrysowano dopasowując krzywą poprzez lokalne techniki wygładzania liniowego typu LOWESS.
=-0.7806. Wykres wyrysowano dopasowując krzywą poprzez lokalne techniki wygładzania liniowego typu LOWESS.
Istotność współczynnika korelacji tau Kendalla
Test do sprawdzania istotności współczynnika korelacji tau Kendalla
Test do sprawdzania istotności współczynnika korelacji  Kendalla (ang. Test of significance for Kendall's tau correlation coefficient) służy do weryfikacji hipotezy o braku zależności monotonicznej pomiędzy badanymi cechami populacji i opiera się na współczynniku korelacji Kendalla wyliczonym dla próby. Im wartość wspołczynnika tau (
Kendalla (ang. Test of significance for Kendall's tau correlation coefficient) służy do weryfikacji hipotezy o braku zależności monotonicznej pomiędzy badanymi cechami populacji i opiera się na współczynniku korelacji Kendalla wyliczonym dla próby. Im wartość wspołczynnika tau ( ) jest bliższa 0, tym słabszą zależnością monotoniczną związane są badane cechy.
) jest bliższa 0, tym słabszą zależnością monotoniczną związane są badane cechy.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej.
Hipotezy:
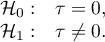
Statystyka testowa ma postać:
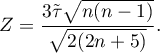 Statystyka testowa ma asymptotycznie (dla dużych liczności) rozkład normalny.
Statystyka testowa ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji zależności monotonicznej Kendalla wywołujemy poprzez menu Statystyka→Testy nieparametryczne→zależność monotoniczna (tau-Kendalla) lub poprzez ''Kreator''.
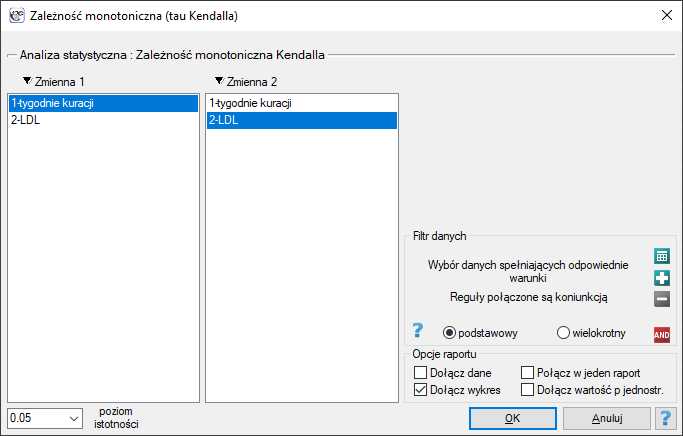
Przykład c.d. (plik LDL tygodnie.pqs)
Hipotezy:

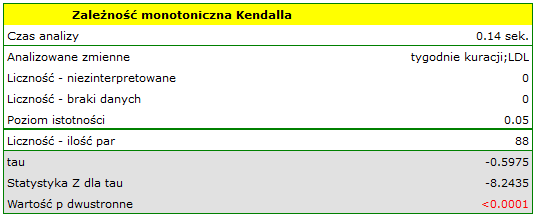
Porównując wartość  <0.0001 z poziomem istotności
<0.0001 z poziomem istotności  stwierdzamy, że istnieje ważna statystycznie monotoniczna zależność pomiędzy czasem kuracji a poziomem LDL. Zależność ta jest początkowo malejąca, a po 150 tygodniach zaczyna się stabilizować. Współczynnik korelacji monotonicznej Kendalla, a zatem siła związku monotonicznego dla tej zależności jest dość wysoki i wynosi
stwierdzamy, że istnieje ważna statystycznie monotoniczna zależność pomiędzy czasem kuracji a poziomem LDL. Zależność ta jest początkowo malejąca, a po 150 tygodniach zaczyna się stabilizować. Współczynnik korelacji monotonicznej Kendalla, a zatem siła związku monotonicznego dla tej zależności jest dość wysoki i wynosi  =-0.5975. Wykres wyrysowano dopasowując krzywą poprzez lokalne techniki wygładzania liniowego typu LOWESS.
=-0.5975. Wykres wyrysowano dopasowując krzywą poprzez lokalne techniki wygładzania liniowego typu LOWESS.

Współczynniki tabel kontyngencji i ich istotność statystyczna
Współczynniki kontyngencji są wyliczane dla danych w postaci surowej lub danych zebranych w tabelę kontyngencji.
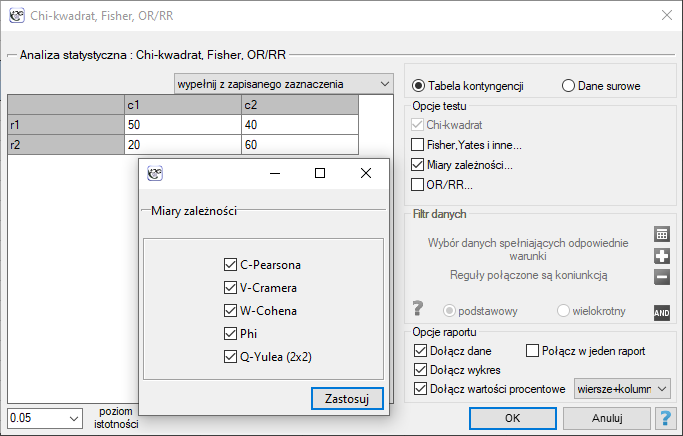
Okno z ustawieniami opcji miar zależności dla tabel wywołujemy poprzez menu Statystyka→Testy nieparametryczne →Chi-kwadrat, Fisher, OR/RR→Współczynniki korelacji… lub poprzez ''Kreator''.
Współczynnik kontyngencji Q-Yulea
Współczynnik kontyngencji  -Yulea (Yule's Q contingency coefficient), Yule (1900)2), jest miarą zależności, która może być wyznaczana dla tabel kontyngencji
-Yulea (Yule's Q contingency coefficient), Yule (1900)2), jest miarą zależności, która może być wyznaczana dla tabel kontyngencji 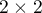
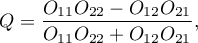
gdzie:
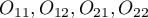 - liczności obserwowane w tabeli kontyngencji.
- liczności obserwowane w tabeli kontyngencji.
Oryginalnie wartość współczynnika  mieści się w przedziale
mieści się w przedziale 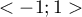 . Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa
. Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa  1 lub +1, tym siła badanego związku jest większa (ze względu na błędy w interpretacji ujemnej wartości współczynnika, wyniki tego współczynnika w programie PQStat przedstawiane są wówczas również jako wartość bezwzględna). Wadą tego współczynnika jest to, iż jest mało odporny na małe liczności obserwowane (gdy jakaś z liczności obserwowanych wynosi 0, to współczynnik może błędnie wskazywać całkowitą zależność cech).
1 lub +1, tym siła badanego związku jest większa (ze względu na błędy w interpretacji ujemnej wartości współczynnika, wyniki tego współczynnika w programie PQStat przedstawiane są wówczas również jako wartość bezwzględna). Wadą tego współczynnika jest to, iż jest mało odporny na małe liczności obserwowane (gdy jakaś z liczności obserwowanych wynosi 0, to współczynnik może błędnie wskazywać całkowitą zależność cech).
Istotność statystyczną wyznaczonego współczynnika kontyngencji  -Yulea określamy testem
-Yulea określamy testem  .
.
Hipotezy:
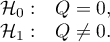
Statystyka testowa ma postać:
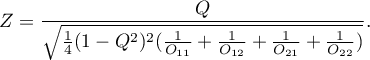
Statystyka testowa ma asymptotycznie (dla dużych liczności  ) rozkład normalny.
) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Współczynnik kontyngencji 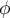 (ang. phi contingency coefficient) jest miarą zależności polecaną szczególnie dla tabel kontyngencji
(ang. phi contingency coefficient) jest miarą zależności polecaną szczególnie dla tabel kontyngencji 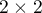 , chociaż możliwą do wyznaczenia dla dowolnych tabel.
, chociaż możliwą do wyznaczenia dla dowolnych tabel.
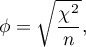
Wartość współczynnika 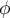 mieści się w przedziale
mieści się w przedziale 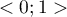 . Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa wartości 1 tym większa.
. Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa wartości 1 tym większa.
Współczynnik kontyngencji 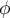 uznaje się za istotny statystycznie jeśli wartość
uznaje się za istotny statystycznie jeśli wartość  wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności
wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności  .
.
Współczynnik kontyngencji 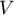 -Cramera
-Cramera
Współczynnik kontyngencji 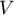 -Cramera (ang. Cramer's V contingency coefficient), Cramer (1946)3), jest rozszerzeniem współczynnika
-Cramera (ang. Cramer's V contingency coefficient), Cramer (1946)3), jest rozszerzeniem współczynnika 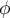 na tabele kontyngencji
na tabele kontyngencji 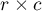 .
.
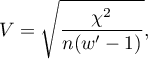
gdzie:
wartość - wartość statystyki testu chi-kwadrat,
- wartość statystyki testu chi-kwadrat,
 - całkowita liczność w tabeli kontyngencji,
- całkowita liczność w tabeli kontyngencji,
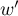 - jest mniejszą z dwóch wartości
- jest mniejszą z dwóch wartości  i
i  .
.
Wartość współczynnika 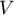 mieści się w przedziale
mieści się w przedziale 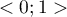 . Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa +1, tym siła badanego związku jest większa. Wartość współczynnika
. Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa +1, tym siła badanego związku jest większa. Wartość współczynnika 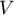 zależy również od wielkości tabeli, stąd nie powinno się stosować tego współczynnika do porównywania tabel kontyngencji o różnych wielkościach.
zależy również od wielkości tabeli, stąd nie powinno się stosować tego współczynnika do porównywania tabel kontyngencji o różnych wielkościach.
Współczynnik kontyngencji 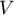 uznaje się za istotny statystycznie jeśli wartość
uznaje się za istotny statystycznie jeśli wartość  wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności
wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności  .
.
Współczynnik kontyngencji  -Cohena
-Cohena
Współczynnik kontyngencji  -Cohena (ang. Cohen's w contingency coefficient), Cohen (1988)4), jest modyfikacją współczynnika
-Cohena (ang. Cohen's w contingency coefficient), Cohen (1988)4), jest modyfikacją współczynnika 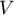 -Cramera i jest możliwy do wyliczenia dla tabel
-Cramera i jest możliwy do wyliczenia dla tabel 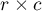 .
.
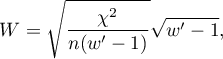
gdzie:
wartość - wartość statystyki testu chi-kwadrat,
- wartość statystyki testu chi-kwadrat,
 - całkowita liczność w tabeli kontyngencji,
- całkowita liczność w tabeli kontyngencji,
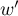 - jest mniejszą z dwóch wartości
- jest mniejszą z dwóch wartości  i
i  .
.
Wartość współczynnika  mieści się w przedziale
mieści się w przedziale 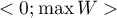 , gdzie
, gdzie  (dla tabel, w których co najmniej jedna zmienna zawiera tylko dwie kategorie wartość współczynnika
(dla tabel, w których co najmniej jedna zmienna zawiera tylko dwie kategorie wartość współczynnika  mieści się w przedziale
mieści się w przedziale 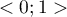 ). Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa maksymalnej wartości, tym siła badanego związku jest większa. Wartość współczynnika
). Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im bliższa maksymalnej wartości, tym siła badanego związku jest większa. Wartość współczynnika  zależy od wielkości tabeli, stąd nie powinno się stosować tego współczynnika do porównywania tabel kontyngencji o różnych wielkościach.
zależy od wielkości tabeli, stąd nie powinno się stosować tego współczynnika do porównywania tabel kontyngencji o różnych wielkościach.
Współczynnik kontyngencji  uznaje się za istotny statystycznie jeśli wartość
uznaje się za istotny statystycznie jeśli wartość  wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności
wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności  .
.
Współczynnik kontyngencji C Pearsona
Współczynnik kontyngencji  -Pearsona (ang. Pearson's C contingency coefficient) jest miarą zależności wyznaczaną dla tabel kontyngencji
-Pearsona (ang. Pearson's C contingency coefficient) jest miarą zależności wyznaczaną dla tabel kontyngencji 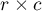
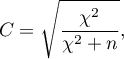
Wartość współczynnika  mieści się w przedziale
mieści się w przedziale 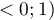 . Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im dalsza od 0, tym siła badanego związku jest większa. Ponieważ wartość współczynnika
. Im wartość ta jest bliższa 0, tym siła związku pomiędzy badanymi cechami jest mniejsza, a im dalsza od 0, tym siła badanego związku jest większa. Ponieważ wartość współczynnika  zależy również od wielkości tabeli (im większa tabela, tym wartość
zależy również od wielkości tabeli (im większa tabela, tym wartość  może być bliższa 1), dlatego wyznacza się górną granicę jaką dla danej wielkości tabeli współczynnik
może być bliższa 1), dlatego wyznacza się górną granicę jaką dla danej wielkości tabeli współczynnik  może osiągnąć:
może osiągnąć:
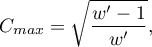
gdzie:
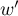 - jest mniejszą z dwóch wartości
- jest mniejszą z dwóch wartości  i
i  .
.
Niewygodną konsekwencją uzależnienia wartości  od wielkości tabeli jest brak możliwości porównywania wartości współczynnika
od wielkości tabeli jest brak możliwości porównywania wartości współczynnika  wyznaczonego dla różnych wielkości tabel kontyngencji. Nieco lepszą miarą w takim przypadku jest dostosowana do wielkości tabeli wielkość współczynnika kontyngencji
wyznaczonego dla różnych wielkości tabel kontyngencji. Nieco lepszą miarą w takim przypadku jest dostosowana do wielkości tabeli wielkość współczynnika kontyngencji 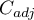
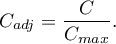
Współczynnik kontyngencji  uznaje się za istotny statystycznie jeśli wartość
uznaje się za istotny statystycznie jeśli wartość  wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności
wyznaczona na podstawie statystyki testu chi-kwadrat i rozkładu chi-kwadrat (wyznaczonego dla tej tabeli) jest równa bądź mniejsza niż poziom istotności  .
.
Przykład (plik płeć-egzamin.pqs)
Rozpatrzmy próbę składającą się z 170 osób (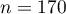 ), dla których badamy 2 cechy (
), dla których badamy 2 cechy ( =płeć,
=płeć,  =zdawalność egzaminu). Każda z tych cech występuje w dwóch kategoriach (
=zdawalność egzaminu). Każda z tych cech występuje w dwóch kategoriach ( =k,
=k,  =m,
=m, 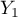 =tak,
=tak, 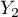 =nie). Na podstawie tej próby chcielibyśmy się dowiedzieć, czy w badanej populacji istnieje zależność pomiędzy płcią a zdawalnością egzaminu. Rozkład danych przedstawia tabeli kontyngencji:}
=nie). Na podstawie tej próby chcielibyśmy się dowiedzieć, czy w badanej populacji istnieje zależność pomiędzy płcią a zdawalnością egzaminu. Rozkład danych przedstawia tabeli kontyngencji:}
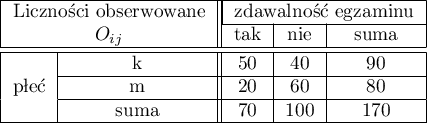
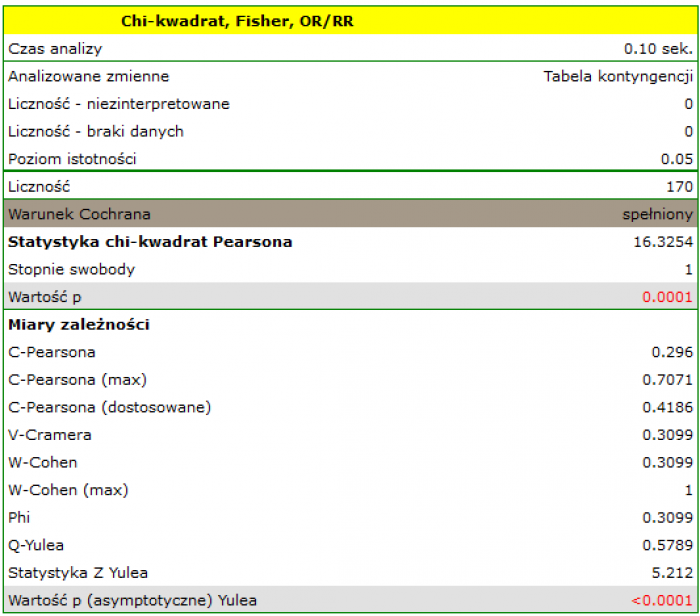
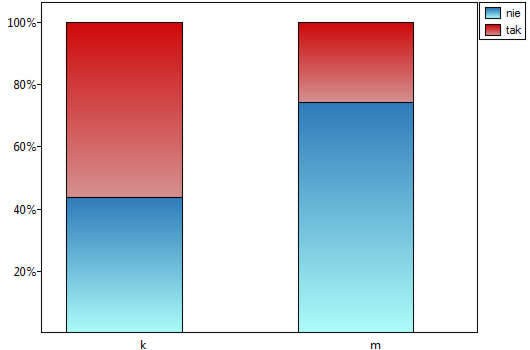
Wartość statystyki testowej wynosi 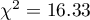 a wyznaczona dla niej wartość
a wyznaczona dla niej wartość 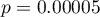 . Uzyskany wynik wskazuje na istnienie zależności statystycznej pomiędzy płcią a zdawalnością egzaminu w badanej populacji.
. Uzyskany wynik wskazuje na istnienie zależności statystycznej pomiędzy płcią a zdawalnością egzaminu w badanej populacji.
Wartość współczynników opartych o test  , a zatem siła związku między badanymi cechami to:
, a zatem siła związku między badanymi cechami to:
Współczynnik kontyngencji 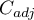 -Pearsona = 0.42.
-Pearsona = 0.42.
Współczynnik kontyngencji 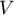 -Cramera =
-Cramera = 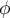 =
=  -Cohena =0.31
-Cohena =0.31
Współczynnik kontyngencji  -Yulea=0.58, a wartość
-Yulea=0.58, a wartość  wykonanego testu
wykonanego testu  podobnie jak poziom istotności testu
podobnie jak poziom istotności testu  wskazuje na istotność statystyczną badanego związku.
wskazuje na istotność statystyczną badanego związku.

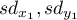 i
i 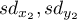 ,
,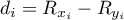 - różnica
- różnica 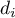 .
.