statpqpl:hotelingpl:hotelling2nzalpl

Test T-kwadrat Hotellinga dla grup niezależnych

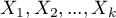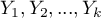Służy do weryfikacji hipotezy o równości średnich badanych $k$ zmiennych $X_1,X_2,...,X_k$ z populacji pierwszej i średnich tych samych $k$ zmiennych $Y_1,Y_2,...,Y_k$ z populacji drugiej.

Podstawowe warunki stosowania:

pomiar na skali interwałowej,
wielowymiarowy rozkład normalny w obu populacjach lub normalność rozkładu każdej badanej zmiennej w obu populacjach,
model niezależny,
równość wariancji badanych zmiennych obu populacji lub równość macierzy kowariancji - warunek szczególnie istotny w przypadku grup o różnych licznościach - gdy warunek nie jest pełniony, powinna zostać wyznaczona korekta.

Hipotezy:

$\begin{array}{cl} \mathcal{H}_0: & \mu_x=\mu_y,\\ \mathcal{H}_1: & $nie wszystkie $\mu_{xj}=\mu_{yj}, \end{array}$

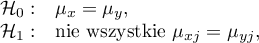
gdzie:

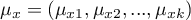$\mu_x=(\mu_{x1}, \mu_{x2},..., \mu_{xk})$ - średnie zmiennych w populacji pierwszej,

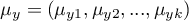$\mu_y=(\mu_{y1}, \mu_{y2},..., \mu_{yk})$ - średnie zmiennych w populacji drugiej.

Statystyka testowa ma postać:

$\begin{displaymath} F=\frac{n-k}{k(n-1)}T^2 \end{displaymath}$

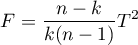
gdzie:

$n=n_x+n_y-1$ ,

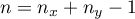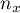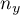$n_x$ , $n_y$ - liczności pierwszej i drugiej próby (liczności poszczególnych zmiennych takie same) ,

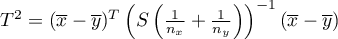$T^2 = (\overline{x}-\overline{y})^T\left(S\left(\frac{1}{n_x}+\frac{1}{n_y}\right)\right)^{-1}(\overline{x}-\overline{y})$ - pierwotna statystyka testowa Hotellinga o rozkładzie $\chi^2$ (zalecana dla prób o dużych licznościach),

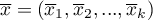$\overline{x}=(\overline{x}_1, \overline{x}_2,..., \overline{x}_k)$ - średnie zmiennych w próbie pierwszej,

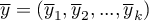$\overline{y}=(\overline{y}_1, \overline{y}_2,..., \overline{y}_k)$ - średnie zmiennych w próbie drugiej,

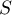$S$ - macierz kowariancji wspólna (ang. pooled) dla obu prób.

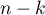Statystyka ta podlega rozkładowi F Snedecora z $k$ i $n-k$ stopniami swobody.

Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

Gdy po wykonanej analizie szukamy zmiennych, których dotyczą różnice, wyznaczamy jednoczesne przedziały ufności dla różnic średnich

$\begin{displaymath} \overline{x}_j-\overline{y}_j\pm\sqrt{\frac{k(n-1)}{n-k}F_{\alpha,df_1,df_2}}\cdot SE_{(diff)_j} \end{displaymath}$

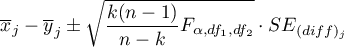
lub przedziały z poprawką Bonferroniego, w celu sprawdzenia czy znajduje się w nich wartość 0. Jeśli bowiem różnica może wynosić 0 to oznacza, że w rzeczywistości różnica pomiędzy badanymi wartościami może nie istnieć. Stosując tą metodę należy pamiętać, że wyznaczone przedziały nie uwzględniają powiązań pomiędzy zmiennymi (które uwzględnia test Hotellinga) a jedynie wielokrotne testowanie.

Szukając zmiennych, których dotyczą różnice możemy również zastosować podejście jednowymiarowe. Wykonujemy wówczas porównania testem t-Studenta dla grup niezależnych oddzielnie dla poszczególnych zmiennych. Niestety, nie uwzględnimy tym samym wzajemnych powiązań, ale uzyskane wartości $p$ testu $t$ -Studenta możemy skorygować w dziale Wielokrotne porównania.

Uwaga!

Zasada działania testu Hotellinga jest tożsama z budową „wielowymiarowych elips” przedziałów ufności wokół centrów wyznaczonych przez średnie (patrz przykład interpretacji elipsy testu Hotellinga dla pojedynczej próby). Przez co, stosując analizę jednowymiarową (nie uwzględniającą wzajemnych powiązań między zmiennymi) często nie jesteśmy w stanie uzyskać tożsamych wyników.

Okno z ustawieniami opcji testu Hotellinga dla grup niezależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→T-kwadrat Hotellinga dla grup niezależnych.

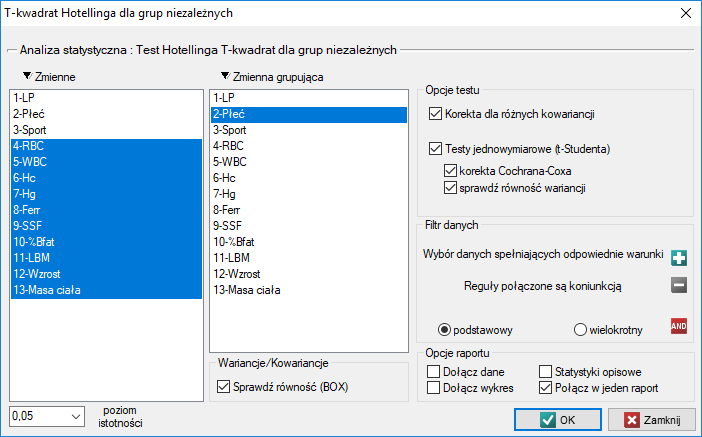
Przykład c.d. (plik sport.pqs)