Spis treści
Cluster Analysis
Cluster analysis is a series of methods for dividing objects or features (variables) into similar groups. In general, these methods are divided into two classes: hierarchical methods and non-hierarchical methods such as the k-means method. In their algorithms, both methods use a similarity matrix to create clusters based on it.
Object grouping and variable grouping are done in cluster analysis in exactly the same way. In this chapter, clustering methods will be explained using object clustering as an example.
Note!
In order to ensure balanced influence of all variables on similarity matrix elements, data should be standardized by choosing appropriate option in the analysis window. Lack of standardization gives more influence on obtained result to variables expressed with higher numbers.
Hierarchical methods
Hierarchical cluster analysis methods involve building a hierarchy of clusters, starting from the smallest (consisting of single objects) and ending with the largest (consisting of the maximum number of objects). Clusters are created on the basis of object similarity matrix.
AGGLOMERATION PROCEDURE
- By following the indicated linkage method, the algorithm finds a pair of similar objects in the similarity matrix and combines them into a cluster;
- The dimension of the similarity matrix is reduced by one (two objects are replaced by one) and the distances in the matrix are recalculated;
- Steps 2-3 are repeated until a single cluster containing all objects is obtained.
Object similarity
In the process of working with cluster analysis, similarity or distance measures play an essential role. The mutual similarity of objects is placed in the similarity matrix. A large variety of methods for determining the distance/similarity between objects allows to choose such measures that best reflect the actual relation. Distance and similarity measures are described in more detail in the section similarity matrix. Cluster analysis is based on finding clusters inside a similarity matrix. Such a matrix is created in the course of performing cluster analysis. For the cluster analysis to be successful, it is important to remember that higher values in the similarity matrix should indicate greater variation of objects, and lower values should indicate their similarity.
Note!
To increase the influence of the selected variables on the elements of the similarity matrix, indicate the appropriate weights when defining the distance while remembering to standardize the data.
For example, for people wanting to take care of a dog, grouping dogs according to size, coat, tail length, character, breed, etc. will make the choice easier. However, treating all characteristics identically may put completely dissimilar dogs into one group. For most of us, on the other hand, size and character are more important than tail length, so the similarity measures should be set so that size and character are most important in creating clusters.
Object and cluster linkage methods
- Single linkage method - the distance between clusters is determined by the distance of those objects of each cluster that are closest to each other.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psline{-}(1.7,0.1)(5.1,-0.4)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imge1a5de3e36c331f92bb1ddd197ffcc63.png)
- Complete linkage method - the distance between clusters is determined by the distance of those objects of each cluster that are farthest apart.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psline{-}(-.8,1)(7.2,1.2)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imgd86738754d560f3b0b517c3b97807da1.png)
- Unweighted pair-group method using arithmetic averages - the distance between clusters is determined by the average distance between all pairs of objects located within two different clusters.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psline{-}(-.8,1)(7.2,1.2)
\psline{-}(-.8,1)(5.1,-0.4)
\psline{-}(-.8,1)(5.6,1.3)
\psline{-}(1.7,0.1)(7.2,1.2)
\psline{-}(1.7,0.1)(5.1,-0.4)
\psline{-}(1.7,0.1)(5.6,1.3)
\psline{-}(0.6,1.2)(7.2,1.2)
\psline{-}(0.6,1.2)(5.1,-0.4)
\psline{-}(1.7,0.1)(5.6,1.3)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img74722956ba453f9c18004ab4885a71f4.png)
- Weighted pair-group metod using arithmetic averages - similarly to the unweighted pair-group method using arithmetic averages method it involves calculating the average distance, but this average is weighted by the number of elements in each cluster. As a result, we should choose this method when we expect to get clusters with similar sizes.
- Ward's method - is based on the variance analysis concept - it calculates the difference between the sums of squares of deviations of distances of individual objects from the center of gravity of clusters, to which these objects belong. This method is most often chosen due to its quite universal character.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\psline[linestyle=dashed]{-}(-.8,1)(0.52,0.8)
\psline[linestyle=dashed]{-}(1.7,0.1)(0.52,0.8)
\psline[linestyle=dashed]{-}(0.6,1.2)(0.52,0.8)
\psdot[dotstyle=pentagon*,linecolor=red](0.52,0.8)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psdot[dotstyle=pentagon*,linecolor=red](5.85,0.8)
\psline[linestyle=dashed]{-}(7.2,1.2)(5.85,0.8)
\psline[linestyle=dashed]{-}(5.1,-0.4)(5.85,0.8)
\psline[linestyle=dashed]{-}(5.6,1.3)(5.85,0.8)
\psline[linestyle=dotted]{-}(0.52,0.8)(5.85,0.8)
\psline[linestyle=dotted]{-}(-.8,1)(7.2,1.2)
\psline[linestyle=dotted]{-}(-.8,1)(5.1,-0.4)
\psline[linestyle=dotted]{-}(-.8,1)(5.6,1.3)
\psline[linestyle=dotted]{-}(1.7,0.1)(7.2,1.2)
\psline[linestyle=dotted]{-}(1.7,0.1)(5.1,-0.4)
\psline[linestyle=dotted]{-}(1.7,0.1)(5.6,1.3)
\psline[linestyle=dotted]{-}(0.6,1.2)(7.2,1.2)
\psline[linestyle=dotted]{-}(0.6,1.2)(5.1,-0.4)
\psline[linestyle=dotted]{-}(1.7,0.1)(5.6,1.3)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img169789b519f1a291561b77a1301c7fc1.png)
The result of a cluster analysis conducted using the hierarchical method is represented using a dendogram. A Dendogram is a form of a tree indicating the relations between particular objects obtained from the similarity matrix analysis. The cutoff level of the dendogram determines the number of clusters into which we want to divide the collected objects. The choice of the cutoff is determined by specifying the length of the bond at which the cutoff will occur as a percentage, where 100\% is the length of the last and also the longest bond in the dendogram.
Settings window of the hierarchical cluster analysis is opened via menu Advanced Statistics→Reduction and grouping→Hierarchical Cluster Analysis.
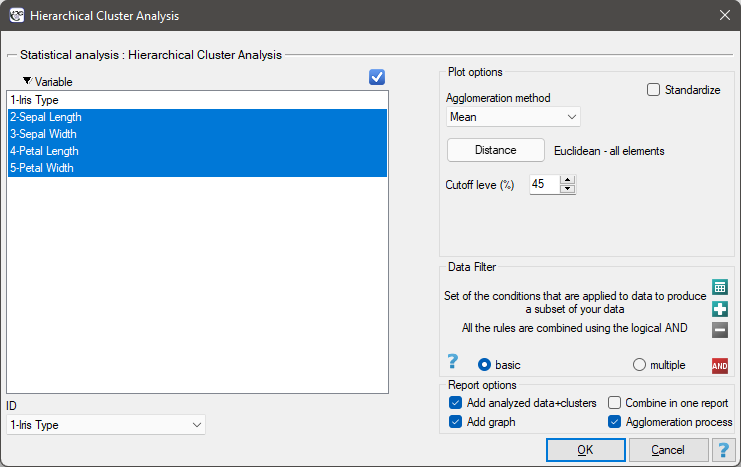
EXAMPLE cont. (iris.pqs file)
The analysis will be performed on the classic data set of dividing iris flowers into 3 varieties based on the width and length of the petals and sepal sepals (R.A. Fisher 19361)). Because this data set contains information about the actual variety of each flower, after performing a cluster analysis it is possible to determine the accuracy of the division made.
We assign flowers to particular groups on the basis of columns from 2 to 5. We choose the way of calculating distances e.g. Euclidean distance and the linkage method. Specifying the cutoff level of clusters will allow us to cut off the dendogram in such a way that clusters will be formed - in the case of this analysis we want to get 3 clusters and to achieve this we change the cutoff level to 45. We will also attach data+clusters to the report..
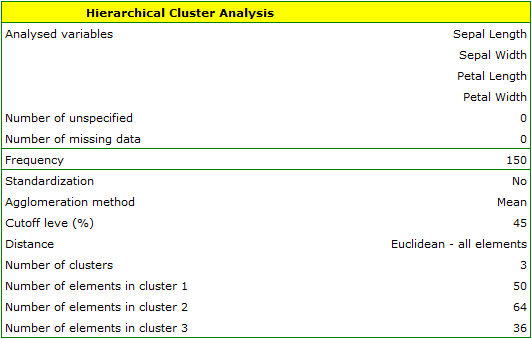
In the dendogram, the order of the bonds and their lengths are shown.
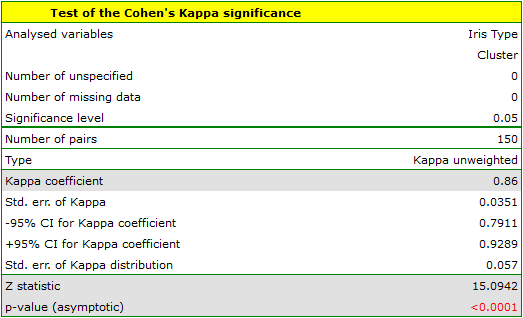
To examine whether the extracted clusters represent the 3 actual varieties of iris flowers, we can copy the column containing the information about cluster belonging from the report and paste it into the datasheet. Like the clusters, the varieties are also described numerically by Codes/Labels/Format, so we can easily perform a concordance analysis. We will check the concordance of our results with the actual belonging of a given flower to the corresponding species using the Cohen's Kappa method .
For this example, the observed concordance is shown in the table:
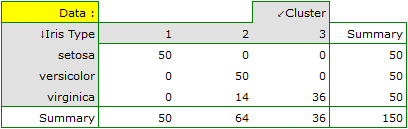
We conclude from it that the virginica variety can be confused with the versicolor variety, hence we observe 14 misclassifications. However, the Kappa concordance coefficient is statistically significant at 0.86, indicating that the clusters obtained are highly consistent with the actual flower variety.
K-means method
K-means method is based on an algorithm initially proposed by Stuart Lloyd and published in 1982 2). In this method, objects are divided into a predetermined number of  clusters. The initial clusters are adjusted during the agglomeration procedure by moving objects between them so that the variation of objects within the cluster is as small as possible and the cluster distances are as large as possible. The algorithm works on the basis of the matrix of Euclidean distances between objects, and the parameters necessary in the procedure of agglomeration of the k-means method are: starting centers and stopping criterion. The starting centers are the objects from which the algorithm will start building clusters, and the stopping criterion is the definition of how to stop the algorithm.
clusters. The initial clusters are adjusted during the agglomeration procedure by moving objects between them so that the variation of objects within the cluster is as small as possible and the cluster distances are as large as possible. The algorithm works on the basis of the matrix of Euclidean distances between objects, and the parameters necessary in the procedure of agglomeration of the k-means method are: starting centers and stopping criterion. The starting centers are the objects from which the algorithm will start building clusters, and the stopping criterion is the definition of how to stop the algorithm.
AGGLOMERATION PROCEDURE
- Selection of starting centers
- Based on the similarity matrix, the algorithm assigns each object to the nearest center
- For the clusters obtained, the adjusted centers are determined.
- Steps 2-3 are repeated until the stop criterion is met.
Starting centers
The choice of starting centers has a major impact on the convergence of the k-means algorithm for obtaining appropriate clusters. The starting centers can be selected in two ways:
- k-means++ - is the optimal selection of starting points by using the k-means++ algorithm proposed in 2007 by David Arthur and Sergei Vassilvitskii 3). It ensures that the optimal solution of the k-means algorithm is obtained with as few iterations as possible. The algorithm uses an element of randomness in its operation, so the results obtained may vary slightly with successive runs of the analysis. If the data do not form into natural clusters, or if the data cannot be effectively divided into disconnected clusters, using k-means++ will result in completely different results in subsequent runs of the k-means analysis. High reproducibility of the results, on the other hand, demonstrates the possibility of good division into separable clusters.
- n firsts - allows the user to indicate points that are start centers by placing these objects in the first positions in the data table.
Stop criterion is the moment when the belonging of the points to the classes does not change or the number of iterations of steps 2 and 3 of the algorithm reaches a user-specified number of iterations.
Because of the way the k-means cluster analysis algorithm works, a natural consequence of it is to compare the resulting clusters using a one-way analysis of variance (**ANOVA**) for independent groups.
Settings window of the k-means cluster analysis is opened via menu Advanced Statistics→Reduction and grouping→K-means cluster analysis.
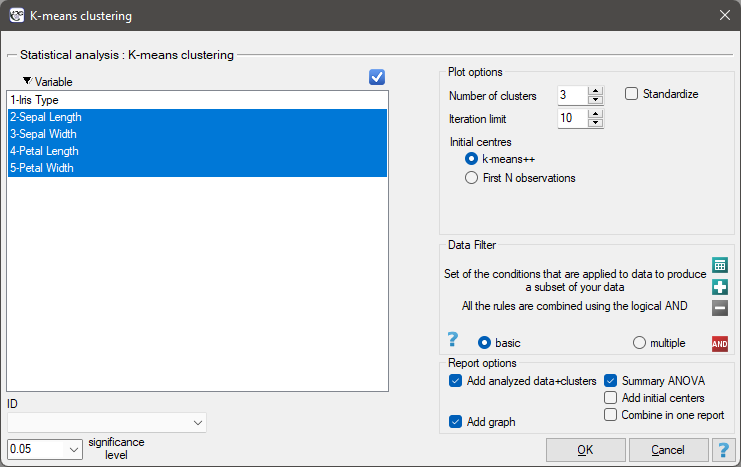
EXAMPLE cont. (iris.pqs file)
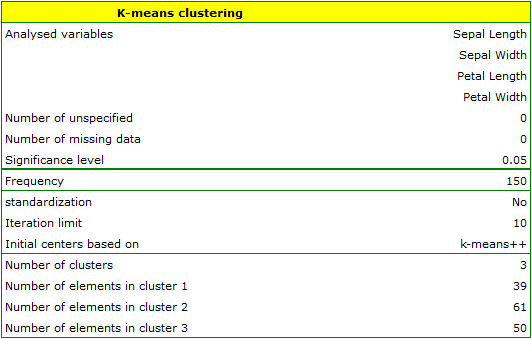
The analysis will be performed on the classic data set of dividing iris flowers into 3 varieties based on the width and length of the petals and sepal sepals (R.A. Fisher 19364)).
We assign flowers to particular groups on the basis of columns from 2 to 5. We also indicate that we want to divide the flowers into 3 groups. As a result of the analysis, 3 clusters were formed, which differed statistically significantly in each of the examined dimensions (ANOVA results), i.e. petal width, petal length, sepal width as well as sepal length.
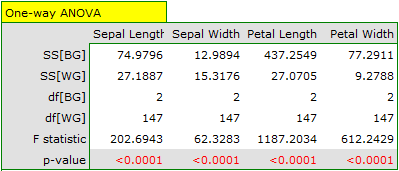
The difference can be observed in the graphs where we show the belonging of each point to a cluster in the two dimensions selected:
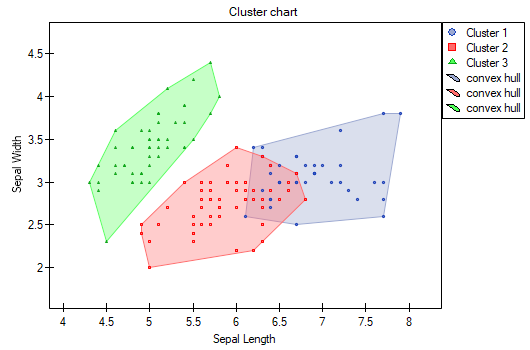
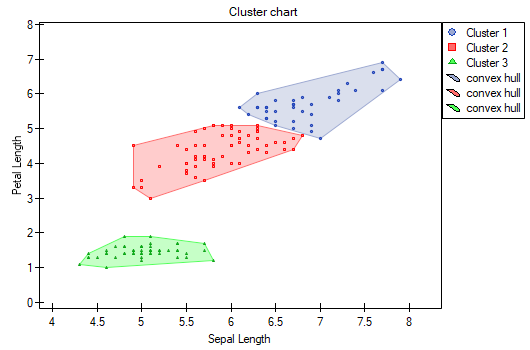
By repeating the analysis we may get slightly different results, but the variation obtained will not be large. It proves that data subjected to analysis form natural clusters and conducting a cluster analysis is justified in this case.
Note no.1!
After running the analysis a few times, we can select the result we are most interested in, and then set those data that are the starting centers at the beginning of the worksheet - then the analysis performed based on the starting centers selected as N first observations will consistently produce that result we selected.
Note no.2!
To find out if the clusters represent the 3 actual varieties of iris flowers, we can copy the information about belonging to a cluster from the report and paste it into the datasheet. We can check the consistency of our results with the actual affiliation of a given flower to the corresponding variety in the same way as for the hierarchical cluster analysis.