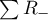Test Wilcoxona (kolejności par)
Test kolejności par Wilcoxona (ang. Wilcoxon matched-pairs test), znany również pod nazwą testu Wilcoxona dla grup zależnych, Wilcoxon (19451),19492)). Stosuje się go w sytuacji gdy pomiarów badanej zmiennej dokonujemy dwukrotnie w różnych warunkach. Jest on rozszerzeniem na dwie zależne próby testu rangowanych znaków Wilcoxona (przeznaczonego dla jednej próby). Interesuje nas różnica pomiędzy parami pomiarów badanej cechy (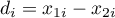 ) dla każdego z
) dla każdego z  badanych obiektów. Różnica ta wykorzystywana jest do weryfikacji hipotezy o tym, że mediana dla niej (dla różnicy) w badanej populacji wynosi 0.
badanych obiektów. Różnica ta wykorzystywana jest do weryfikacji hipotezy o tym, że mediana dla niej (dla różnicy) w badanej populacji wynosi 0.
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości sumy rang dodatnich i ujemnych lub są upraszczane do median:
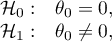
gdzie:
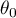 to - mediana
to - mediana 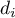 w populacji.
w populacji.
Wyznaczamy wartość statystyki testowej, a na jej podstawie wartość  , którą porównujemy z poziomem istotności
, którą porównujemy z poziomem istotności  :
:

Uwaga!
W zależności od wielkości próby statystyka testowa przyjmuje inną postać:
- Dla małej liczności próby
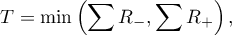
Statystyka ta podlega rozkładowi Wilcoxona i nie zawiera poprawki na rangi wiązane.
- Dla próby o dużej liczności
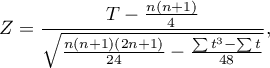
Wzór na statystykę testową  zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 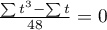 ).
).
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Poprawka na ciągłość testu Wilcoxona (Marascuilo and McSweeney (1977)3))
Poprawkę na ciągłość stosujemy by zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu normalnego. Wzór na statystykę testową z poprawką na ciągłość wyraża się wtedy wzorem:
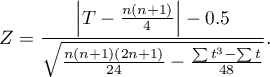
Uwaga! Od wersji 1.8.0 mediana wyliczana w dla kolumny różnica obejmuje wszystkie pary wyników za wyjątkiem tych, których różnica wynosi 0.
Standaryzowana wielkość efektu
Rozkład statystyki testu Wilcoxona jest aproksymowany przez rozkłady normalny, który można przekształcić na wielkość efektu 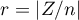 4) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
4) by następnie uzyskać wartość d-Cohena zgodnie ze standardową konwersją stosowaną przy meta-analizach:
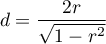
Przy interpretacji efektu badacze często posługują się ogólnymi, określonymi przez Cohena 5) wskazówkami definiującymi małą (0.2), średnią (0.5) i dużą (0.8) wielkość efektu.
Okno z ustawieniami opcji testu Wilcoxona dla grup zależnych wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Wilcoxon (kolejności par) lub poprzez ''Kreator''.
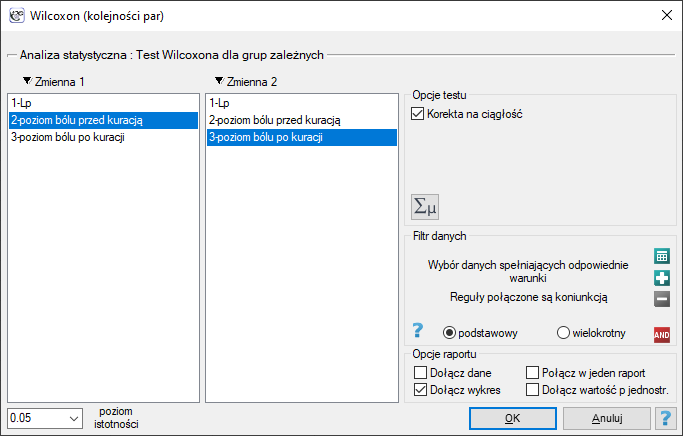
Pobrano próbę 22 pacjentów cierpiących na raka. Badano u nich poziom odczuwanego bólu (na skali od 1 do 10, gdzie 1 to brak bólu a 10 to ból największy). Badanie to powtórzono po miesiącu stosowania kuracji nowym lekiem mającym obniżyć poziom odczuwanego bólu. Otrzymano następujące wyniki:
(przed, po): (2, 2) (2, 3) (3, 1) (3,1) (3, 2) (3, 2) (3, 3) (4, 1) (4, 3) (4, 4) (5, 1) (5, 1) (5, 2) (5, 4) (5, 4) (6, 1) (6, 3) (7, 2) (7, 4) (7, 4) (8, 1) (8, 3). Chcemy sprawdzić, czy zastosowana kuracja ma wpływ na poziom odczuwanego bólu w populacji z której pochodzi próba.
Hipotezy:

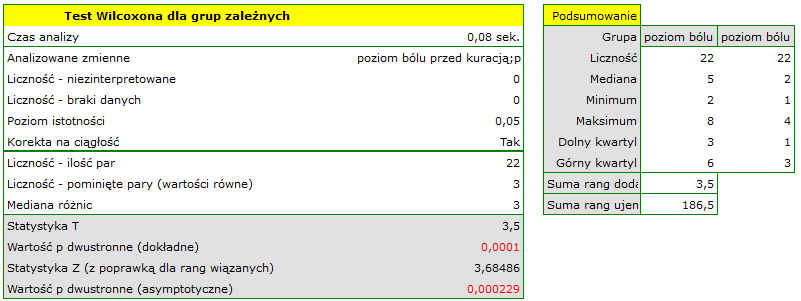
Porównując wartość 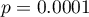 testu Wilcoxona opartego o statystykę
testu Wilcoxona opartego o statystykę 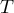 z poziomem istotności
z poziomem istotności  stwierdzamy, że istnieje ważna statystycznie różnica w poziomie odczuwanego bólu pomiędzy dwoma badaniami. Różnica te polega na tym, że poziom bólu spadł (suma rang ujemnych jest znacznie większa niż suma rang dodatnich). Taką samą decyzję podjęlibyśmy również na podstawie wartości
stwierdzamy, że istnieje ważna statystycznie różnica w poziomie odczuwanego bólu pomiędzy dwoma badaniami. Różnica te polega na tym, że poziom bólu spadł (suma rang ujemnych jest znacznie większa niż suma rang dodatnich). Taką samą decyzję podjęlibyśmy również na podstawie wartości 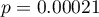 lub
lub 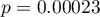 testu Wilcoxona opartego o statystykę
testu Wilcoxona opartego o statystykę  lub
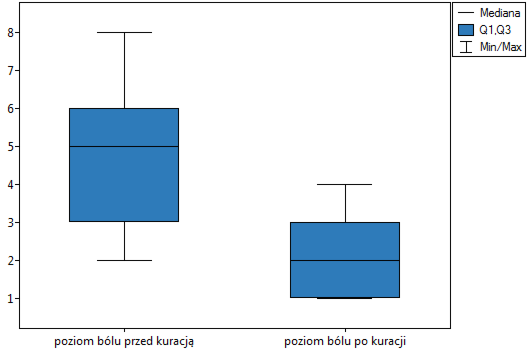
lub  z poprawką na ciągłość. Różnice możemy zaobserwować na wykresie typu ramka-wąsy lub wykresie kolumnowym.
z poprawką na ciągłość. Różnice możemy zaobserwować na wykresie typu ramka-wąsy lub wykresie kolumnowym.

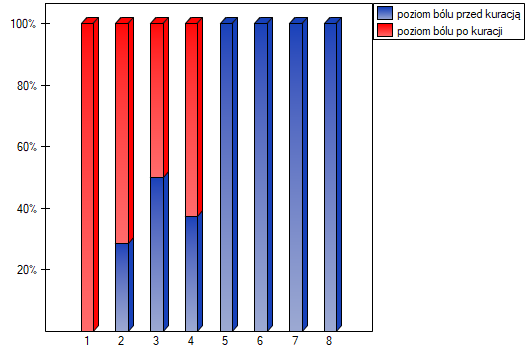
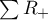
 suma
suma