ANOVA Q-Cochrana
Analiza wariancji Q-Cochrana oparta na teście Q-Cochrana (ang. Q-Cochran test) opisana została przez Cochrana (1950)1). Test ten jest rozszerzeniem testu McNemara do 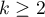 grup zależnych. Służy do weryfikacji hipotezy o symetryczności pomiędzy wynikami kilkukrotnych pomiarów
grup zależnych. Służy do weryfikacji hipotezy o symetryczności pomiędzy wynikami kilkukrotnych pomiarów 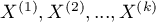 cechy
cechy  . Badana cecha może mieć tylko 2 wartości, do których (dla potrzeb analizy) przypisywane są liczby 0 i 1.
. Badana cecha może mieć tylko 2 wartości, do których (dla potrzeb analizy) przypisywane są liczby 0 i 1.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej (zmienne dychotomiczne, czyli zmienne o 2 kategoriach),
Hipotezy:
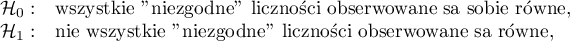
gdzie:
„niezgodne” liczności obserwowane, to liczności obserwowane wyliczone, gdy wartość badanej cechy jest różna w kolejnych pomiarach.
Statystyka testowa ma postać:
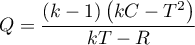
gdzie:
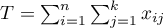 ,
,
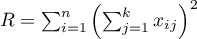 ,
,
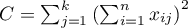 ,
,
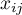
 wartość
wartość  -tego pomiaru dla
-tego pomiaru dla  -tego obiektu (czyli 0 lub 1).
-tego obiektu (czyli 0 lub 1).
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru: 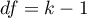 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC przeprowadzone zostało w rozdziale dotyczącym jednoczynnikowej analizy wariancji.
Stosowany dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
Hipotezy:
Przykład - porównania proste (dla różnicy proporcji 1 wybranej pary pomiarów):
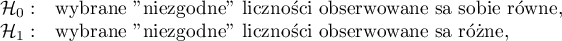
 Wartość najmniejszej istotnej różnicy wyliczana jest ze wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest ze wzoru:
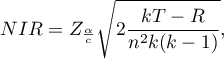
gdzie:
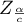 - to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności poziomu istotności
- to wartość krytyczna (statystyka) rozkładu normalnego dla poziomu istotności poziomu istotności  skorygowanego o liczbę możliwych porównań prostych
skorygowanego o liczbę możliwych porównań prostych  .
.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
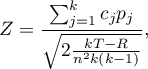
gdzie:
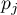
 proporcja
proporcja  -tego pomiaru
-tego pomiaru  ,
,
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład normalny, a wartość  jest korygowana o liczbę możliwych porównań prostych
jest korygowana o liczbę możliwych porównań prostych  .
.
Okno z ustawieniami opcji ANOVA Q Cochrana wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Q Cochrana lub poprzez ''Kreator''.
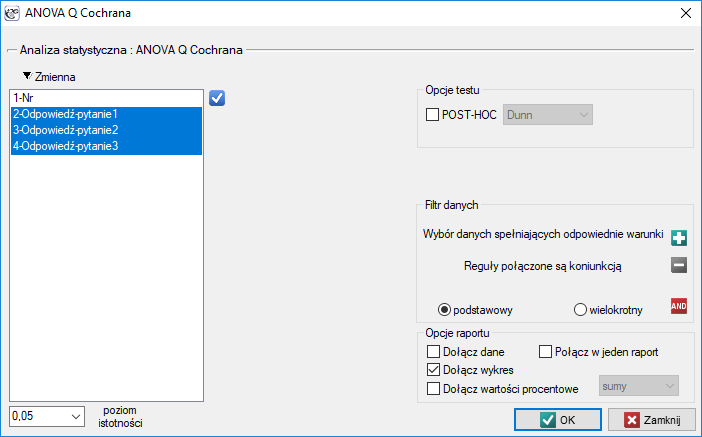
Uwaga!
Test ten jest możliwy do wyliczenia tylko na podstawie danych surowych.
Chcemy porównać trudność 3 pytań testowych. W tym celu z badanej populacji osób, do których adresowany jest test wybieramy 20 osobową próbę. Każda osoba z próby daje odpowiedzi na 3 pytania zawarte w teście. Następnie sprawdzamy poprawność tych odpowiedzi (osoba może odpowiedzieć poprawnie lub błędnie). Wyniki zawiera poniższa tabela:
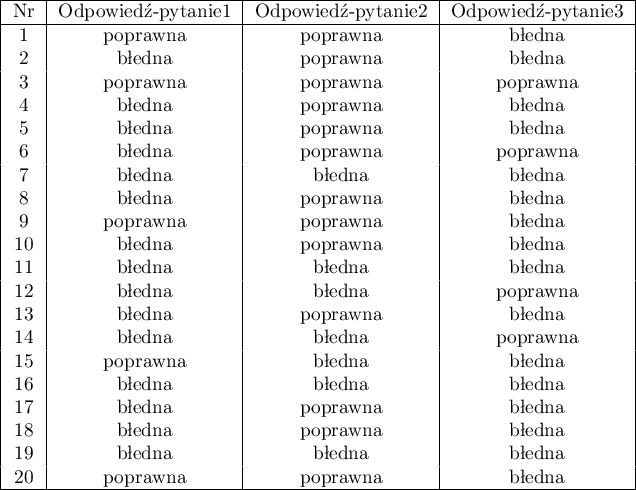
Hipotezy:

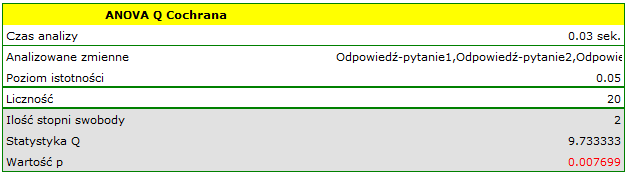
Porównując wartość 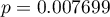 z poziomem istotności
z poziomem istotności  stwierdzamy, że pytanie testowe wykazują różny stopień trudności. Wznawiamy analizę przyciskiem
stwierdzamy, że pytanie testowe wykazują różny stopień trudności. Wznawiamy analizę przyciskiem  by wykonać test POST-HOC i w oknie opcji testu wybieramy POST-HOC
by wykonać test POST-HOC i w oknie opcji testu wybieramy POST-HOC Dunn.
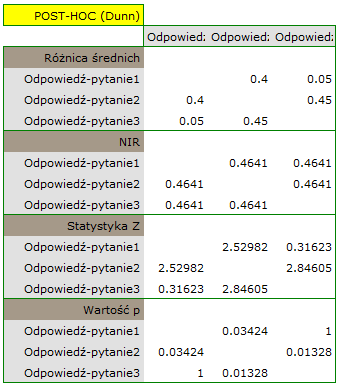
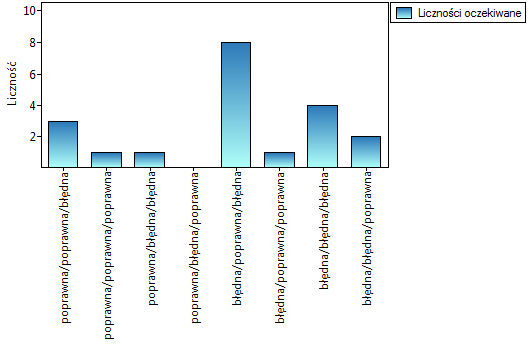
Wykonana analiza POST-HOC wskazuje, że różnice dotyczą pytania 2 i 1 oraz 2 i 3. Różnica ta polega na tym, że pytanie 2 jest łatwiejsze niż 1 i 3 (liczba poprawnych odpowiedzi jest tu wyższa).