Testy chi-kwadrat
Testy te opierają się na danych zebranych w postaci tabeli kontyngencji 2 cech, cechy X i cechy Y, z których pierwsza ma  a druga
a druga  kategorii, a więc powstała tabela ma
kategorii, a więc powstała tabela ma  wierszy i
wierszy i  kolumn. Z tego względu możemy mówić o teście chi-kwadrat 2×2 (dla tabel o dwóch wierszach i dwóch kolumnach) lub o teście chi-kwadrat RxC (o wielu wierszach i kolumnach).
kolumn. Z tego względu możemy mówić o teście chi-kwadrat 2×2 (dla tabel o dwóch wierszach i dwóch kolumnach) lub o teście chi-kwadrat RxC (o wielu wierszach i kolumnach).
Szczegółowe informacje na temat testu chi-kwadrat dwóch cech możemy przeczytać tutaj:
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę,
Dodatkowy warunek dla testu  :
:
Hipotezy w brzmieniu ogólnym:
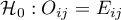 dla wszystkich kategorii,
dla wszystkich kategorii,
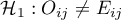 dla przynajmniej jednej kategorii.
dla przynajmniej jednej kategorii.
gdzie:
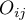
 liczności obserwowane w tabeli kontyngencji,
liczności obserwowane w tabeli kontyngencji,
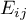
 liczności oczekiwane w tabeli kontyngencji.
liczności oczekiwane w tabeli kontyngencji.
Hipotezy w brzmieniu testu niezależności:
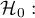 nie istnieje zależność pomiędzy badanymi cechami populacji (obie klasyfikacje ze względu na cechę X i na cechę Y są statystycznie niezależne),
nie istnieje zależność pomiędzy badanymi cechami populacji (obie klasyfikacje ze względu na cechę X i na cechę Y są statystycznie niezależne),
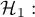 istnieje zależność pomiędzy badanymi cechami populacji.
istnieje zależność pomiędzy badanymi cechami populacji.
Wyznaczoną wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Dodatkowo
Oprócz testu chi-kwadrat może zajść konieczność wyznaczenia innego, pokrewnego testu. W przypadku gdy warunek Cochrana nie jest spełniony można wyznaczyć:
W przypadku gdy uzyskamy tabelę Rx2, i kategorie R można uporządkować, możliwe jest wyznaczanie trendu:
W przypadku, gdy na podstawie testu wykonanego dla tabeli większej niż 2×2 stwierdzimy występowanie istotnych zależności lub różnic, wówczas można wykonać wielokrotne porównania wraz z odpowiednią korektą porównań wielokrotnych po to, by zlokalizować umiejscowienie tych zależności/różnic. Korekta taka może być dokonana automatycznie, gdy tabela ma wiele kolumn. Wówczas w oknie opcji testu należy zaznaczyć
Wielokrotne porównania kolumn (RxC).W przypadku, gdy chcemy opisać siłę związku między cechą X i cechą Y możemy wyznaczyć:
W przypadku, gdy chcemy opisać dla tabel 2×2 wielkość wpływu czynnika ryzyka możemy wyznaczyć:
