ANOVA Durbina (brakujących danych)
Analiza wariancji powtarzanych pomiarów dla rang Durbina została zaproponowana przez Durbina (1951)1). Test ten stosuje się w sytuacji, gdy pomiarów badanej zmiennej dokonujemy kilkukrotnie - czyli w podobnej sytuacji w jakiej stosowana jest ANOVA Friedmana. Oryginalny test Durbina i test Friedmana dają ten sam wynik w sytuacji, gdy dysponujemy kompletnym zestawem danych. Test Durbina ma jednak pewną przewagę - można go również wyliczać dla niekompletnego zestawu danych. Przy czym braki danych nie mogą być zlokalizowane dowolnie, ale dane muszą tworzyć tzw. zbalansowany i niekompletny blok, czyli:
- liczba pomiarów dla każdego obiektu wynosi
 (
(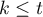 ),
), - każdy pomiar dokonywany jest na
 obiektach (
obiektach (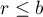 ),
), - liczba obiektów dla których wykonano jednocześnie tą sama parę pomiarów jest stała i wynosi
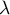 .
.
gdzie:
 - łączna liczba rozpatrywanych pomiarów,
- łączna liczba rozpatrywanych pomiarów,
 - łączna liczba badanych obiektów
- łączna liczba badanych obiektów
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej,
Hipotezy dotyczą równości sumy rang dla kolejnych pomiarów (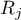 ) lub są upraszczane do median (
) lub są upraszczane do median (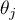 ):
):
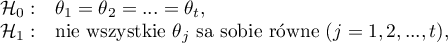
Wyznacza się dwie statystyki testowe o następującej postaci:
![LaTeX \begin{displaymath}
T_1=\frac{(t-1)\left[\sum_{j=1}^tR_j^2-tC\right]}{A-C},
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img6263bdbeddade6aabd733985ed7a7916.png)
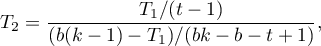
gdzie:
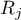 - suma rang dla kolejnych pomiarów
- suma rang dla kolejnych pomiarów 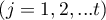 ,
,
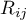 - rangi przypisane kolejnym pomiarom, oddzielnie dla każdego z badanych obiektów
- rangi przypisane kolejnym pomiarom, oddzielnie dla każdego z badanych obiektów 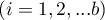 ,
,
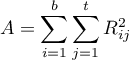
 suma kwadratów dla rang,
suma kwadratów dla rang,
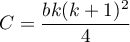
 współczynnik korekcji.
współczynnik korekcji.
Wzór na statystykę 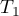 i
i 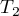 zawiera poprawkę na rangi wiązane.
zawiera poprawkę na rangi wiązane.
W przypadku danych kompletnych statystyka 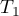 jest tożsama z testem Friedmana. Ma ona asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z
jest tożsama z testem Friedmana. Ma ona asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 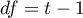 stopniami swobody.
stopniami swobody.
Statystyka 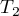 to odpowiednik korekty Iman-Davenport ANOVA Friedmana, więc podlega rozkładowi F Snedecora z
to odpowiednik korekty Iman-Davenport ANOVA Friedmana, więc podlega rozkładowi F Snedecora z 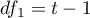 i
i  stopniami swobody. Uznaje się ją obecnie za bardziej precyzyjną niż statystykę
stopniami swobody. Uznaje się ją obecnie za bardziej precyzyjną niż statystykę 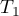 i rekomenduje jej stosowanie2).
i rekomenduje jej stosowanie2).
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC przeprowadzone zostało w rozdziale dotyczącym jednoczynnikowej analizy wariancji.
Stosowany dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
Hipotezy:
Przykład - porównania proste (porównanie pomiędzy sobą 2 wybranych median / sum rang):
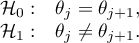
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
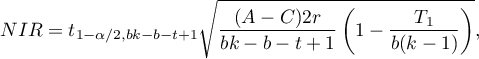
gdzie:
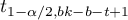 - to wartość krytyczna (statystyka) rozkładu t-Studenta dla poziomu istotności
- to wartość krytyczna (statystyka) rozkładu t-Studenta dla poziomu istotności  i
i 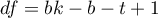 stopni swobody.
stopni swobody.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
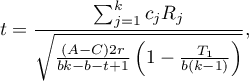
Statystyka ta podlega rozkładowi t-Studenta z 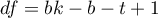 stopniami swobody.
stopniami swobody.
Okno z ustawieniami opcji ANOVA Durbina wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Friedmana (możliwość braków danych) lub poprzez Kreator.
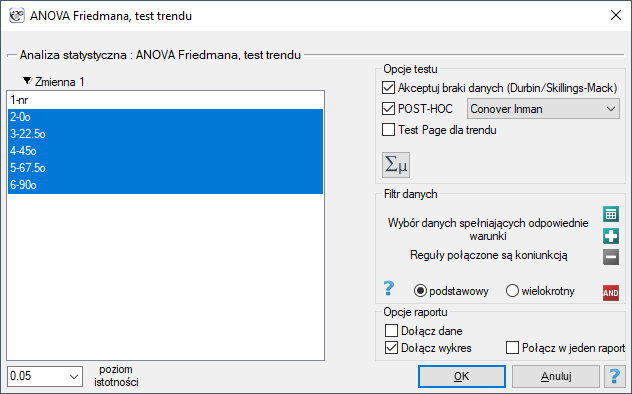
Uwaga!
By rekordy w których występują braki danych były brane pod uwagę wymagane jest zaznaczenie opcji Akceptuj braki danych. Jako braki danych traktowane są puste komórki oraz komórki o wartościach nieliczbowych. W analizie biorą udział tylko rekordy zawierające więcej niż jedną wartość liczbową.
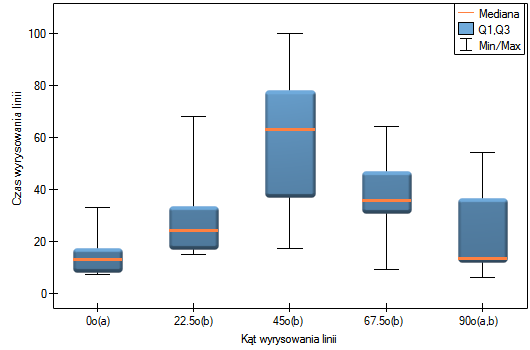
Przeprowadzono eksperyment wśród 20 pacjentów szpitala psychiatrycznego (Ogilvie 1965 3)). Eksperyment ten polegał na odrysowaniu linii prostych według zaprezentowanego wzoru. Wzór przedstawiał 5 linii rysowanych pod różnym kątem (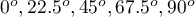 ) względem wskazanego środka. Zadaniem pacjentów było odwzorowanie linii mając zasłoniętą dłoń. Jako wynik eksperymentu zapisano czas w jakim pacjent kreślił daną linię. W idealnym przypadku każdy pacjent kreśliłby linię pod każdym kątem, jednak upływający czas i zmęczenie miałyby znaczny wpływ na wydajność pracy. Ponadto trudno jest utrzymać zainteresowanie pacjenta i chęć współpracy przez dłuższy czas. W związku z tym projekt zaplanowano i przeprowadzono w zbalansowanych i niekompletnych blokach. Każdy z 20 pacjentów wyrysowywał linię pod dwoma kontami (możliwych kątów było pięć). W ten sposób każdy kąt wyrysowywany był ośmiokrotnie. Czas w jakim każdy pacjent wyrysowywał linię pod zadanym kątem zapisano w tabeli.
) względem wskazanego środka. Zadaniem pacjentów było odwzorowanie linii mając zasłoniętą dłoń. Jako wynik eksperymentu zapisano czas w jakim pacjent kreślił daną linię. W idealnym przypadku każdy pacjent kreśliłby linię pod każdym kątem, jednak upływający czas i zmęczenie miałyby znaczny wpływ na wydajność pracy. Ponadto trudno jest utrzymać zainteresowanie pacjenta i chęć współpracy przez dłuższy czas. W związku z tym projekt zaplanowano i przeprowadzono w zbalansowanych i niekompletnych blokach. Każdy z 20 pacjentów wyrysowywał linię pod dwoma kontami (możliwych kątów było pięć). W ten sposób każdy kąt wyrysowywany był ośmiokrotnie. Czas w jakim każdy pacjent wyrysowywał linię pod zadanym kątem zapisano w tabeli.
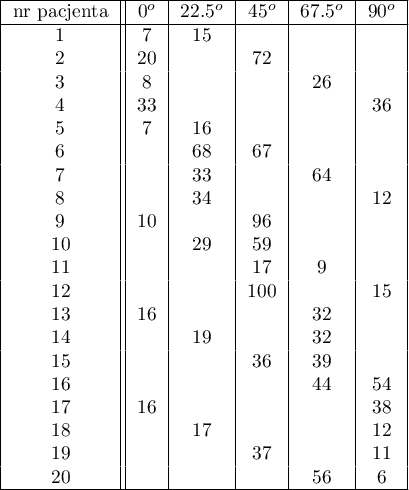
Chcemy sprawdzić, czy czas jaki został poświęcony na wyrysowanie poszczególnych linii jest zupełnie losowy, czy też są linie, których wyrysowywanie zajęło więcej lub mniej czasu.
Hipotezy:
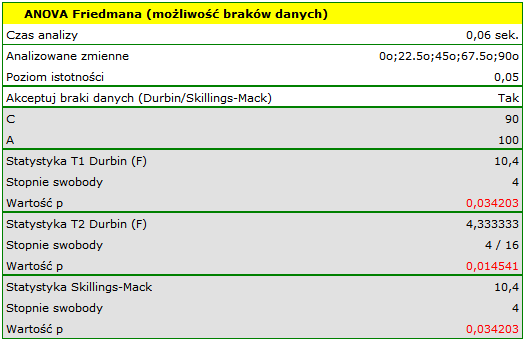
Porównując wartość 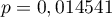 dla statystyki
dla statystyki 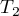 (lub wartość
(lub wartość 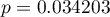 dla statystyki
dla statystyki 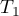 ) z poziomem istotności
) z poziomem istotności  stwierdzamy, że linie nie są rysowane w tym samym czasie. Wykonana analiza POST-HOC wskazuje na różnice czasu poświęconego na narysowanie linii pod kątem
stwierdzamy, że linie nie są rysowane w tym samym czasie. Wykonana analiza POST-HOC wskazuje na różnice czasu poświęconego na narysowanie linii pod kątem 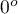 . Jest ona rysowana szybciej niż linie pod kątem
. Jest ona rysowana szybciej niż linie pod kątem 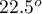 ,
, 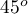 oraz
oraz 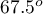 .
.
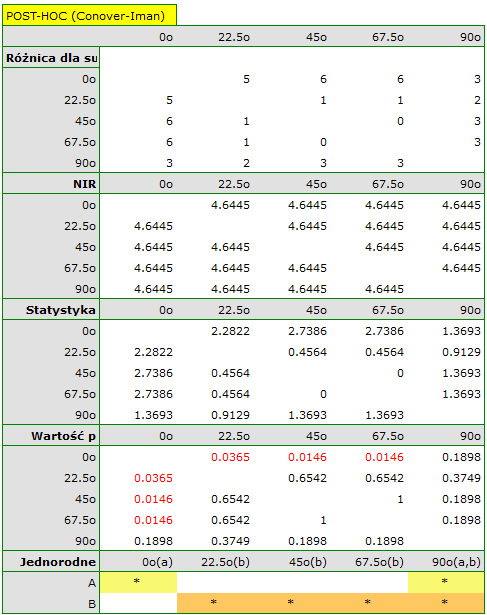
Na wykresie zaznaczono grupy jednorodne wskazane przez test post-hoc.