en:statpqpl:korelpl:parpl:rpporpl

Comparison of correlation coefficients

The test for checking the equality of the Pearson product-moment correlation coefficients, which come from 2 independent populations

This test is used to verify the hypothesis determining the equality of 2 Pearson's linear correlation coefficients (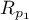 $R_{p_1}$ , $R_{p_2})$ .

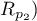Basic assumptions:

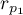$r_{p_1}$ and $r_{p_2}$ come from 2 samples which are chosen randomly from independent populations,
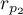$r_{p_1}$ and $r_{p_2}$ describe the strength of dependence of the same features: $X$ and $Y$ ,
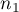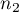sizes of both samples ( $n_1$ and $n_2$ ) are known.

Hypotheses:

$\begin{array}{cl} \mathcal{H}_0: & R_{p_1} = R_{p_2}, \\ \mathcal{H}_1: & R_{p_1} \ne R_{p_2}. \end{array}$

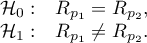
The test statistic is defined by:

$\begin{displaymath} t=\frac{z_{r_{p_1}}-z_{r_{p_2}}}{\sqrt{\frac{1}{n_1-3}+\frac{1}{n_2-3}}}, \end{displaymath}$

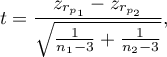
where:

$\displaystyle z_{r_{p_1}}=\frac{1}{2}\ln\left(\frac{1+r_{p_1}}{1-r_{p_1}}\right)$ ,

$\displaystyle z_{r_{p_2}}=\frac{1}{2}\ln\left(\frac{1+r_{p_2}}{1-r_{p_2}}\right)$ .

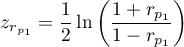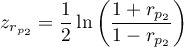The test statistic has the t-Student distribution with 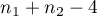$n_1+n_2-4$ degrees of freedom.

The p-value, designated on the basis of the test statistic, is compared with the significance level $\alpha$ :

$\begin{array}{ccl} $ if $ p \le \alpha & \Longrightarrow & $ reject $ \mathcal{H}_0 $ and accept $ \mathcal{H}_1, \\ $ if $ p > \alpha & \Longrightarrow & $ there is no reason to reject $ \mathcal{H}_0. \\ \end{array}$

Note

A comparison of the slope coefficients of the regression lines can be made in a similar way. </WRAP>