en:statpqpl:porown2grpl:parpl:t

The t-test with the Cochran-Cox adjustment

The Cochran-Cox adjustment relates to the t-test for independent groups (1957)¹⁾ and is calculated when variances of analysed variables in both populations are different.

The test statistic is defined by:

$\begin{displaymath} t=\frac{\overline{x}_1-\overline{x}_2}{\sqrt{\frac{sd_1^2}{n_1}+\frac{sd_2^2}{n_2}}}. \end{displaymath}$

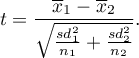
The test statistic has the t-Student distribution with degrees of freedom proposed by Satterthwaite (1946)²⁾ and calculated using the formula:

$\begin{displaymath} df=\frac{\left( \frac{sd_1^2}{n_1}+\frac{sd_2^2}{n_2}\right)^2}{\left( \frac{sd_1^2}{n_1}\right)^2\cdot \frac{1}{(n_1-1)}+\left( \frac{sd_2^2}{n_2}\right)^2\cdot \frac{1}{(n_2-1)}}. \end{displaymath}$

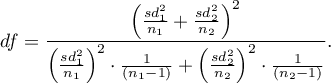
The settings window with the t- test for independent groups can be opened in Statistics menu→Parametric tests→t-test for independent groups or in ''Wizard''.

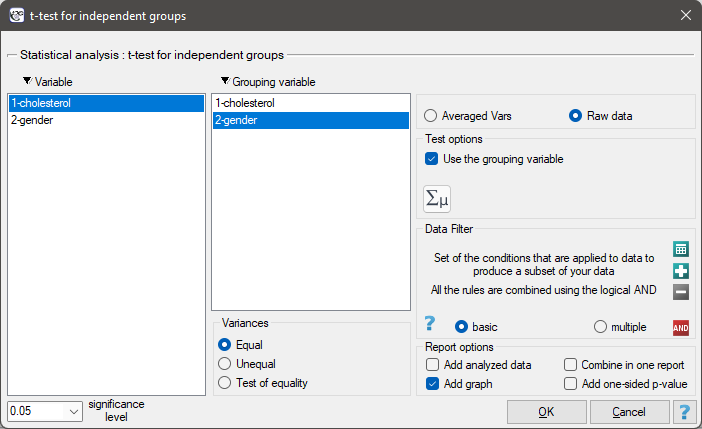
If, in the window which contains the options related to the variances, you have choosen:

equal, the t-test for independent groups will be calculated ,
different, the t-test with the Cochran-Cox adjustment will be calculated,
check equality, to calculate the Fisher-Snedecor test, basing on its result and set the level of significance, the t-test for independent groups with or without the Cochran-Cox adjustment will be calculated.

Note Calculations can be based on raw data or data that are averaged like: arithmetic means, standard deviations and sample sizes.

¹⁾

Cochran W.G. and Cox G.M. (1957), Experimental designs (2nd 4.). New York: John Wiley and Sons.

²⁾

Satterthwaite F.E. (1946), An approximate distribution of estimates of variance components. Biometrics Bulletin, 2, 1 10-1 14