Spis treści
Wykresy
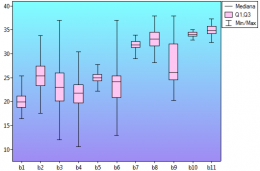
Program PQStat oferuje wykresy kolumnowe, wykresy błędów, wykresy typu ramka-wąsy, punktowe, liniowo-punktowe.
Okno z ustawieniami opcji wykresów wywołujemy poprzez menu Wykresy.
Zmiana podstawowych parametrów wykresu jest możliwa bezpośrednio w oknie wykresu. Jeśli natomiast:
- chcemy zmienić parametry ogólne wykresu takie jak: tytuły, tła, osie, linie siatki czy legendę − wybieramy zakładkę
Ogólne opcje wykresu; - chcemy zmienić wygląd samego rysowanego obiektu np. kształt, styl, kolory − wybieramy zakładkę
Właściwe opcje wykresu; - chcemy narysować dodatkowe elementy na wykresie np. dorysować linię − wybieramy zakładkę
Inne.
Wykresy prezentujące wyniki analiz statystycznych dostępne są w oknie wybranej analizy statystycznej pod opcją Dołącz wykres.
Wykres zwracany jest do raportu, gdzie może być:
- zapisany - opcja
Zapisz wykres jako…z menu kontekstowego; - wydrukowany - opcja
Drukuj wykresz menu kontekstowego; - skopiowany - opcja
Kopiuj wykresz menu kontekstowego; - poddany edycji - dotyczy to
Ogólnych opcji wykresuiWłaściwych opcji wykresu. By edytować wykres wystarczy podwójne kliknięcie myszy na wykresie, lub wybranie opcjiEdytuj wykresz menu kontekstowego. W oknie edycji wykresu możliwe jest również zapisanie wykresu w wysokiej rozdzielczości.
Lokalne techniki wygładzania liniowego
LOWESS
LOWESS (ang.locally weighted scatterplot smoothing) znana również pod nazwą LOESS (ang. locally estimated scatterplot smoothing) jest jedną z wielu „nowoczesnych” metod modelowania opartych na metodzie najmniejszych kwadratów. LOESS łączy w sobie prostotę regresji liniowej z elastycznością regresji nieliniowej. Oszacowanie regresji lokalnej (locally weighted regression) zostało niezależnie wprowadzone na kilku różnych polach pod koniec XIX i na początku XX wieku (Henderson, 1916 1); Schiaparelli, 18662)). W literaturze statystycznej metodę tę wprowadzono niezależnie z różnych punktów widzenia pod koniec lat siedemdziesiątych min. Cleveland, 1979 3). Metoda wykorzystana w programie PQstat opiera się na tej właśnie pracy. Podstawową zasadą jest to, że funkcja gładka może być dobrze przybliżona przez wielomian niskiego stopnia (w programie zastosowano funkcję liniową czyli wielomian pierwszego stopnia) w sąsiedztwie dowolnego punktu x.
Algorytm postępowania:
(1)
Dla każdego punktu zbioru danych budujemy okno zawierające sąsiednie elementy. To jak dużo elementów znajdzie się w oknie wyznacza parametr wygładzania 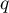 . Czym wyższa jego wartość, tym bardziej wygładzoną uzyskamy funkcję. Jeśli parametr ten wyniesie np. 0.2, wówczas w oknie znajdzie się około 20% danych i one posłużą do budowania wielomianu (tutaj jednomianu tzn. funkcji liniowej).
. Czym wyższa jego wartość, tym bardziej wygładzoną uzyskamy funkcję. Jeśli parametr ten wyniesie np. 0.2, wówczas w oknie znajdzie się około 20% danych i one posłużą do budowania wielomianu (tutaj jednomianu tzn. funkcji liniowej).
Ze względu na konieczność utrzymania symetrii okna tzn. dane w oknie powinny znajdować się powyżej i poniżej punktu, dla którego budujemy model, liczba elementów w oknie powinna być nieparzysta. Dlatego też uzyskana na podstawie parametru 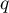 liczba elementów zaokrąglana jest w górę do pierwszej liczby nieparzystej. W ten sposób powstaje okno zawierające element
liczba elementów zaokrąglana jest w górę do pierwszej liczby nieparzystej. W ten sposób powstaje okno zawierające element 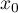 oraz odpowiednią liczbę
oraz odpowiednią liczbę 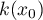 elementów znajdujących się przed tym elementem i za tym elementem w uporządkowanym zbierze danych.
elementów znajdujących się przed tym elementem i za tym elementem w uporządkowanym zbierze danych.
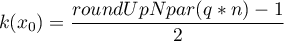
Przykładowo, gdy w oknie ma się znaleźć 7 elementów, to znajdzie się w nim element 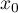 oraz trzy wcześniejsze i trzy późniejsze elementy próby. Okno wyznaczone dla pierwszych i ostatnich elementów próby jest tej samej wielkości, ale badany element nie jest w nim umieszczony symetrycznie tzn. na środku.
oraz trzy wcześniejsze i trzy późniejsze elementy próby. Okno wyznaczone dla pierwszych i ostatnich elementów próby jest tej samej wielkości, ale badany element nie jest w nim umieszczony symetrycznie tzn. na środku.
(2)
W każdym punkcie zbioru danych dopasowany jest wielomian niskiego stopnia (tutaj funkcja liniowa) do podzbioru zlokalizowanych w oknie danych. Dopasowanie dokonywane jest przy użyciu ważonej metody najmniejszych kwadratów, co daje większą wagę punktom w pobliżu punktu, którego odpowiedź jest szacowana, i mniejszą wagę punktom oddalonym. W ten sposób do każdego punktu przypisana jest inna formuła funkcji wielomianu (tutaj funkcji liniowej).
Stosowane w ważonej metodzie najmniejszych kwadratów wagi mogą być ustawiane dość elastycznie, ale punkty odległe od zadanego muszą mieć mniejszą wagę niż punkty w pobliżu. Tutaj posłużono się wagami zaproponowanymi przez Clevelanda tzw. tricube
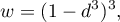 gdzie odległość
gdzie odległość 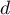 od punku
od punku 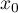 wyniosła 0 -dla punktów znajdujących się poza wyznaczonym oknem i była podana jako rzeczywista odległość między punktami, ale znormalizowana do przedziału [0,1] -dla punktów zlokalizowanych w oknie, tak by maksymalne odległości we wszystkich oknach były takie same.
wyniosła 0 -dla punktów znajdujących się poza wyznaczonym oknem i była podana jako rzeczywista odległość między punktami, ale znormalizowana do przedziału [0,1] -dla punktów zlokalizowanych w oknie, tak by maksymalne odległości we wszystkich oknach były takie same.
(3)
W każdym punkcie, na podstawie przypisanej do niego formuły wielomianu (tutaj funkcji liniowej) obliczana jest wartość funkcji 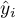 . Na podstawie punktów
. Na podstawie punktów  oraz estymowanych tą metodą punktów
oraz estymowanych tą metodą punktów 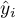 wyrysowywana jest wygładzona i dopasowana do danych funkcja.
wyrysowywana jest wygładzona i dopasowana do danych funkcja.
Wygładzanie jądrowe
Oszacowanie funkcji regresji metodą wygładzania jądrowego jest czasem nazywane oszacowaniem Nadaraya-Watson (Nadaraya, 19644); Watson, 19645)). Szacowanie jądra jest średnią ważoną obserwacji w oknie wygładzania:
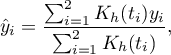
gdzie 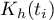 jest funkcją jądra opisaną w rozdziale Estymacja jądrowa.
jest funkcją jądra opisaną w rozdziale Estymacja jądrowa.
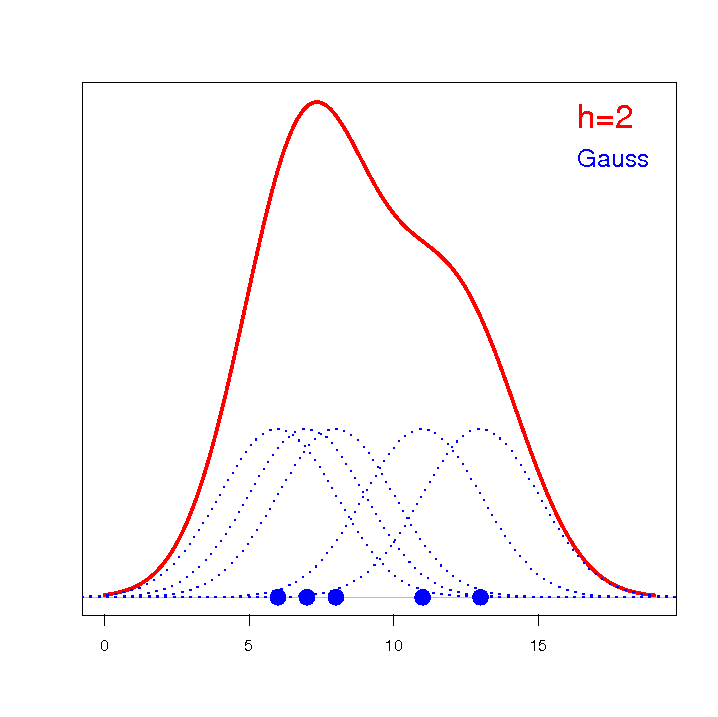
Parametr wygładzania 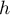 (ang. bandwidth) ma decydujący wpływ na uzyskany estymator. Im wyższa wartość parametru wygładzania, tym stopień wygładzenia jest większy. Do wyboru mamy możliwość dowolnego wyboru parametru wygładzania poprzez ustawienie wartości użytkownika. Możliwy jest również automatyczny dobór tej wielkości poprzez metodę SNR, SROT lub OS. Znacznie mniejszy wpływ na uzyskany wynik ma funkcja jądra. Do wyboru mamy jądro: Gaussa, w postaci funkcji jednostajnej (prostokąt), trójkątnej, Epanechnikova, quartic lub biweight (czwartego stopnia). Opis poszczególnych wielkości parametru wygładzania i funkcji jądra można znaleźć we wspomnianym rozdziale.
(ang. bandwidth) ma decydujący wpływ na uzyskany estymator. Im wyższa wartość parametru wygładzania, tym stopień wygładzenia jest większy. Do wyboru mamy możliwość dowolnego wyboru parametru wygładzania poprzez ustawienie wartości użytkownika. Możliwy jest również automatyczny dobór tej wielkości poprzez metodę SNR, SROT lub OS. Znacznie mniejszy wpływ na uzyskany wynik ma funkcja jądra. Do wyboru mamy jądro: Gaussa, w postaci funkcji jednostajnej (prostokąt), trójkątnej, Epanechnikova, quartic lub biweight (czwartego stopnia). Opis poszczególnych wielkości parametru wygładzania i funkcji jądra można znaleźć we wspomnianym rozdziale.
Okno z ustawieniami opcji wykresu punktowego z dopasowaną funkcją metodą LOWESS lub poprzez wygładzanie jądrowe znajdziemy w różnych analizach. Wykres ten możemy również wykonać poprzez menu Wykresy→Wykres punktowy.
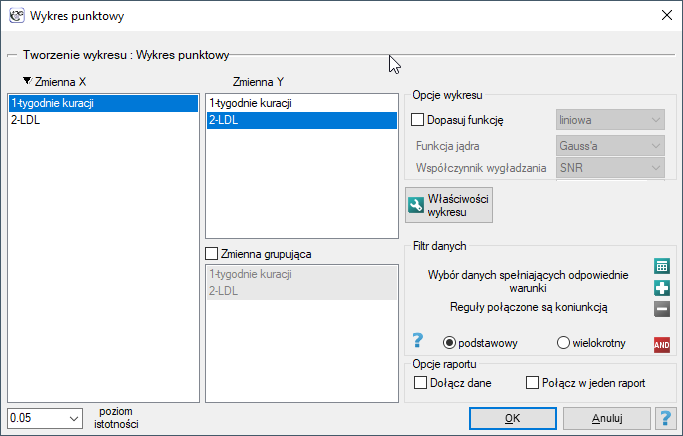
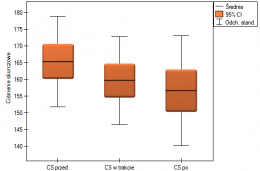
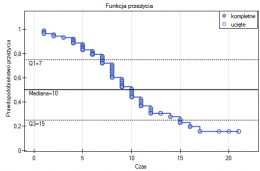
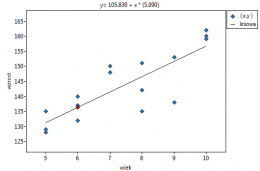
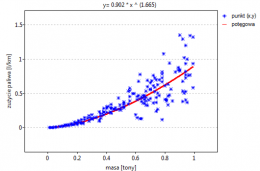
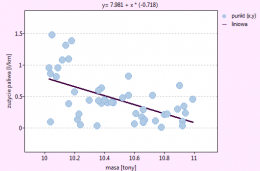
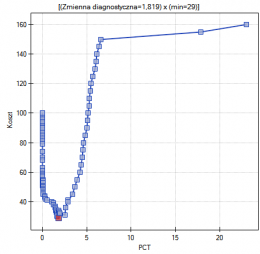
Przykład c.d. (plik LDL tygodnie.pqs)
Badano skuteczność nowej terapii, której celem jest obniżenie poziomu cholesterolu we frakcji LDL. Przebadano 88 osób na różnym etapie kuracji. Sprawdzimy, czy wraz z upływem czasu stosowania kuracji (czas w tygodniach) poziom cholesterolu LDL spada i się stabilizuje.
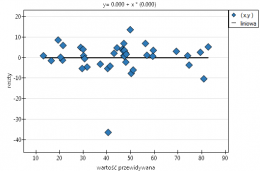
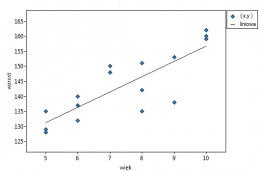
Wyniki przedstawiono początkowo dopasowując linię prostą wskazującą kierunek badanej zależności.
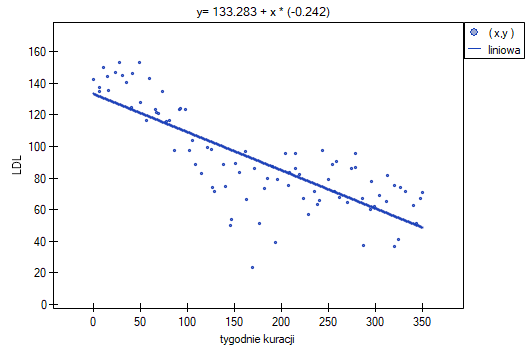
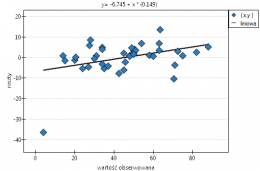
Jednak ten sposób przedstawienia danych nie oddaje w pełni zachodzących zależności. Z ułożenia punktów można zauważyć, że zależność ta jest początkowo malejąca, a po 150 tygodniach zaczyna się stabilizować. Zależność przedstawiono ponownie korzystając z metody LOWESS oraz z wygładzania jądrowego Gaussa.
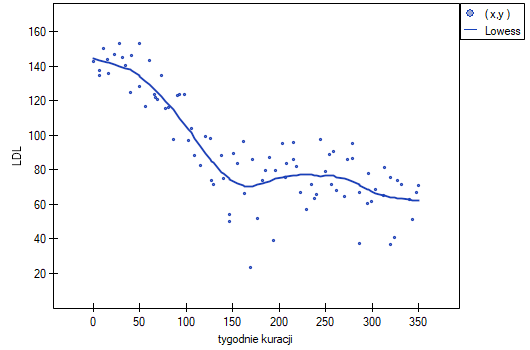
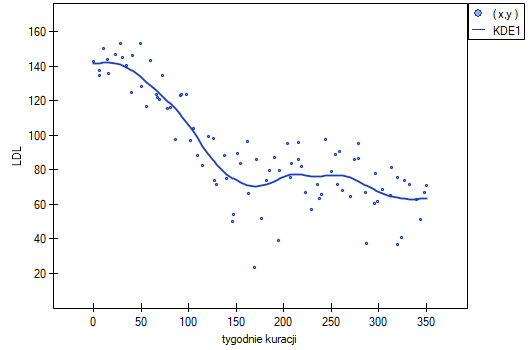
Obydwa sposoby tzn. zarówno LOWESS jak i wygładzanie jądrowe dały zbliżone wyniki i znacznie lepiej opisały dane, wskazując na początkowy spadek LDL a następnie jego stabilizację na poziomie bliskim 70 mg/dl.
Estymacja jądrowa
Jednowymiarowy estymator jądrowy
Jednowymiarowy jądrowy estymator gęstości pozwala na przybliżenie gęstości rozkładu danych tworząc wygładzoną krzywą gęstości w sposób nieparametryczny. Dzięki niemu uzyskuje się lepszą estymację gęstości niż daje tradycyjny histogram, którego kolumny tworzą funkcję schodkową.
Estymator jądrowy definiowany jest w oparciu o odpowiednio wygładzone jądro 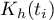 . Parametr wygładzania
. Parametr wygładzania 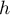 (ang. bandwidth) ma decydujący wpływ na uzyskany estymator. Im wyższa wartość parametru wygładzania, tym stopień wygładzenia jest większy.
(ang. bandwidth) ma decydujący wpływ na uzyskany estymator. Im wyższa wartość parametru wygładzania, tym stopień wygładzenia jest większy.
Dla każdego punktu 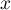 z zakresu określonego przez dane wyznacza się gęstość czyli podaje wartość estymatora jądrowego w tym punkcie. Estymator ten powstaje poprzez zsumowanie wartości funkcji jąder
z zakresu określonego przez dane wyznacza się gęstość czyli podaje wartość estymatora jądrowego w tym punkcie. Estymator ten powstaje poprzez zsumowanie wartości funkcji jąder 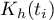 w tym punkcie:
w tym punkcie:
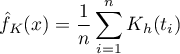
Jeśli poszczególnym przypadkom nadamy wagi 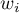 , wówczas możemy zbudować ważony jądrowy estymator gęstości definiowany wzorem:
, wówczas możemy zbudować ważony jądrowy estymator gęstości definiowany wzorem:
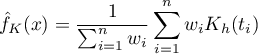
Współczynniki wygładzania
- Użytkownika - daje możliwość wybrania dowolnego współczynnika wygładzania wskazanego przez użytkownika, przy czym współczynnik ten musi być dodatni.
- Użytkownika skalowane - jest ustalane tak, by można było zmieniać funkcję jądra pozostając przy wygładzeniu jakie wybrane zostało wcześniej dla jądra Gaussa. W praktyce wybierając inną funkcję niż Gaussa współczynnik wygładzania zostaje przeskalowany (Scott, D. W. 19926)), przez co wygładzenie pozostaje na podobnym poziomie jaki był dla funkcji Gaussa. Daje to wygodę przełączania się pomiędzy różnymi jądrami bez rozważania skalowania parametru wygładzania. Przeliczenia dotyczące skalowania dokonywane są w oparciu o odchylenie standardowe:
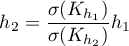
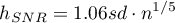
Dla jądra innego niż Gaussa, współczynnik wygładzania podlega skalowaniu (Scott D. W., 19929))
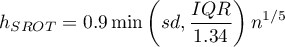
Dla jądra innego niż Gaussa, współczynnik wygładzania podlega skalowaniu (Scott D. W., 199212))
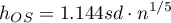
Dla jądra innego niż Gaussa, współczynnik wygładzania podlega skalowaniu (Scott D. W., 199215))
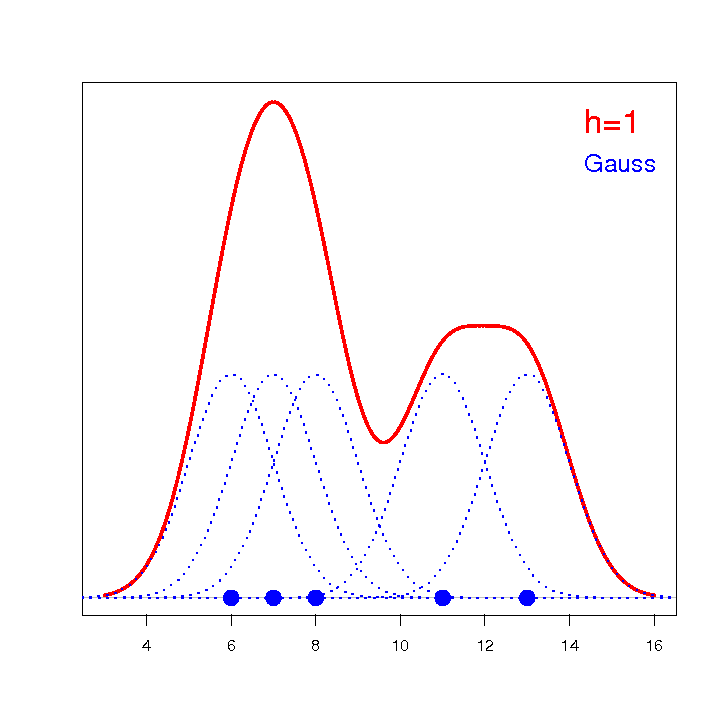
Funkcja jądra w mniejszym zakresie niż parametr wygładzania wpływa na uzyskaną wartość estymatora jądrowego. Jądro jest funkcją gęstości prawdopodobieństwa budowaną wokół każdego punktu danych  . Zwykle jest to funkcja symetryczna osiągająca maksimum w punkcie
. Zwykle jest to funkcja symetryczna osiągająca maksimum w punkcie  , a zmniejszająca swoje wartości wraz z oddalaniem się (wzrostem odległości
, a zmniejszająca swoje wartości wraz z oddalaniem się (wzrostem odległości 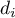 ) od tego punktu. Odległość od analizowanego punktu jest modyfikowana przez parametr wygładzania
) od tego punktu. Odległość od analizowanego punktu jest modyfikowana przez parametr wygładzania 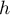 zgodnie z wzorem:
zgodnie z wzorem: 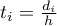 .
.
W zależności od potrzeb funkcja jądra może przyjmować postać funkcji:
- Gaussa
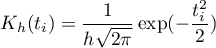
- jednostajnej (prostokąt)
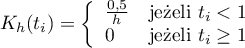
- trójkątnej
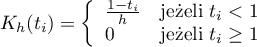
- Epanechnikova
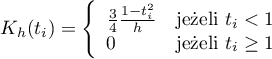
- quartic lub biweight (czwartego stopnia)
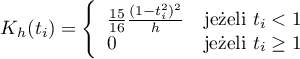
![LaTeX
\textcolor{green}{Gaussa}
\textcolor{red}{jednostajna}
\textcolor{blue}{trójkątna}
\textcolor{orange}{Epanechnikova}
\textcolor[rgb]{0,0.58,0}{quartic/biweight}](/lib/exe/fetch.php?media=wiki:latex:/imgef368a2a394bf425fa6fccb67382004e.png)
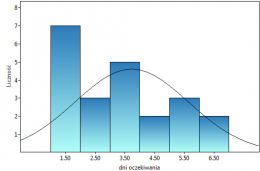
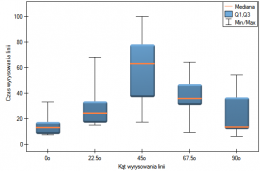
Przykład (plik BMI.pqs)
Wyliczono wartości współczynnika wagowo-wzrostowego BMI1 dla pewnej grupy osób otyłych. Przedstawiono ich rozkład za pomocą histogramu z podziałem wartości co 1 jednostkę BMI. Dane zobrazowano również za pomocą jądrowego estymatora gęstości wybierając Gaussowską funkcję jądra i ustawiając współczynniki wygładzania odpowiednio: 0.5, 1, 2.
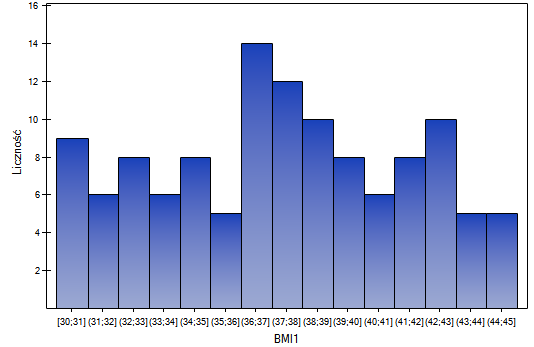
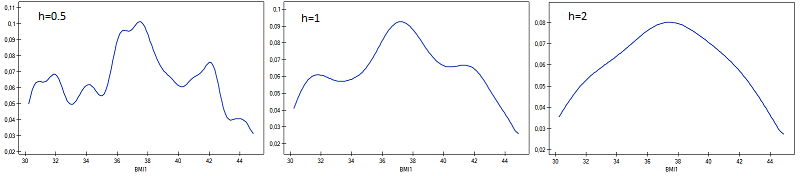
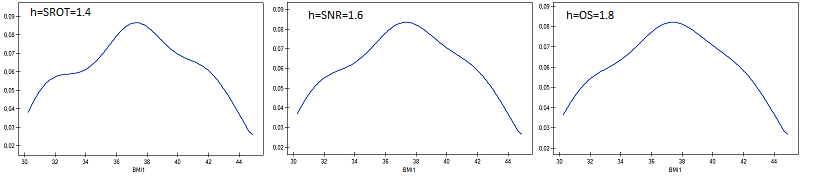
Współczynniki wygładzania estymatora jądrowego sugerowane przez metody SROT, SNR i OS osiągają wielkości pomiędzy 1.4 a 2.
Wykres Blanda-Altmana
Jak zauważył Bland i Altman (198616), 199917)) w medycynie klinicznej pomiary wykonywane na żywym organiźmie ulegają ciągłym zmianom a ich prawdziwa wartość jest nieznana (np. ciśnienie tętnicze krwi), co wymaga ciągłego doskonalenia i tworzenia nowych, lepszych narzędzi ich pomiaru. Zwykle, kiedy tworzona jest nowa metoda, porównuje się jej wyniki z inną, uznaną metodą tzw. gold standard. W tym celu bada się zgodność nowej metody z metodą dotychczas stosowaną. Oczywiście, nie można oczekiwać, że nowa metoda da dokładnie ten sam wynik co metoda dotychczas wykorzystywana, ale badaczowi zależy na sprawdzeniu na ile różnią się uzyskane wyniki. By zastąpić starą metodę metodą nową, uzyskana różnica pomiędzy wynikami obu metod powinna być na tyle mała, by nie stwarzać problemu w interpretacji klinicznej. Na przykład w pomiarach ciśnienia tętniczego krwi różnica wielkości 20mmHg będzie na tyle duża, że nie może zostać uznana za dozwolony błąd, ponieważ może rzutować na zmianę decyzji o podjęciu leczenia. Metody statystyczne nie odpowiedzą na pytanie jak duża różnica metod jest dozwolona, by można było uznać metody za zgodne, ale odpowiednia ilustracja graficzna uzyskanych różnic i możliwych granic zmienności ułatwi podjęcie decyzji badaczowi.
Wykres Blanda-Altmana jest wykresem punktowym, gdzie:
- Oś X - średnia pomiarów dla porównywanych metod;
- Oś Y - różnica pomiędzy pomiarami dla porównywanych metod;
- Średnia różnic - jeśli wyniki uzyskane nową metodą są stale większe/mniejsze niż metodą starą, wówczas występuje przesunięcie, które nazywamy ang. bias, czyli linia obrazująca średnią różnic nie znajduje się na poziomie 0, ale jest przesunięta znacząco w górę lub w dół od tego poziomu.
- 95% przedział zgodności - jeśli różnice mają rozkład normalny, 95% różnic znajdzie się w przedziale (Średnia różnic
 1.96SD), gdzie SD, to odchylenie standardowe różnic.
1.96SD), gdzie SD, to odchylenie standardowe różnic.
Uwaga1! Zdefiniowany powyżej przedział zgodności nie jest tym samym co przedział ufności.
Uwaga2! Nie ma wymogu, by dane miały rozkład normalny a jedynie by rozkład różnic nie odbiegał znacznie od rozkładu normalnego. Możemy sprawdzić czy różnice mają rozkład normalny korzystając z testów badających zgodność z rozkładem normalnym lub interpretacji graficznej tego rozkładu.
- Precyzja granic przedziału zgodności - jest to przedział ufności dla granic, a więc przedział dokładności z jaką wyznaczamy granice bazując na reprezentatywnej próbie. Czym liczniejsza będzie próba i czym mniejsza będzie wariancja różnic, tym uzyskana precyzja będzie większa.
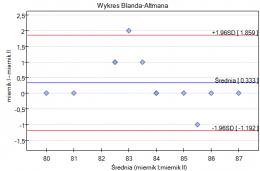
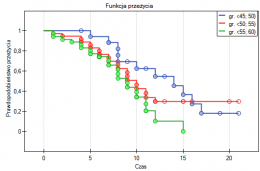
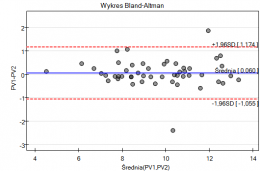
Przykład (plik ciśnieniomierz.pqs)
Przykład został zaczerpnięty z pracy Blanda i Altmana (199918)). Porównano w niej ciśnieniomierz półautomatyczny (S) z tradycyjnie stosowanym wcześniej klasycznym ciśnieniomierzem (J). W tym celu dokonano pomiaru ciśnienia skurczowego krwi dla 85 pacjentów przy pomocy obu ciśnieniomierzy. Fragment danych przedstawiono poniżej.
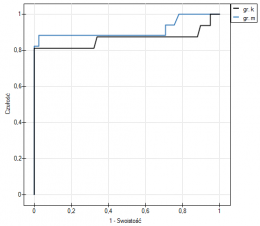
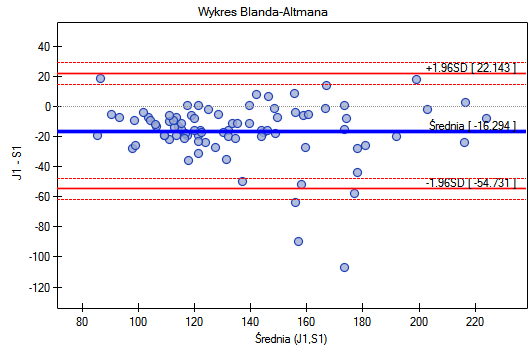
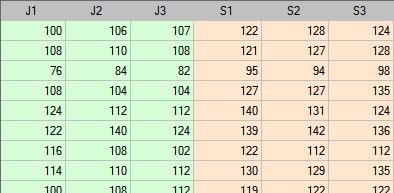
Wykres Blanda-Altmana dla zebranych danych wskazuje, że ciśnieniomierz półautomatyczny (S) daje wyższe wyniki niż klasyczny średnio o 16.3mmHG (linia dla średniej różnic znajduje się o 16.3 niżej niż bezwzględna zgodność zobrazowana linią poziomie 0). Rozpiętość przedziału zgodności wynosi aż 76.9mmHG.
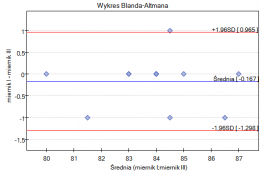
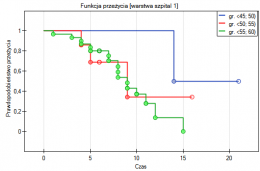
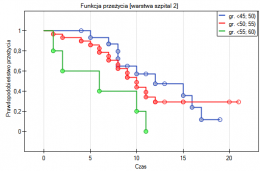
Dla osób z nadciśnieniem (ciśnienie skurczowe 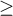 140) zmiany ciśnienia mogą być dość duże, więc badane różnice pomiarów mogą być zaburzone przez rzeczywiste skoki ciśnienia, dlatego wyodrębniono podgrupę osób z ciśnieniem w normie i nadciśnieniem na podstawie średniej wartości ciśnienia. Dla każdej podgrupy możemy wykonać wykres oddzielnie ustawiając w oknie testu filtr wielokrotny dla zmiennej grupa. Zgodność metod dla osób z ciśnieniem w normie będzie wówczas zdecydowanie lepsza (węższy przedział zgodności).
140) zmiany ciśnienia mogą być dość duże, więc badane różnice pomiarów mogą być zaburzone przez rzeczywiste skoki ciśnienia, dlatego wyodrębniono podgrupę osób z ciśnieniem w normie i nadciśnieniem na podstawie średniej wartości ciśnienia. Dla każdej podgrupy możemy wykonać wykres oddzielnie ustawiając w oknie testu filtr wielokrotny dla zmiennej grupa. Zgodność metod dla osób z ciśnieniem w normie będzie wówczas zdecydowanie lepsza (węższy przedział zgodności).
Wykres Blanda-Altmana dla powtarzanych pomiarów
Powtarzalność pomiarów jest ważnym, lecz często pomijanym aspektem w badaniu zgodności metod. Metoda o większej powtarzalności jest bardziej precyzyjna. Jeśli pomiary jednej z porównywanych metod nie są powtarzalne (tzn. powtórne pomiary wykonane na tych samych obiektach dają raczej inne wyniki), jej zgodność z inną metodą będzie niska. Jeśli powtarzalność obu metod będzie słaba, to ich zgodność będzie jeszcze niższa. W konsekwencji, gdy powtarzalność starej metody będzie słaba, zgodność nowej metody może okazać się niewielka, nawet jeśli nowa metoda charakteryzuje się wysoką powtarzalnością. Dlatego, mimo że w rzeczywistych badaniach wykonuje się jeden pomiar dla każdego obiektu (pacjenta), w badaniach mających na celu szacowanie zgodności zaleca się wykonywanie pomiarów kilkukrotnie. Takie podejście daje możliwość uwzględnienia powtarzalności uzyskanych wyników w badaniach nad zgodnością metod.
Uwaga! Jako powtarzane pomiary rozumiemy tutaj pomiary wykonywane niezależnie na tych samych obiektach, w takich samych warunkach.
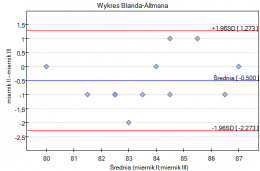
Przykład c.d. (plik plik ciśnieniomierz.pqs)
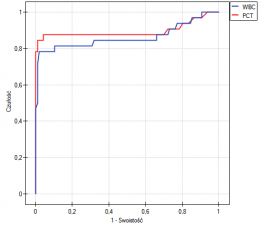
W porównaniu zgodność pomiarów dokonanych przy pomocy porównywanych ciśnieniomierzy wzięto pod uwagę również powtarzalność obu metod. Dlatego badanie powtórzono jeszcze dwukrotnie uzyskując ostatecznie dla każdego pacjenta 3 pomiary wykonane przy pomocy ciśnieniomierza półautomatycznego i 3 pomiary wykonane przy pomocy ciśnieniomierza klasycznego. Fragment danych przedstawiono poniżej.
Tym razem granice zgodności są nieco szersze niż przy wykorzystaniu pojedynczego pomiaru dla każdej metody - rozpiętość przedziału zgodności wynosi aż 82.11mmHG. Dzieje się tak dlatego, że uwzględniamy stopień powtarzalności pomiarów. Niestety, uwzględnienie kilku powtórzeń zwiększa szerokość granic, ale przedstawione wyniki lepiej reprezentują rzeczywistość. Nie uwzględniając bowiem stopnia powtarzalności zakładamy, że powtarzalność jest 100 procentowa, co w rzeczywistych warunkach jest niemal niemożliwe.
Podobnie jak poprzednio, zaleca się powtórzyć analizę oddzielnie dla osób z nadciśnieniem i z ciśnieniem w normie.
Macierze korelacji
Kiedy interesuje nas korelacja pomiędzy wieloma zmiennymi, wygodnym sposobem jej zobrazowania jest przedstawienie współczynników korelacji w postaci tabeli. W zależności od skali na jakiej zebrano dane, w programie PQStat mamy do wyboru współczynniki:
- r-Pearsona (skala interwałowa)
- r-Spearmana (skala porządkowa lub silniejsza)
- tau-Kendalla (skala porządkowa lub silniejsza)
- C-Pearsona (skala nominalna lub silniejsza)
- V-Cramera (skala nominalna lub silniejsza)
- Phi (skala nominalna lub silniejsza)
- Q-Yulea (skala nominalna lub silniejsza)
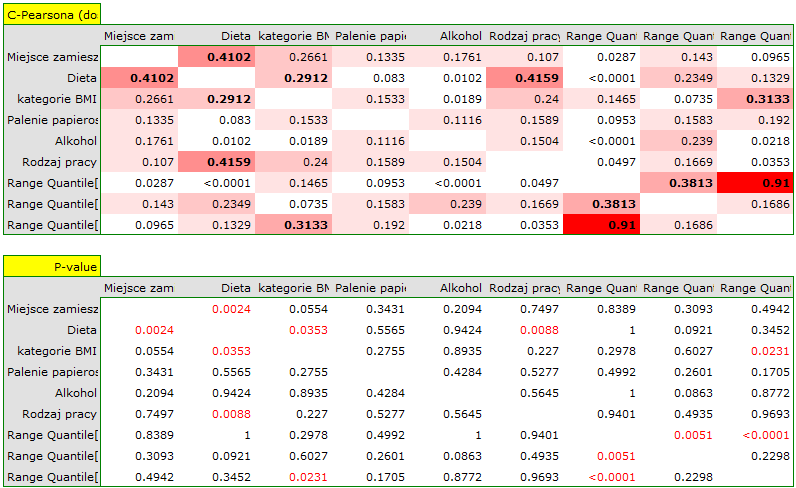
W wyniku analizy powstają dwie macierze, tzn. macierz współczynników korelacji i macierz wartości p dla testu określającego istotność statystyczną danego współczynnika (dla włóczników r-Pearsona, r-Pearsona i tau-Kendalla były to dedykowane im testy, dla skali nominalnej test chi-kwadrat). W macierzy współczynników korelacji , w miejscu przecięcia się dwóch zmiennych podany jest współczynnik ich korelacji, a jego wartość p znajduje się w odpowiadającym mu miejscu w drugiej macierzy. Kolor komórki w macierzy współczynników jest stopniowany od niebieskiego (ujemne współczynniki) do czerwonego (dodatnie współczynniki).
Analiza wyznacza korelację dla każdej pary zmiennych, dlatego braki danych pomijane są parami. Jeśli chcemy przeprowadzić analizę pomijając barki danych występujące w innych zmiennych (tzn. nie tych, które wchodzą w skald danej pary), wówczas powinniśmy to zrobić korzystając z filtru zaawansowanego.
Okno z ustawieniami opcji macierzy korelacji wywołujemy poprzez Statystyki→Kalkulatory→Macierze korelacji
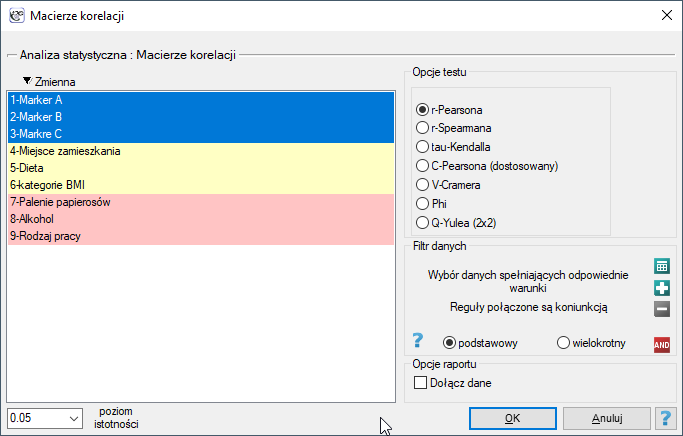
Okno z ustawieniami opcji wykresu macierzowego dla macierzy korelacji wywołujemy poprzez Wykresy→Wykres macierzowy
Przykład (plik markery inne.pqs)
Przedstawiono fragment większego badania dotyczącego choroby nowotworowej. Zabrane dane dotyczą grupy 100 osób. W badaniu mierzono min. wartości markerów nowotworowych (skala interwałowa), wyznaczono kategorie BMI dla pacjentów oraz pytano o opinie na temat możliwego wpływu miejsca zamieszkana oraz diety na zdrowie (skala porządkowa), zanotowano też odpowiedzi pacjentów na temat palenia przez nich papierosów, spożywania alkoholu oraz rodzaju wykonywanej pracy (skala nominalna).
Prowadzenie analiz wielowymiarowych często zakłada konieczność wcześniejszego sprawdzenia wzajemnych korelacji zmiennych. Na potrzeby dalszych analiz:
(1) Sprawdzimy korelację wewnątrz każdej z tych grup.
(2) Sprawdzimy korelację między wszystkimi zmiennymi.
(1)
Dla skali interwałowej, przy założeniu normalności rozkładu korelację możemy sprawdzić współczynnikiem korelacji liniowej Pearsona. Najsilniejsza korelacja dotyczy markera A i markera C (r=0.8995, p<0.0001) najsłabsza i nieistotna statystycznie dotyczy markera B i markera C (r=0.0753, p=0.4567).
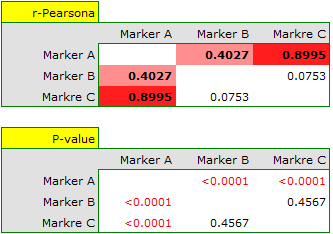
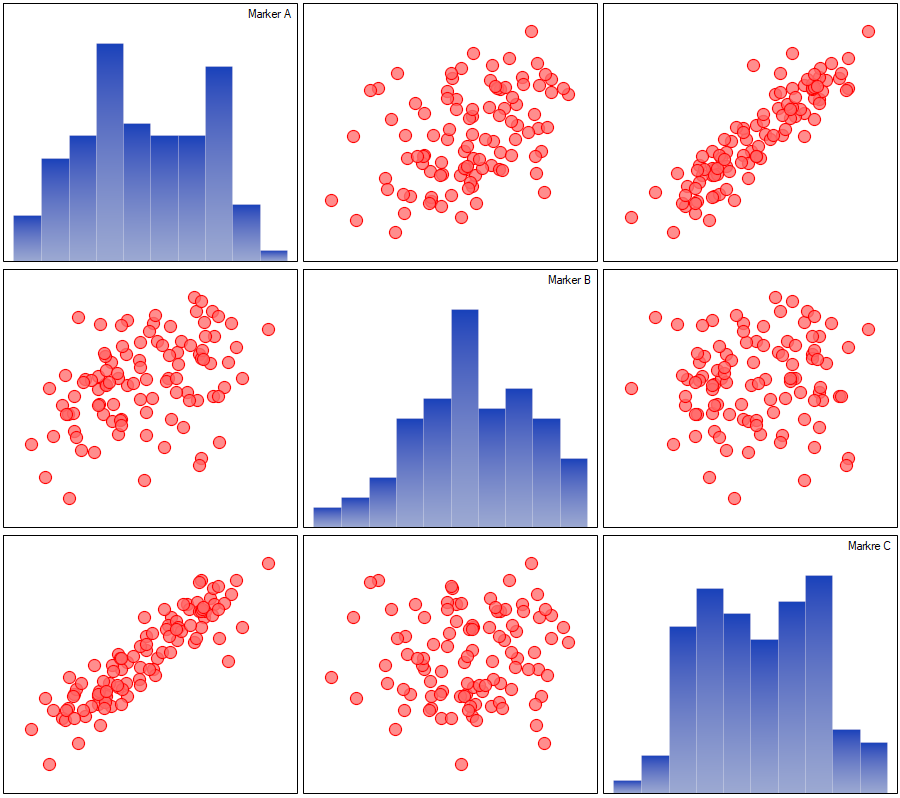
Opisane korelacje można obserwować na wykresach rozrzutu (oś X tych wykresów to zmienna opisana w kolumnach, oś Y w wierszach), a rozkłady poszczególnych zmiennych na wykresach kolumnowych.
Dla skali porządkowej korelację sprawdzimy przy pomocy współczynnika korelacji Spearmana. Jedyna istotna korelacja dotyczy diety i miejsca zamieszkania (r=0.2634, p=0.0081)
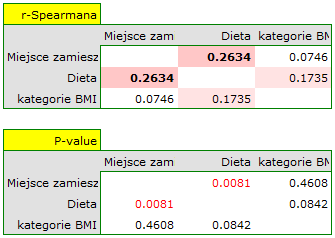
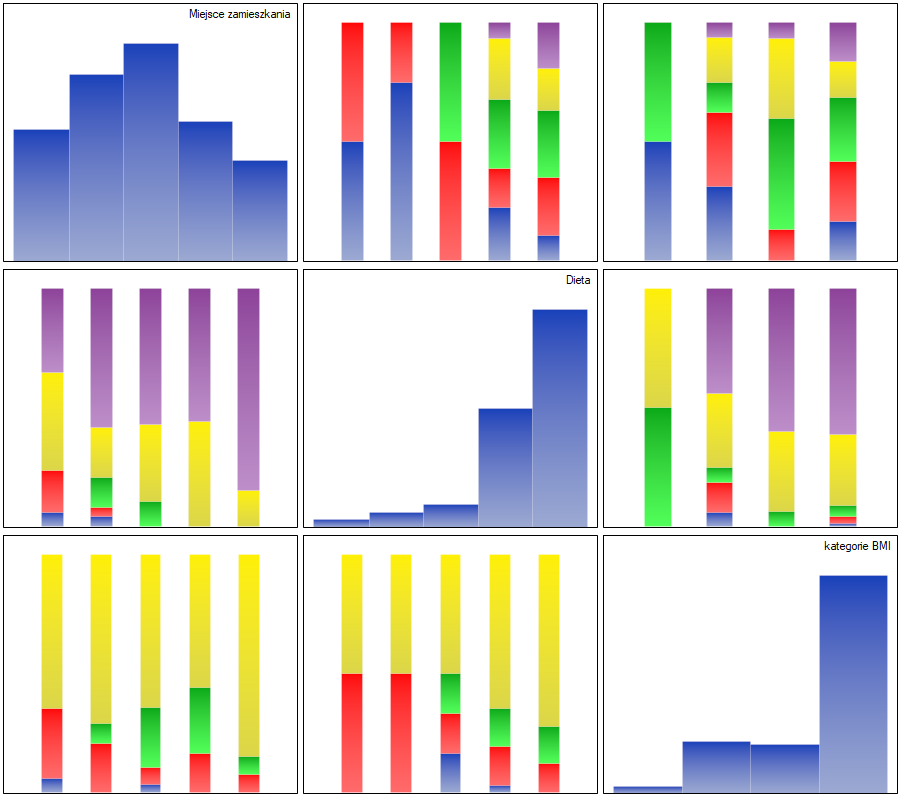
Opisane korelacje można obserwować na wykresach kolumnowych skumulowanych (oś X tych wykresów to zmienna opisana w kolumnach, legenda to zmienna opisana w wierszach), a rozkłady poszczególnych zmiennych na wykresach kolumnowych znajdujących się na głównej przekątnej.
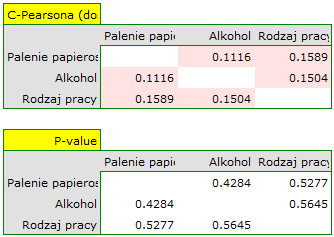
Dla skali nominalnej korelację sprawdzimy przy pomocy współczynnika C-Pearsona skorygowanego na wielkość tabeli. Nie uzyskaliśmy istotnych statystycznie korelacji.
Ewentualne korelacje można obserwować na wykresach kolumnowych skumulowanych (oś X tych wykresów to zmienna opisana w kolumnach, legenda to zmienna opisana w wierszach), a rozkłady poszczególnych zmiennych na wykresach kolumnowych znajdujących się na głównej przekątnej.
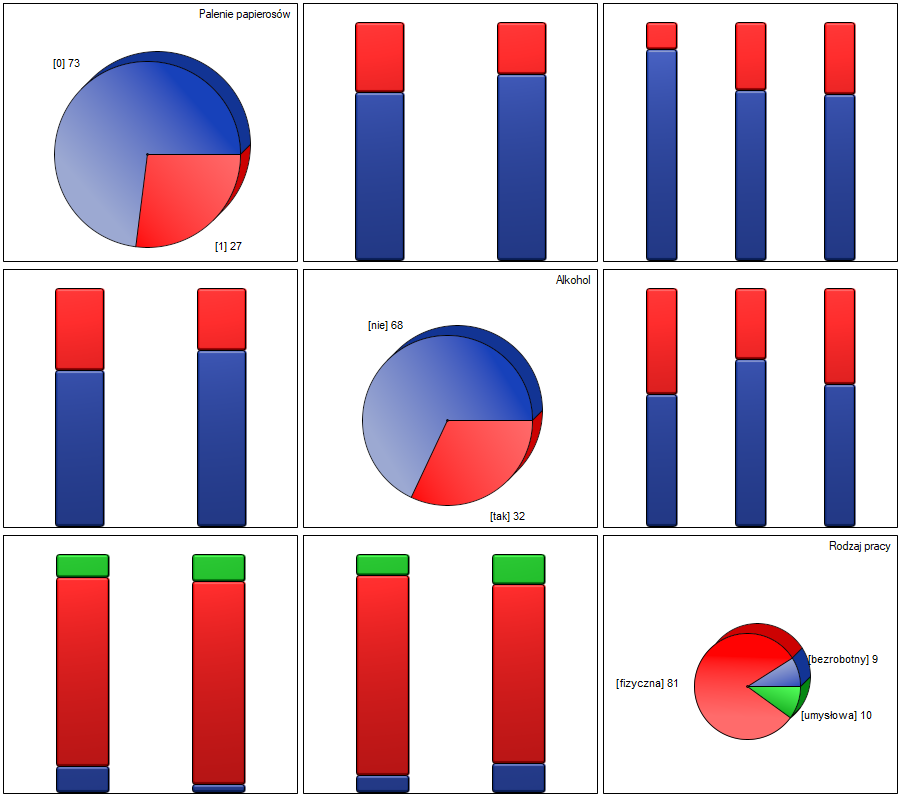
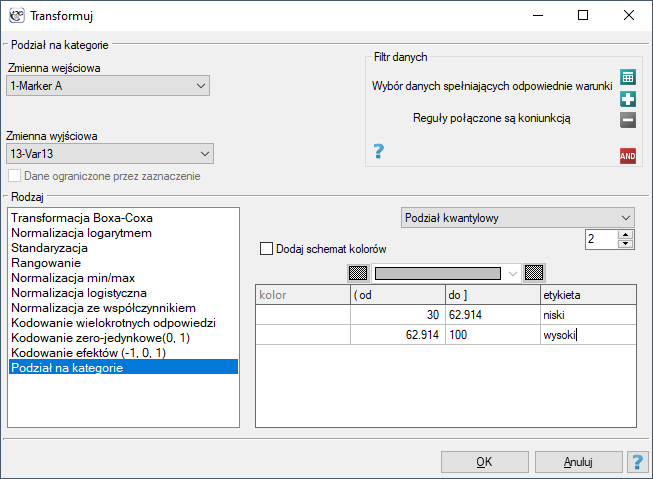
(2) Najłatwiejszym sposobem wyznaczania korelacji pomiędzy zmiennymi mierzonymi na różnych skalach jest sprowadzenie ich do tej samej skali. W tym celu zapiszemy dane interwałowe dzieląc je na dwie kategorie niski i wysoki np. wg kwantyli. Możemy to z robić automatycznie w oknie transformacji poprzez menu Dane→Transformuj.
Dane iporządkowe również podzielimy na dwie kategorie, ale podziału dokonamy wybierając Właściwości zmiennych (kody/etykiety) w oknie analizy poprzez menu kontekstowe (prawy klawisz myszy) i wpisując tylko dwie obowiązujące wartości i dwie etykiety.
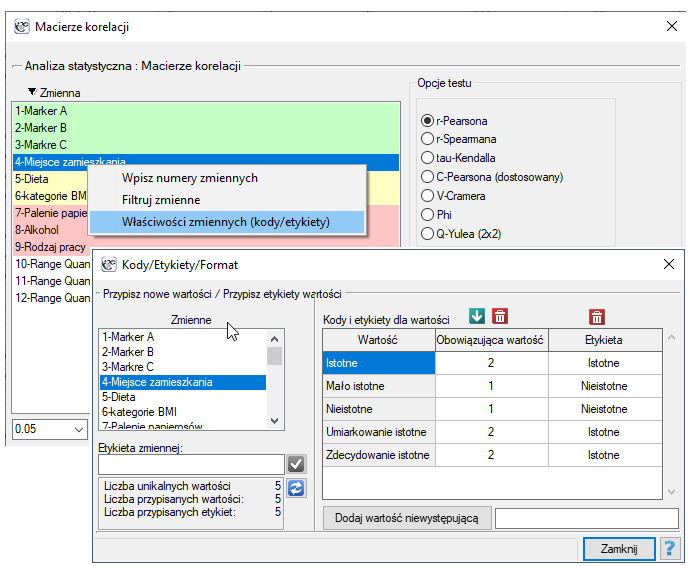
W wyniku przedstawimy tylko macierz korelacji (bez wykresu), ponieważ wykres dla tak wielu zmiennych nie będzie wystarczająco czytelny.