Współczynnik zgodności Kendalla i test badający jego istotność
Współczynnik zgodności 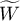 Kendalla (ang. Kendall's Coefficient of Concordance) opisany w pracy Kendalla i Babingtona-Smitha (1939)1) oraz Wallisa (1939)2) stosuje się w sytuacji, gdy dysponujemy rankingami pochodzącymi z różnych źródeł (od różnych sędziów) i dotyczącymi kilku (
Kendalla (ang. Kendall's Coefficient of Concordance) opisany w pracy Kendalla i Babingtona-Smitha (1939)1) oraz Wallisa (1939)2) stosuje się w sytuacji, gdy dysponujemy rankingami pochodzącymi z różnych źródeł (od różnych sędziów) i dotyczącymi kilku (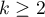 ) obiektów a zależy nam na ocenie zgodności tych rankingów. Często używa się go do mierzenia siły sędziowskiej rzetelności, czyli stopnia w jakim oceny sędziów są zgodne.
) obiektów a zależy nam na ocenie zgodności tych rankingów. Często używa się go do mierzenia siły sędziowskiej rzetelności, czyli stopnia w jakim oceny sędziów są zgodne.
Współczynnik zgodności Kendalla wyznacza się dla skali porządkowej lub interwałowej, a jego wartość wylicza się według wzoru:
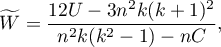
gdzie:
 - liczba różnych zbiorów ocen (ilość sędziów),
- liczba różnych zbiorów ocen (ilość sędziów),
 - liczba rangowanych obiektów,
- liczba rangowanych obiektów,
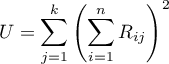 ,
,
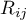 - rangi przypisane kolejnym obiektom
- rangi przypisane kolejnym obiektom  , oddzielnie dla każdego z sędziów
, oddzielnie dla każdego z sędziów 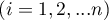 ,
,
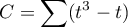 - korekta na rangi wiązane,
- korekta na rangi wiązane,
 - liczba przypadków wchodzących w skład rangi wiązanej.
- liczba przypadków wchodzących w skład rangi wiązanej.
Wzór na współczynnik zawiera poprawkę na rangi wiązane  . Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas
. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych poprawka ta nie jest wyliczana, gdyż wówczas 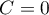 ).
).
Uwaga!
 oznacza współczynnik zgodności Kendalla w populacji, natomiast
oznacza współczynnik zgodności Kendalla w populacji, natomiast 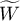 w próbie.
w próbie.
Wartość 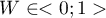 interpretujemy w następujący sposób:
interpretujemy w następujący sposób:
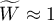 oznacza silną zgodność w ocenie poszczególnych obiektów przez sędziów;
oznacza silną zgodność w ocenie poszczególnych obiektów przez sędziów;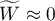 oznacza brak zgodności w ocenie poszczególnych obiektów przez sędziów.
oznacza brak zgodności w ocenie poszczególnych obiektów przez sędziów.
Współczynnik zgodności 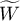 Kendalla a współczynnik
Kendalla a współczynnik 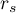 Spearmana:
Spearmana:
- Gdy wyliczymy wartość współczynnika korelacji Spearmana
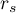 dla wszystkich możliwych par rankingów, to średni współczynnik
dla wszystkich możliwych par rankingów, to średni współczynnik 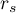 - oznaczony przez
- oznaczony przez 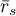 , jest funkcją liniową wartości współczynnika
, jest funkcją liniową wartości współczynnika 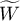 wyliczonego na podstawie tych danych:
wyliczonego na podstawie tych danych:
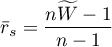
Współczynnik zgodności 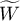 Kendalla a ANOVA Friedmana:
Kendalla a ANOVA Friedmana:
- Współczynnik zgodności
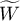 Kendalla i ANOVA Friedmana bazują na tym samym modelu matematycznym. W rezultacie wartość statystyki testowej testu chi-kwadrat do sprawdzania istotności współczynnika zgodności Kendalla i wartość statystyki testowej ANOVA Friedmana jest taka sama.
Kendalla i ANOVA Friedmana bazują na tym samym modelu matematycznym. W rezultacie wartość statystyki testowej testu chi-kwadrat do sprawdzania istotności współczynnika zgodności Kendalla i wartość statystyki testowej ANOVA Friedmana jest taka sama.
Test chi-kwadrat do sprawdzania istotności współczynnika zgodności Kendalla
Podstawowe warunki stosowania:
- pomiar na skali porządkowej lub interwałowej.
Hipotezy:
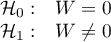
Statystyka testowa ma postać:
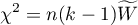
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyliczaną z wzoru: 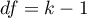 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji testu istotności W Kendalla wywołujemy poprzez menu Statystyka→Testy nieparametryczne→W Kendalla lub poprzez ''Kreator''.
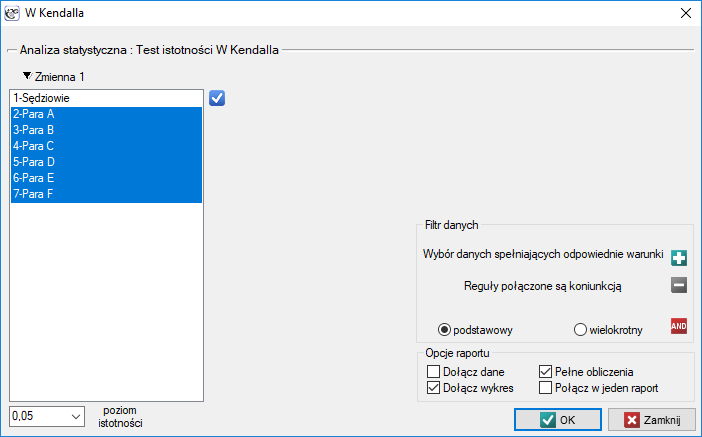
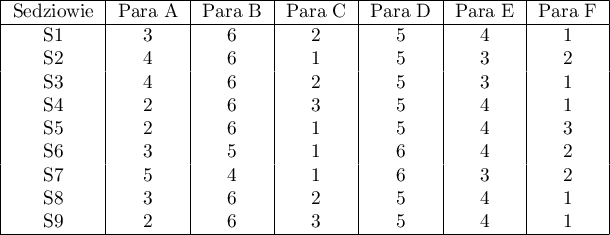
W systemie szóstkowym oceny par tanecznych 9 sędziów punktuje m.in. wrażenie artystyczne. Sędziowie rozpoczynają wystawianie oceny od porównania zawodników względem siebie i ustawienia ich na określonym miejscu (tworzą ich ranking). Sprawdzimy, czy rangi przypisane przez sędziów są zgodne:
Hipotezy:

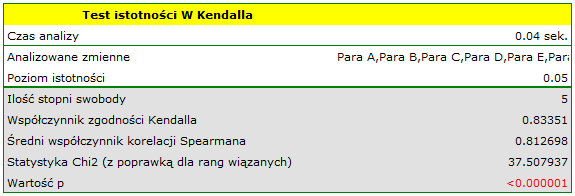
Porównując wartość 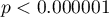 z poziomem istotności
z poziomem istotności  , stwierdziliśmy, że oceny sędziów są statystycznie zgodne. Siła tej zgodności jest wysoka i wynosi
, stwierdziliśmy, że oceny sędziów są statystycznie zgodne. Siła tej zgodności jest wysoka i wynosi 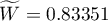 , podobnie jak średni współczynnik korelacji monotonicznej Spearmana
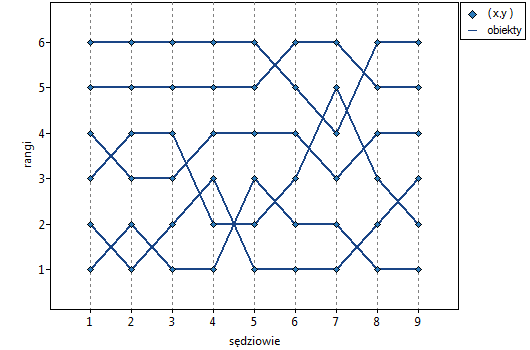
, podobnie jak średni współczynnik korelacji monotonicznej Spearmana 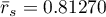 . Wynik ten możemy przedstawić na wykresie, na którym oś X reprezentuje kolejnych sędziów. Wówczas im częściej przecinają się linie, (które powinny być równoległe do osi X, gdy zgodność jest pełna), tym słabszą zgodność reprezentują oceny sędziów.
. Wynik ten możemy przedstawić na wykresie, na którym oś X reprezentuje kolejnych sędziów. Wówczas im częściej przecinają się linie, (które powinny być równoległe do osi X, gdy zgodność jest pełna), tym słabszą zgodność reprezentują oceny sędziów.