ANCOVA

Analiza kowariancji (ANCOVA) jest metodą testowania hipotezy o równości średnich dwóch lub większej liczby populacji, w korekcji o inne ciągłe zmienne. Skutkiem tych korekt są efekty chętniej widziane przez badaczy niż te uzyskiwane poprzez ANOVA, tzn. węższe przedziały ufności i większa moc statystyczna. Załóżmy, że przeprowadza się eksperyment w celu oceny efektów dwóch metod leczenia. Grupy, którym losowo przydzielono leczenie, różnią się nieco średnią wieku, która rówież wpływa na efekt leczenia. Różnice między grupami w osiągnięciach będą dość niejednoznaczne do zinterpretowania, ponieważ grupy różnią się zarówno pod względem wieku, jak i warunków leczenia. Analiza kowariancji dostarczy „skorygowanych średnich”, które szacują wartość, jaką miałyby średnie wyniki, gdyby grupy były dokładnie takie same pod względem wieku. Jednocześnie zmienność wyników w obrębie grupy, wynikająca ze zmiennej (wiek), zostanie usunięta ze zmienności błędu, aby zwiększyć precyzję testu różnic między skorygowanymi średnimi.
Oznaczenie „analiza kowariancji” jest obecnie postrzegane jako anachroniczne przez niektórych metodologów badań i statystyków, ponieważ analiza ta nie jest odrębną analizą ale wariantem ogólnego modelu liniowego (GLM). Jednak termin ten jest nadal użyteczny, ponieważ natychmiast przekazuje większości badaczy pojęcie, że zmienna kategorialna (np. warunki leczenia) i zmienna ciągła (np.wiek) są zaangażowane w jedną analizę określającą wynik leczenia.

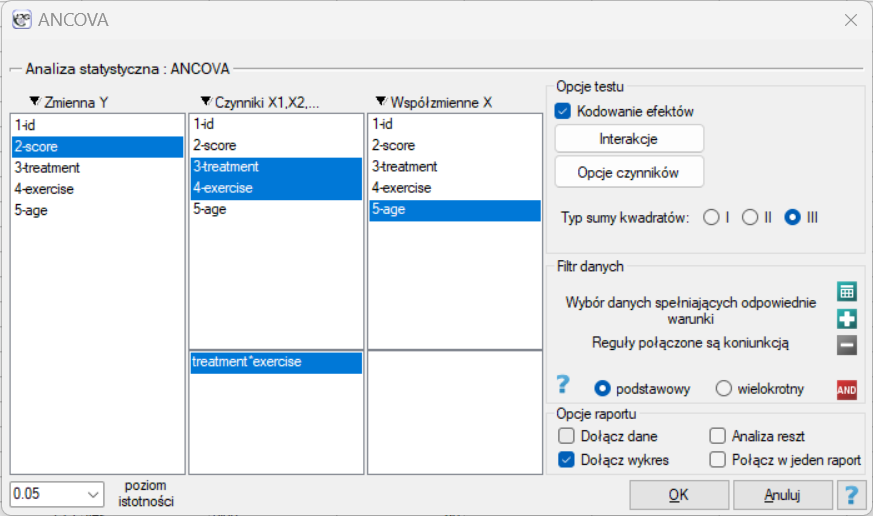
Okno z ustawieniami opcji ANCOVA wywołujemy poprzez menu Statystyka→Modele wielowymiarowe→ANCOVA

Uwaga!!!

Sposób uwzględniania badanych czynników i zmiennych wikłających opisany jest w rozdziale dotyczącym wieloczynnikowej ANOVA (Wpływ czynników wikłających). Polecanym sposobem jest wybór Sumy kwadratów typu III oraz kodowania efektów

Podstawowe warunki stosowania:

Uwaga!

Równość nachyleń linii regresji badana jest przy pomocy testu F porównującego model zawierający analizowane czynniki z takim samym modelem, ale powiększonym o interakcje z czynnikami wikłającymi. Istotny statystycznie wynik oznacza złamanie założenia równych nachyleń, ponieważ istotna staje się interakcja, a więc różne nachylenia prostych.

Hipotezy ANCOVA dla pojedynczego czynnika $A$:

\begin{array}{cl} \mathcal{H}_0: & \mu_1=\mu_2=...=\mu_a,\\ \mathcal{H}_1: & $nie wszystkie $\mu_i$ są sobie równe $(i=1,2,...,a), \end{array}

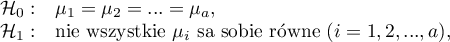
gdzie:

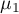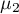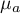$\mu_1$,$\mu_2$,…,$\mu_a$ - oczekiwane średnie czynnika $A$ dla poszczególnych jego kategorii.

Hipotezy ANCOVA dla interakcji czynników $A*B$:

\begin{array}{cl} \mathcal{H}_0: & \mu_1=\mu_2=...=\mu_{ab},\\ \mathcal{H}_1: & $nie wszystkie $\mu_k$ są sobie równe $(k=1,2,...,ab), \end{array}

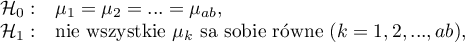
gdzie:

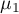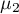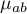$\mu_1$,$\mu_2$,…,$\mu_{ab}$ - oczekiwane średnie interakcji czynników $A*B$ dla poszczególnych ich kategorii.

Przykład (plik lekCholesterol.pqs)

Wyobraźmy sobie, że badacz prowadził badanie nad nowym lekiem obniżającym poziom cholesterolu. Badanie było tak zaprojektowane, że dawka leku występowała na trzech poziomach: wysoka, niska i placebo. Badacz sprawdził (przy pomocy ANOVA niezależna) czy cholesterol po leczeniu różnił się w zależności od dawki leku.

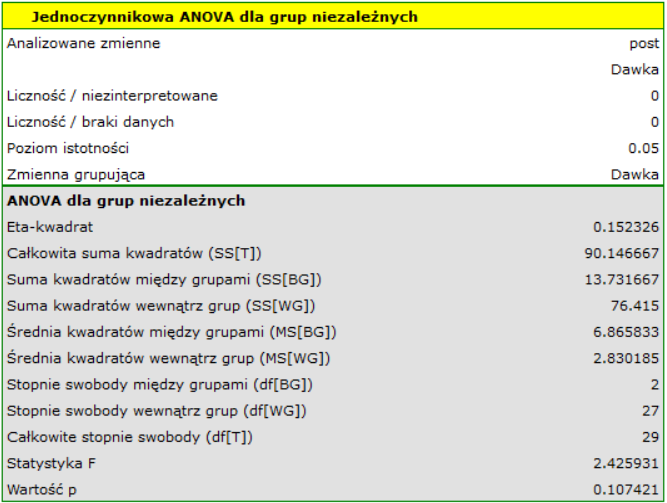
Niestety badacz nie uzyskł potwierdzenia różnic pomiędzy wynikami.

Wyobraźmy sobie, że badacz, zdał sobie sprawę, że to, czy dany lek zmieni poziom cholesterolu może być związane z wyjściowym poziomem cholesterolu oraz z wiekiem pacjenta. Z tego względu zdecydował się wykonać jednoczynnikową ANCOVA (czynnik to dawka leku) uwzględniającą jako współzmienną poziom cholesterolu przed leczeniem i wiek.

Tym razem wynik ANOCVA wskazał na występowanie istotnych różnic pomiędzy poziomem cholesterolu po zastosowaniu różnych dawek leku (p=0.00003):

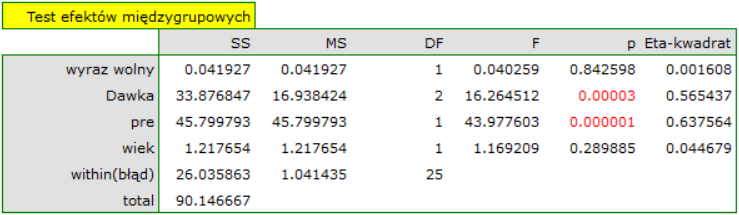
Uwzględnienie poziomu cholesterolu przed badaniem zmniejszyło uzyskiwane błędy dla średnich i zawęziło przedziały ufności. By wyświetlić obserwowane lub oczekiwane średnie, wybieram odpowiednie ustawienia poprzez Opcje czynników, do tego zaznaczam wykres błędów. Pierwszy wykres przedstawia obserwowane średnie wraz z przedziałem ufności, tzn. nie uwzględniajace wypływu wieku i poziomu cholesterolu przed leczeniem; drugi wykres to oczekiwane na podstawie zbudowanego modelu średnie wraz z przedziałami ufności, tzn. po uwzględnieniu oddziaływania tych dwóch wspólzmiennych:

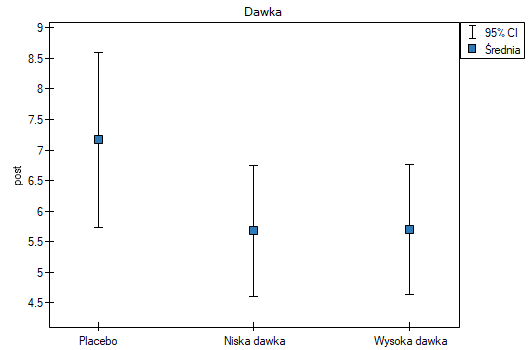
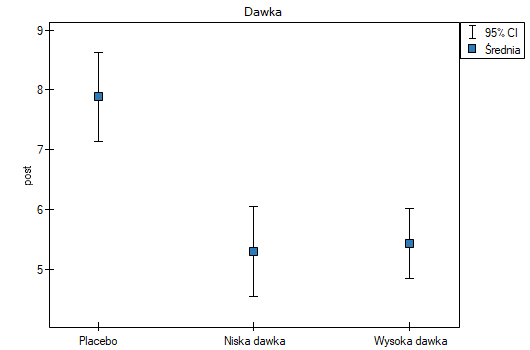
W efekcie uwzględniając poziom cholestrolu przed leczeniem badacz był w stanie wykazać skuteczność nowego sposobu leczenia. Poziom cholesterolu przed leczeniem i wiek tłumaczy w pewnym stopniu zmiany w poziemie cholesterolu po leczeniu, jednak pozostałą część zmian w 57% możemy przypisać zastosowanej dawce leku (cząstkowa Eta-kwadrat =0.565437). Testy post-hoc (wybrany poprzez Opcje czynników) zasugerowały powstanie dwóch grup jednorodnych, grupy placebo i grupy pacjentów z lekiem, wskazując że podnoszenie dawki do wysokiej nie ma znaczenia, gdyż uzyskane poziomy cholesterolu będą podobne.

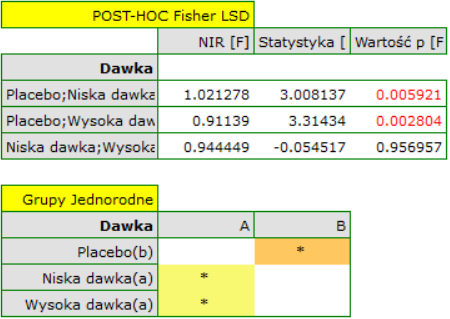
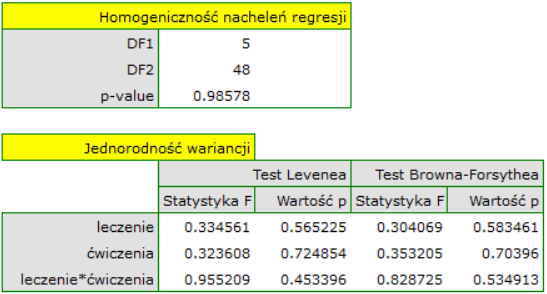
Pozostały do sprawdzenia założenia ANCOVA. Jednorodność wariancji i stałość nachleń prostych regresji potwierdzono przy pomocy testów

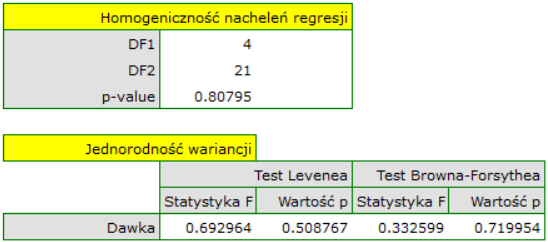
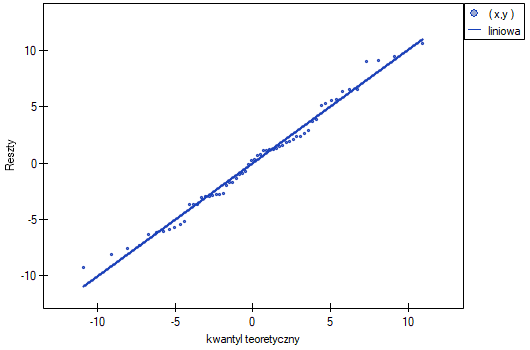
Normalność rozkładu reszy oceniono wizualnie wyrysowując wykresy Q-Q:

Przykład (plik stres.pqs)

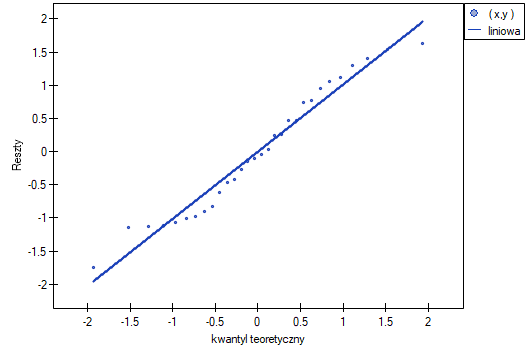
Przykład pochodzi z pakietu Datarium R-Cran.

Badacze chcą ocenić wpływ nowego leczenia i ćwiczeń na redukcję stresu po uwzględnieniu różnic w wieku. Wartość pomiaru stersu to interwałowa zmienna wynikowa Y. Ze względu na to, że zmienne „leczenie” i „ćwiczenia” mają odpowiednio 2 i 3 kategorie, przeprowadzimy dwukierunkową ANCOVA w celu określenia, czy interakcja między ćwiczeniami i leczeniem, przy jednoczesnym uwzględnieniu wieku badanych, ma związek ze stresem.

\begin{tabular}{|c|c|} \hline \multicolumn{2}{|c|}{Czynniki}\\ leczenie $X_1$ & ćwiczenia $X_2$ \\\hline \multirow{3}{*}{tak}& niewiele \\\cline{2-2} & przeciętnie \\\cline{2-2} & dużo\\\hline \multirow{3}{*}{nie}& niewiele \\\cline{2-2} & przeciętnie \\\cline{2-2} & dużo\\\cline{2-2} \hline \end{tabular}

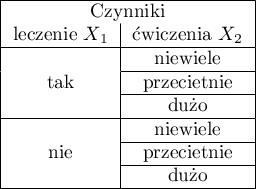
W oknie analizy jako zmienną zależną ustawiam „stres”, jako czynniki „leczenie” i „ćwiczenia” oraz dodaję interakcję tych dwóch zmiennych, współzmienna ciągła to „wiek”.

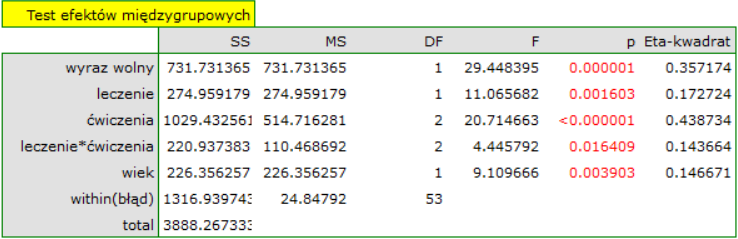
Uzyskany wynik pokazuje, że wpływ leczenia na stres zmienia się w zależności od intensywności wykonywania ćwiczeń - wskazuje na to istotna interakcja obu tych zmiennych (p=0.016409). Wyrysujemy wykres przedstawiający oczekiwane średnie poziomy stresu dla każdej z sześciu podgrup, na jakie interakcja podzieliła nasze dane oraz wyznaczymy testy post-hoc.

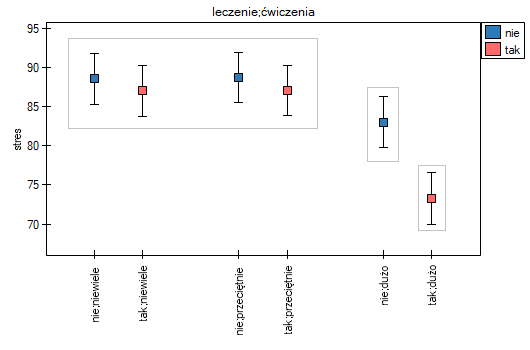
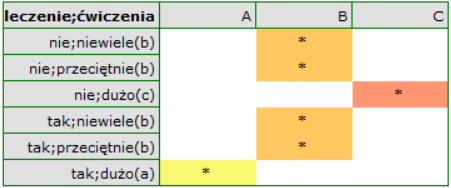
Zogodnie z wynikami testu post-hoc, możemy mówić o trzech różnych grupach jednorodnych: (B) grupa osób o wysokim poziomie stresu, to grupa ćwicząca niewiele lub przeciętnie (bez względu na to czy są to sosoby leczone czy nie), (C) grupa osób o niższym poziomie stresu, to grupa ćwicząca dużo i nieleczona, (A) grupa osób o najniższym poziomie stresu, to grupa ćwicząca dużo i leczona. Wartości poszczególnych średnich wraz z przedziałami ufności przedstawia tabela

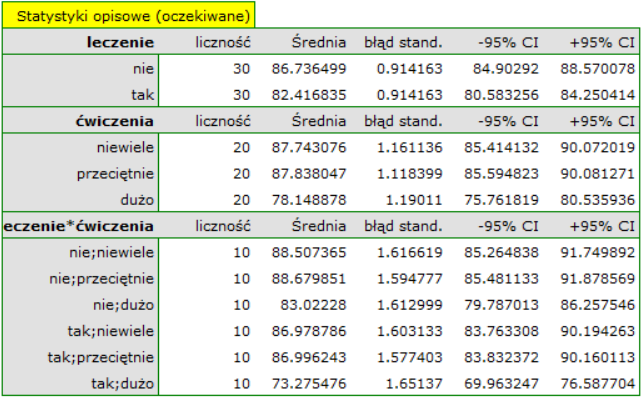
Założenia dotyczące równości wariancji, nachyleń linii regresji oraz normalności reszt modelu są spełnione