Test chi-kwadrat wariancji pojedynczej próby
Test  wariancji pojedynczej próby (ang. The Single-Sample Chi-square Test for a Population Variance) służy do weryfikacji hipotezy, że badana próba pochodzi z populacji dla której wariancja (lub odchylenie standardowe
wariancji pojedynczej próby (ang. The Single-Sample Chi-square Test for a Population Variance) służy do weryfikacji hipotezy, że badana próba pochodzi z populacji dla której wariancja (lub odchylenie standardowe 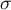 ) to zadana wartość. Przy czym hipotezy mogą dotyczyć zarówno wariancji jak i równoważnie odchylenia standardowego.
) to zadana wartość. Przy czym hipotezy mogą dotyczyć zarówno wariancji jak i równoważnie odchylenia standardowego.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu badanej cechy.
Hipotezy:
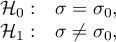
gdzie:
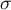 - odchylenie cechy w populacji reprezentowanej przez próbę,
- odchylenie cechy w populacji reprezentowanej przez próbę,
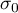 - zadana wartość.
- zadana wartość.
Statystyka testowa ma postać:
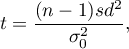
gdzie:
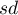 - odchylenie standardowe z próby,
- odchylenie standardowe z próby,
 - liczność próby.
- liczność próby.
Statystyka ta ma rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru: 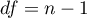 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Przy czym, jeśli wartość odchylenia standardowego jest mniejsza niż wartość zadana, to wartość  wyliczana jest jako podwojoną wartość pola pod krzywą rozkładu chi-kwadrat na lewo od odpowiedniej wartości krytycznej, a jeśli jest większa niż wartość zadana, jest to podwojoną wartość odpowiedniego pola po prawej stronie.
wyliczana jest jako podwojoną wartość pola pod krzywą rozkładu chi-kwadrat na lewo od odpowiedniej wartości krytycznej, a jeśli jest większa niż wartość zadana, jest to podwojoną wartość odpowiedniego pola po prawej stronie.
Okno z ustawieniami opcji testu chi-kwadrat wariancji pojedynczej próby wywołujemy poprzez menu Statystyka→Testy parametryczne→Chi-kwadrat dla wariancji.
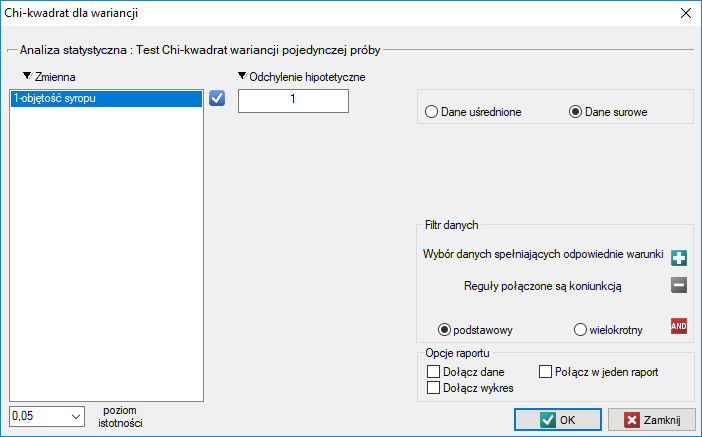
Uwaga!
Obliczenia mogą bazować na danych w postaci surowych rekordów lub danych uśrednionych tzn. odchyleniu standardowym i liczności próby.
Przed przystąpieniem do produkcji kolejnej partii pewnego syropu przeciwkaszlowego dokonano kontrolnych pomiarów objętości syropu nalewanego do butelek. Z dokumentacji technicznej urządzenia dozującego wynika, że dopuszczalny rozrzut objętości syropu mierzony za pomocą odchylenia standardowego wynosi 1ml. Należy sprawdzić, czy testowane urządzenie działa prawidłowo.}
Sprawdzono (testem Lillieforsa) normalność rozkładu objętości syropu nalewanego do butelek uzyskując wynik zgodny z tym rozkładem. Analiza dotycząca odchylenia standardowego może być więc przeprowadzona testem chi-kwadrat dla wariancji.
Hipotezy:


Porównując wartość 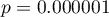 testu
testu  z poziomem istotności
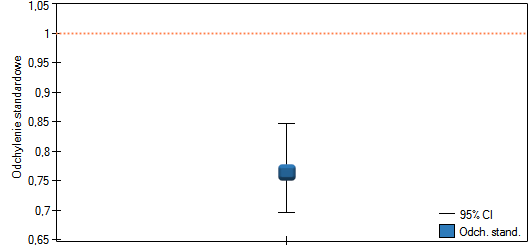
z poziomem istotności  stwierdzamy, że rozrzut urządzenia dozującego jest inny niż 1ml. Działanie urządzenia możemy jednak uznać za prawidłowe, ponieważ odchylenie standardowe w próbie wynosi 0.76 i jest istotnie mniejsze niż dopuszczalna wartość wynikająca z dokumentacji technicznej.
stwierdzamy, że rozrzut urządzenia dozującego jest inny niż 1ml. Działanie urządzenia możemy jednak uznać za prawidłowe, ponieważ odchylenie standardowe w próbie wynosi 0.76 i jest istotnie mniejsze niż dopuszczalna wartość wynikająca z dokumentacji technicznej.