Testy dla jednej proporcji
Testy dla jednej proporcji stosujemy, gdy mamy do uzyskania dwa możliwe wyniki (jeden z nich to wynik wyróżniony o liczności 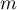 ) i wiemy, jak często te wyniki pojawiają się w próbie (znamy proporcję
) i wiemy, jak często te wyniki pojawiają się w próbie (znamy proporcję  ). W zależności od wielkości próby
). W zależności od wielkości próby  mamy do wyboru test
mamy do wyboru test  dla jednej proporcji
dla jednej proporcji  dla dużych prób oraz test dokładny dwumianowy
dla dużych prób oraz test dokładny dwumianowy  dla prób o małej liczności. Testy te służą do weryfikacji hipotezy, że proporcja w populacji z której pochodzi próba to zadana wartość.
dla prób o małej liczności. Testy te służą do weryfikacji hipotezy, że proporcja w populacji z której pochodzi próba to zadana wartość.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę.
Dodatkowy warunek dla testu  dla jednej proporcji:
dla jednej proporcji:
Hipotezy:
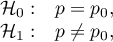
gdzie:

 prawdopodobieństwo (wyróżniona proporcja) w populacji,
prawdopodobieństwo (wyróżniona proporcja) w populacji,
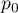
 prawdopodobieństwo oczekiwane (proporcja oczekiwana).
prawdopodobieństwo oczekiwane (proporcja oczekiwana).
Test  dla jednej proporcji
dla jednej proporcji
Test  dla jednej proporcji (ang. Z test for one proportion).
dla jednej proporcji (ang. Z test for one proportion).
Statystyka testowa ma postać:
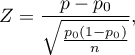 gdzie:
gdzie:
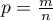 proporcja dla próby z tej populacji,
proporcja dla próby z tej populacji,
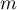 -liczność wartości wyszczególnionych w próbie,
-liczność wartości wyszczególnionych w próbie,
 - liczność próby.
- liczność próby.
Zmodyfikowana o poprawkę na ciągłość statystyka testowa ma postać:
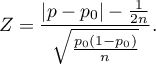
Statystyka  bez korekcji na ciągłość jak i z tą korekcją ma asymptotycznie (dla dużych liczności) rozkład normalny.
bez korekcji na ciągłość jak i z tą korekcją ma asymptotycznie (dla dużych liczności) rozkład normalny.
Test dwumianowy
Test dwumianowy (ang. Binominal test for one proportion) wykorzystuje w sposób bezpośredni rozkład dwumianowy zwany również rozkładem Bernoulliego, który należy do grupy rozkładów dyskretnych (czyli takich, w których badana zmienna przyjmuje skończoną liczbę wartości). Analizowana zmienna może przyjmować 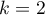 wartości, pierwszą oznaczaną zwykle mianem sukcesu a drugą porażki. Prawdopodobieństwo wystąpienia sukcesu to
wartości, pierwszą oznaczaną zwykle mianem sukcesu a drugą porażki. Prawdopodobieństwo wystąpienia sukcesu to 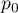 , a porażki
, a porażki 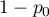 .
.
Prawdopodobieństwo dla konkretnego punktu w tym rozkładzie wyliczane jest ze wzoru:
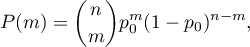 gdzie:
gdzie:
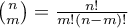 ,
,
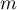 - liczność wartości wyszczególnionych w próbie,
- liczność wartości wyszczególnionych w próbie,
 - liczność próby.
- liczność próby.
Na podstawie sumy odpowiednich prawdopodobieństw 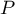 wyznacza się wartość
wyznacza się wartość  jednostronną i dwustronną, przy czym dwustronna wartość
jednostronną i dwustronną, przy czym dwustronna wartość  jest definiowana jako podwojona wartość mniejszego z jednostronnych prawdopodobieństw. Wartość
jest definiowana jako podwojona wartość mniejszego z jednostronnych prawdopodobieństw. Wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
Dla estymatora z próby jakim jest w tym przypadku wartość proporcji  wyznacza się przedział ufności. Dla prób o dużej liczności można bazować na przedziałach opartych o rozkład normalny - tzw. przedziały Walda. Bardziej uniwersalne są natomiast przedziały zaproponowane przez Wilsona (1927)2) a także Agresti i Coull (1998)3). Przedziały Cloppera i Pearsona (1934)4) są dokładniejsze dla prób o mniejszej liczności.
wyznacza się przedział ufności. Dla prób o dużej liczności można bazować na przedziałach opartych o rozkład normalny - tzw. przedziały Walda. Bardziej uniwersalne są natomiast przedziały zaproponowane przez Wilsona (1927)2) a także Agresti i Coull (1998)3). Przedziały Cloppera i Pearsona (1934)4) są dokładniejsze dla prób o mniejszej liczności.
Porównanie metod budowania przedziałów dla proporcji można znaleźć w pracy Brown L.D i innych (2001)5).
Okno z ustawieniami opcji testu Z dla jednej proporcji wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Z dla proporcji.
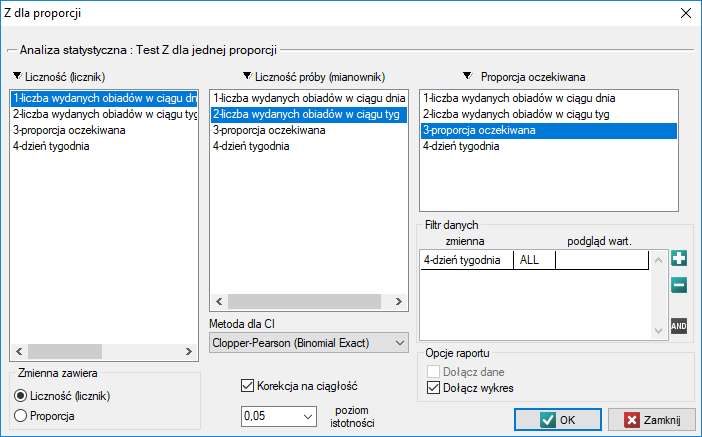
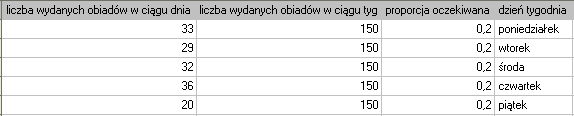
Przykład c.d. (plik obiady.pqs)
Załóżmy, że chcielibyśmy sprawdzić, czy w piątek wydawana jest 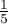 spośród wszystkich obiadów wydawanych w szkolnej stołówce w ciągu tygodnia. Dla pobranej próby
spośród wszystkich obiadów wydawanych w szkolnej stołówce w ciągu tygodnia. Dla pobranej próby  ,
, 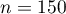 .
.
Przy ustawianiu opcji analizy włączamy filtr wybierając odpowiedni dzień tygodnia - czyli piątek. Brak ustawienia filtru nie generuje błędu a jedynie wyliczenie kolejnych statystyk dla kolejnych dni tygodnia.
Hipotezy:
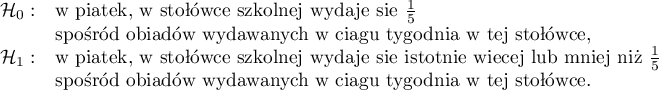
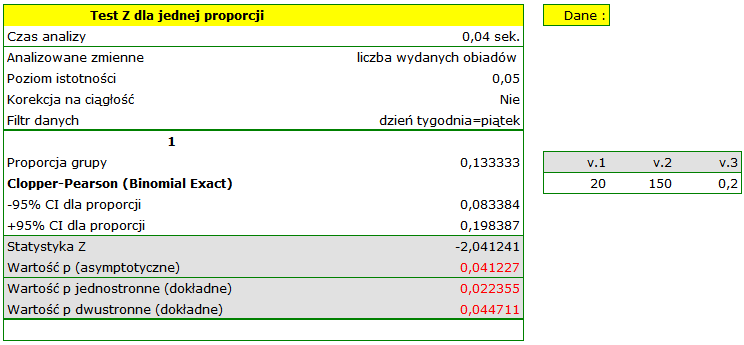
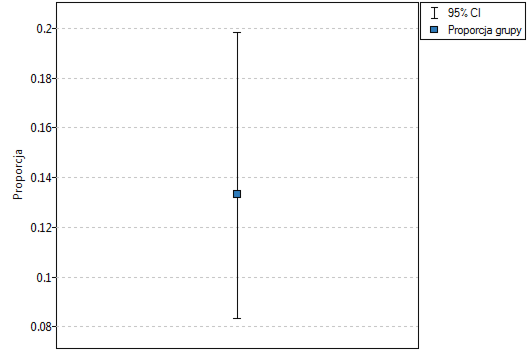
Proporcja wartości wyróżnionych w próbie to 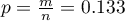 a 95% przedział ufności Cloppera-Pearsona dla tej frakcji
a 95% przedział ufności Cloppera-Pearsona dla tej frakcji 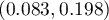 nie zawiera hipotetycznej wartości 0.2.
nie zawiera hipotetycznej wartości 0.2.
Na podstawie testu  bez poprawki na ciągłość (
bez poprawki na ciągłość ( =0.041227) jak i na podstawie dokładnej wartości prawdopodobieństwa wyliczonego z rozkładu dwumianowego (
=0.041227) jak i na podstawie dokładnej wartości prawdopodobieństwa wyliczonego z rozkładu dwumianowego ( =0.044711) moglibyśmy przyjąć (na poziomie istotności
=0.044711) moglibyśmy przyjąć (na poziomie istotności  ), że w piątek wydaje się statystycznie mniej niż
), że w piątek wydaje się statystycznie mniej niż 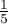 obiadów wydawanych przez cały tydzień. Po zastosowaniu poprawki na ciągłość jednak nie udaje się odrzucić hipotezy zerowej (
obiadów wydawanych przez cały tydzień. Po zastosowaniu poprawki na ciągłość jednak nie udaje się odrzucić hipotezy zerowej ( =0.052479).
=0.052479).

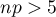 i
i 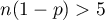 ).
).