The t-test for dependent groups
The  -test for dependent groups is used when the measurement of an analysed variable you do twice, each time in different conditions (but you should assume, that variances of the variable in both measurements are pretty close to each other). We want to check how big is the difference between the pairs of measurements (
-test for dependent groups is used when the measurement of an analysed variable you do twice, each time in different conditions (but you should assume, that variances of the variable in both measurements are pretty close to each other). We want to check how big is the difference between the pairs of measurements (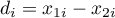 ). This difference is used to verify the hypothesis informing us that the mean of the difference in the analysed population is 0.
). This difference is used to verify the hypothesis informing us that the mean of the difference in the analysed population is 0.
Basic assumptions:
- measurement on an interval scale,
- normality of distribution of measurements
 (or the normal distribution for an analysed variable in each measurement),
(or the normal distribution for an analysed variable in each measurement),
Hypotheses:
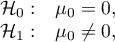
where:
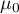 , – mean of the differences
, – mean of the differences 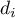 in a population.
in a population.
The test statistic is defined by:
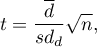
where:
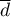 – mean of differences
– mean of differences 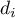 in a sample,
in a sample,
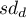 – standard deviation of differences
– standard deviation of differences 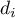 in a sample,
in a sample,
 – number of differences
– number of differences 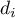 in a sample.
in a sample.
Test statistic has the t-Student distribution with  degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Note
- standard deviation of the difference is defined by:
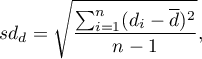
- standard error of the mean of differences is defined by:
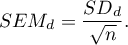
Standardized effect size.
The Cohen's d determines how much of the variation occurring is the difference between the averages, while taking into account the correlation of the variables.
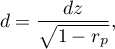 .
.
When interpreting an effect, researchers often use general guidelines proposed by Cohen 1) defining small (0.2), medium (0.5) and large (0.8) effect sizes.
The settings window with the t-test for dependent groups can be opened in Statistics menu→Parametric tests→t-test for dependent groups or in ''Wizard''.
Note
Calculations can be based on raw data or data that are averaged like: arithmetic mean of difference, standard deviation of difference and sample size.
A clinic treating eating disorders studied the effect of a recommended „diet A” on weight change. A sample of 120 obese patients were put on the diet. Their BMI levels were measured twice: before the diet and after 180 days of the diet. To test the effectiveness of the diet, the obtained BMI measurements were compared.
Hypotheses:
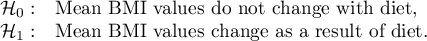
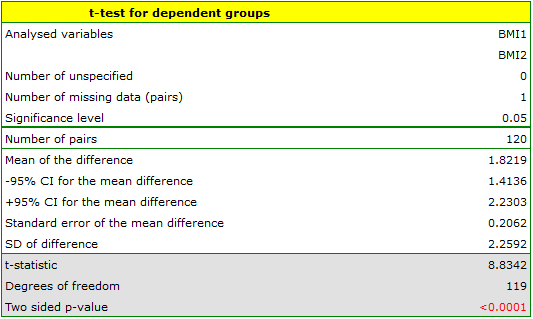
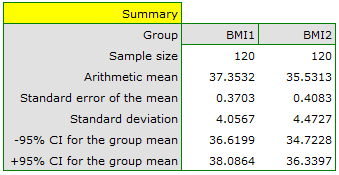
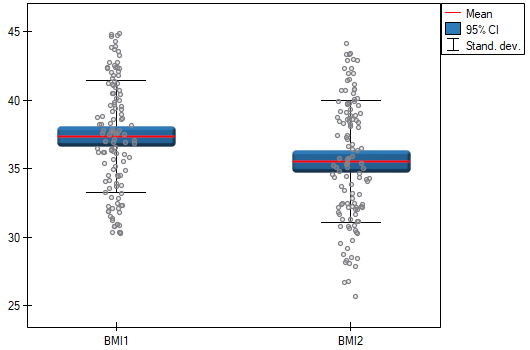
Comparing 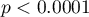 with a significance level
with a significance level  we find that the mean BMI level changed significantly. Before the diet, it was higher by less than 2 units on average.
we find that the mean BMI level changed significantly. Before the diet, it was higher by less than 2 units on average.
The study was able to use the Student's t-test for dependent groups because the distribution of the difference between pairs of measurements was a normal distribution (Lilliefors test, 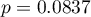 ).
).
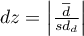 ,
,
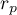 –
–