pl:statpqpl:usepl:arkpl:macppl

Macierz podobieństwa

Wzajemne relacje między obiektami mogą być wyrażone przez ich odległości lub bardziej ogólnie poprzez niepodobieństwo. Czym dalej od siebie znajdują się obiekty, tym bardziej są do siebie niepodobne, im bliżej natomiast, tym podobieństwo między nimi jest większe. Badać można odległość obiektów pod względem wielu cech np. gdy porównywane obiekty to miasta ich podobieństwo możemy definiować między innymi w oparciu o: długość drogi je łączącej, gęstości zaludnienia, PKB przypadającym na mieszkańca, emisję zanieczyszczeń, przeciętne ceny nieruchomości itd. Mając tak wiele różnych cech badacz tak musi dobrać miarę odległości, by najlepiej obrazowała rzeczywiste podobieństwo obiektów.

Okno z ustawieniami opcji macierzy podobieństwa wywołujemy poprzez menu Dane→Macierz podobieństwa…

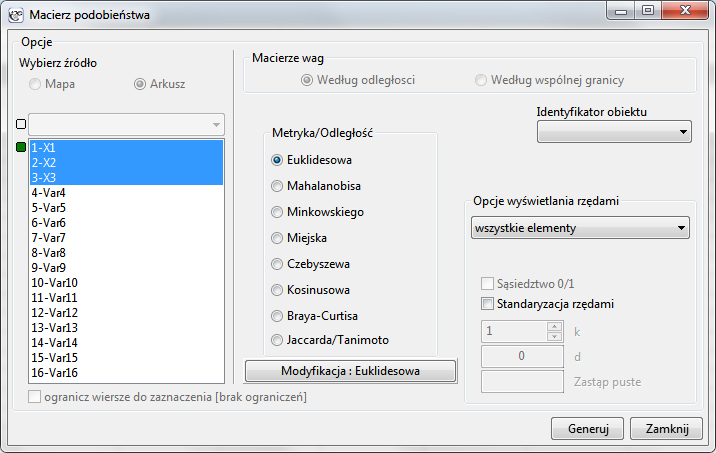
Niepodobieństwo/podobieństwo obiektów wyrażamy za pomocą odległości będących najczęściej metryką. Nie każda miara odległości jest jednak metryką. Aby odległość mogła być nazwana metryką musi spełniać 4 warunki:

odległość pomiędzy obiektami nie może być ujemna: $d(x_1, x_2) \geq 0$ ,
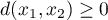odległość między dwoma obiektami wynosi 0 wtedy i tylko wtedy gdy są one identyczne: $d(x_1, x_2) = 0 \Longleftrightarrow x_1 = x_2$ ,
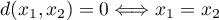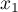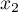odległość musi być symetryczna, tzn. odległość z obiektu $x_1$ do $x_2$ musi być taka sama jak z 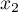$x_2$ do $x_1$ : $d(x, y) = d(y, x)$ ,
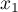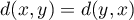odległość musi spełniać warunek trójkąta: $d(x, z) \leq (x, y) + d(y, z)$ .

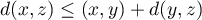Uwaga!
Metryki powinny być wyliczane dla cech o tych samych zakresach wartości. Gdyby tak nie było to cechy o wyższych zakresach miałyby większy wpływ na uzyskany wynik podobieństwa niż te o niższych zakresach. Przykładowo, wyliczając podobieństwo osób możemy oprzeć je na takich cechach jak min. masa ciała i wiek. Wówczas masa ciała w kilogramach, w zakresie od 40 do 150 kg, będzie miała większy wpływ na wynik niż wiek w latach, w zakresie od 18 do 90 lat. By wpływ każdej cechy na uzyskany wynik podobieństwa był zrównoważony powinniśmy każdą z nich znormalizować/wystandaryzować przed przystąpieniem do analizy. Chcąc natomiast samodzielnie zdecydować o wielkości tego wpływu, po zastosowaniu standaryzacji, wskazując rodzaj metryki należy wpisać nadane przez siebie wagi.

Odległość/Metryka:

Euklidesowa
Kiedy mówimy o odległości nie definiując jej rodzaju zakładamy, że jest to odległość Euklidesowa - najpopularniejszy typ odległości stanowiący naturalny element modeli świata rzeczywistego. Odległość euklidesowa jest metryką i dana jest wzorem:
$\begin{displaymath} d(x_1,x_2)=\sqrt{\sum_{k=1}^n\left(x_{1k}-x_{2k}\right)^2} \end{displaymath}$

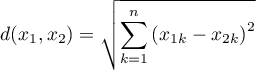
Minkowskiego
Odległość Minkowskiego definiowana jest dla parametrów $p$ i $r$ równych sobie - jest wówczas metryką. Ten rodzaj metryki pozwala sterować procesem wyliczania podobieństwa poprzez podanie wartości $p$ i $r$ ujętymi we wzorze:
$\begin{displaymath} d(x_1,x_2)=\sqrt[p]{\sum_{k=1}^n\left|x_{1k}-x_{2k}\right|^r} \end{displaymath}$
Zwiększając parametr $r$ zwiększamy wagę przypisaną różnicy pomiędzy obiektami dla każdej cechy, zmieniając $p$ nadajemy większe/mniejsze znaczenie obiektom bliższym/dalszym. Jeśli $r$ i $p$ są równe 2, to odległość Minkowskiego sprowadza się do odległości Euklidesowej, jeśli są równe 1, do odległości Miejskiej, a przy tych parametrach dążących do nieskończoności, do metryki Czebyszewa.

Miejska (inaczej: odległość Manhattan lub odległość taksówkowa)
To odległość pozwalająca na poruszanie się tylko w dwóch prostopadłych do siebie kierunkach. Ten rodzaj odległości przypomina poruszanie się po prostopadle przecinających się ulicach (kwadratowa sieć ulic przypominająca plan Manhattanu). Metryka ta dana jest wzorem:
$\begin{displaymath} d(x_1,x_2)=\sum_{k=1}^n|x_{1k}-x_{2k}| \end{displaymath}$

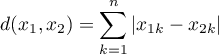
Czebyszewa
Odległość pomiędzy porównywanymi obiektami to największa z uzyskanych odległości dla poszczególnych cech tych obiektów:
$\begin{displaymath} d(x_1,x_2)=\max_{k}|x_{1k}-x_{2k}| \end{displaymath}$

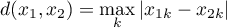
Mahalanobisa
Odległość Mahalanobisa nazywana jest również odległością statystyczną. Jest to odległość ważona macierzą kowariancji, przez co porównywać można obiekty opisane wzajemnie skorelowanymi cechami. Stosowanie odległości Mahalanobisa daje dwie podstawowe korzyści:
1) Zmienne, dla których obserwowane są większe odchylenia lub większe zakresy wartości nie mają zwiększonego wpływu na wynik odległości Mahalanobisa (stosując macierz kowariancji standaryzujemy bowiem zmienne wykorzystując wariancję znajdującą się na diagonali). W rezultacie przed przystąpieniem do analizy nie ma wymogu standaryzowania/normalizacji zmiennych.
2) Bierze pod uwagę wzajemne skorelowanie cech opisujących porównywane obiekty (stosując macierz kowariancji wykorzystujemy informację o zależności między cechami znajdującą się poza przekątną macierzy).
$\begin{displaymath} d(x_1,x_2)=\sqrt{(\vec{x}-\vec{y})^TS^{-1}(\vec{x}-\vec{y})} \end{displaymath}$
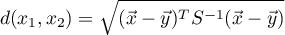
Wyliczona w ten sposób miara spełnia warunki metryki.

Kosinusowa
Odległość kosinusowa powinna być wyliczana na danych dodatnich ponieważ nie jest ona metryką (nie spełnia pierwszego warunku: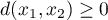 $d(x_1, x_2) \geq 0$ ). Jeśli więc mamy cechy przyjmujące również wartości ujemne powinnyśmy je wcześniej przekształcić stosując np. normalizację do przedziału rozpiętego na liczbach dodatnich. Zaletą tej odległości jest fakt, że (dla dodatnich argumentów) ograniczona jest do przedziału [0, 1]. Podobieństwo dwóch obiektów reprezentuje kąt pomiędzy dwoma wektorami przedstawiającymi cechy tych obiektów.
$\begin{displaymath} d(x_1,x_2)=1-K, \end{displaymath}$
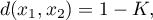
Gdzie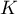 $K$ to współczynnik podobieństwa (kosinus kąta pomiędzy dwoma znormalizowanymi wektorami):
$\begin{displaymath} K=\frac{\sum_{k=1}^nx_{1k}x_{2k}}{\sqrt{\sum_{k=1}^nx_{1k}^2}\sqrt{\sum_{k=1}^nx_{2k}^2}} \end{displaymath}$
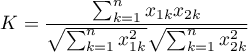
Obiekty są podobne, gdy wektory się pokrywają - wtedy kosinus kąta (podobieństwo) wynosi 1 odległość (niepodobieństwo) 0. Obiekty są różne, gdy wektory są prostopadłe - wtedy kosinus kąta (podobieństwo) wynosi 0 odległość (niepodobieństwo) wynosi 1.

Przykład - porównanie tekstów
Tekst 1: na tym przystanku wsiadło kilka osób a na następnym wysiadła jedna
Tekst 2: na przystanku jedna Pani wysiadła a kilka wsiadło
Chcemy wiedzieć, jak podobne są teksty pod względem liczby tych samych słów, nie interesuje nas natomiast kolejność występowania słów.
Tworzymy listę słów z obu tekstów i liczymy jak często wystąpiło każde słowo:

$\begin{tabular}{|c||c|c|c|c|c|c|c|c|c|c|c|c|} \hline \textbf{SŁOWA}&na&tym&przystanku&wsiadło&kilka&osób&a&następnym&wysiadła&jedna&Pani\\ \hline \textbf{tekst 1}&2&1&1&1&1&1&1&1&1&1&0\\ \textbf{tekst 2}&1&0&1&1&1&0&1&0&1&1&1\\\hline \end{tabular}$

Kosinus kąta pomiędzy wektorami wynosi 0,784465, a więc odległość miedzy nimi nie jest duża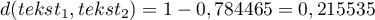 $d(tekst_1,tekst_2)=1-0,784465=0,215535$ .
Na podobnej zasadzie możemy porównywać dokumenty pod względem występowania słów kluczowych, tak by znajdować te najbardziej odpowiadające zapytaniu.

Braya-Curtisa
Odległość (miara niepodobieństwa) Bray'a-Curtis'a powinna być wyliczana na danych dodatnich ponieważ nie jest ona metryką (nie spełnia pierwszego warunku: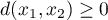 $d(x_1, x_2) \geq 0$ ). Jeśli mamy cechy przyjmujące również wartości ujemne, powinnyśmy je wcześniej przekształcić stosując np. normalizację do przedziału rozpiętego na liczbach dodatnich. Zaletą tej odległości jest fakt, że (dla dodatnich argumentów) ograniczona jest do przedziału [0, 1], gdzie 0 - oznacza, że porównywane obiekty są podobne, 1 - niepodobne.
$\begin{displaymath} d(x_1,x_2)=\frac{\sum_{k=1}^n|x_{1k}-x_{2k}|}{\sum_{k=1}^n(x_{1k}+x_{2k})} \end{displaymath}$
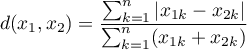
Wyliczając miarę podobieństwa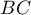 $BC$ od wartości 1 odejmujemy odległość Bray'a-Curtis'a:
$\begin{displaymath} BC=1-d(x_1,x_2) \end{displaymath}$

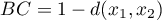
Jaccarda
Odległość (miara niepodobieństwa) Jaccarda wyliczana jest dla zmiennych binarnych (Jaccard, 1901), gdzie 1 oznacza występowanie danej cech 0- jej brak.

$\begin{tabular}{|c|c||c|c|} \hline \multicolumn{2}{|c||}{ }& \multicolumn{2}{|c|}{objekt 1} \cline{3-4} \multicolumn{2}{|c||}{ }& 1 & 0 \\ \hline \hline \multirow{}{}{objekt 2}& 1 & a & b \\ \cline{2-4} & 0 & c & d\\ \hline \end{tabular}$

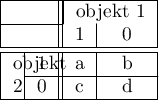
Odległość Jacckarda wyraża się wzorem:
$\begin{displaymath} d(x_1,x_2)=1-J. \end{displaymath}$
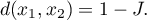
gdzie:

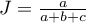$J=\frac{a}{a+b+c}$ - współczynnik podobieństwa Jaccarda.

Współczynnik podobieństwa Jaccarda zawiera się w przedziale [0,1], gdzie 1 oznacza najwyższe podobieństwo, 0 - najniższe. Odległość (niepodobieństwo) interpretujemy przeciwnie: 1 - oznacza, że porównywane obiekty są niepodobne, 0 - że bardzo podobne.
Sens współczynnika podobieństwa Jaccarda dobrze opisuje sytuacja dotycząca wyboru towaru przez klientów. Przez 1 oznaczymy fakt zakupu danego produktu przez klienta, 0 - klient nie kupił tego artykułu. Wyliczając współczynnik Jaccarda porównamy 2 produkty by dowiedzieć się jaka część klientów kupuje je w tandemie. Nie interesuje nas oczywiście informacja o klientach, którzy nie kupili żadnego z porównywanych artykułów. Jesteśmy natomiast ciekawi jak wiele osób wybierających jeden z porównywanych produktów wybiera jednocześnie ten drugi. Suma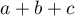 $a+b+c$ - to liczba klientów, którzy wybrali któryś z porównywanych artykułów, 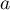$a$ - to liczba klientów wybierających oba artykuły jednocześnie. Im wyższy współczynnik podobieństwa Jaccarda, tym bardziej nierozerwalne są artykuły (zakupowi jednego towarzyszy zakup drugiego). Odwrotnie będzie, gdy dostaniemy wysoki współczynnik niepodobieństwa Jaccarda. Będzie on świadczył o dużej konkurencyjności artykułów, tzn. zakup jednego będzie powodował brak zakupu drugiego.
Wzór na współczynnik podobieństwa Jaccarda można również zapisać w ogólnej postaci:

$J=\frac{\sum_{k=1}^nx_{1k}x_{2k}}{\sum_{k=1}^nx_{1k}^2\sum_{k=1}^nx_{2k}^2-\sum_{k=1}^nx_{1k}x_{2k}}$

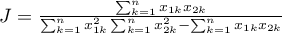
zaproponowanej przez Tanimoto (1957). Ważną cechą formuły Tanimoto jest fakt, że może być wyliczana także dla cech ciągłych.
W przypadku danych binarnych wzory na niepodobieństwo/podobieństwo Jaccarda i Tanimoto są tożsame i spełniają warunki metryki. Natomiast dla zmiennych ciągłych wzór Tanimoto nie jest metryką (nie spełnia warunku trójkąta).

Przykład - porównanie gatunków
Badamy podobieństwo pod względem genetycznym przedstawicieli trzech różnych gatunków - w sensie ilości genów które są dla nich wspólne. Jeśli gen występuje w organizmie, to dajemy mu wartość 1, 0 - w przeciwny przypadku. Dla prostoty przykładu analizie poddanych jest zaledwie 10 genów.

$\begin{tabular}{|c||c|c|c|c|c|c|c|c|c|c|} \hline \textbf{GENY}&gen1&gen2&gen3&gen4&gen5&gen6&gen7&gen8&gen9&gen10\\ \hline \textbf{osobnik1}&0&1&1&1&1&1&1&0&1&0\\ \textbf{osobnik2}&0&0&1&1&1&1&1&0&1&0\\ \textbf{osobnik3}&1&0&1&1&0&0&1&0&0&0\\ \hline \end{tabular}$

Wyliczona macierz podobieństwa przedstawia się następująco:

$\begin{tabular}{|c||c|c|c|} \hline \textbf{OBIEKTY}&osobnik1&osobnik2&osobnik3\\ \hline \textbf{osobnik1}&0&0.857143&0.375\\ \textbf{osobnik2}&0.857143&0&0.428571\\ \textbf{osobnik3}&0.375&0.428571&0\\ \hline \end{tabular}$

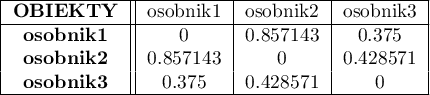
Najbardziej podobni są osobnicy 1 i 2 a najmniej 1 i 3:
- podobieństwo Jaccarda osobnika1 i osobnika2 wynosi 0.857143, czyli nieco ponad 85% genów występujących w obu porównywanych gatunkach jest dla nich wspólna.
- podobieństwo Jaccarda osobnika1 i osobnika3 wynosi 0.375, czyli ponad 37% genów występujących w obu porównywanych gatunkach jest dla nich wspólna.
- podobieństwo Jaccarda osobnika2 i osobnika3 wynosi 0.428571, czyli prawie 43% genów występujących w obu porównywanych gatunkach jest dla nich wspólna.

Opcje macierzy podobieństwa
wykorzystujemy do wskazania sposobu zwracania elementów w macierzy. Standardowo zwracane są wszystkie elementy macierzy, w takiej formie w jakiej były wyliczone zgodnie z przyjętą metryką. Możemy to zmienić ustawiając:

Elementy macierzy:
- minimum - oznacza, że w każdym wierszu macierzy zostanie wyświetlona tylko wartość minimalna i wartość na głównej przekątnej;
- maksimum - oznacza, że w każdym wierszu macierzy zostanie wyświetlona tylko wartość maksymalna i wartość na głównej przekątnej;
- $k$ minimalnych - oznacza, że w każdym wierszu macierzy zostanie wyświetlonych tyle najmniejszych wartości ile wskaże użytkownik podając wartość $k$ oraz wartość na głównej przekątnej;
- $k$ maksymalnych - oznacza, że w każdym wierszu macierzy zostanie wyświetlonych tyle największych wartości ile wskaże użytkownik podając wartość $k$ oraz wartość na głównej przekątnej;
- elementy poniżej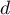 $d$ - oznacza, że w każdym wierszu macierzy zostaną wyświetlone te elementy, których wartość będzie mniejsza niż wskazana przez użytkownika wielkość 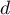$d$ oraz wartość na głównej przekątnej;
- elementy powyżej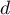 $d$ - oznacza, że w każdym wierszu macierzy zostaną wyświetlone te elementy, których wartość będzie większa niż wskazana przez użytkownika wielkość $d$ oraz wartość na głównej przekątnej;
Sąsiedztwo 0/1
Wybierając opcję Sąsiedztwo 0/1 wartości wewnątrz macierzy zastępujemy wartością 1, a miejsca puste wartością 0. W ten sposób oznaczamy na przykład czy obiekty sąsiadują (1) czy nie (0), czyli wyznaczamy macierz sąsiedztwa.
Standaryzacja rzędami
Standaryzacja rzędami oznacza, że każdy element macierzy dzielony jest przez sumę wiersza macierzy. W rezultacie uzyskane wartości znajdują się w przedziale od 0 do 1.
Zastąp puste
Opcja Zastąp puste pozwala na wpisanie wartości jaka ma zostać umieszczona w macierzy w miejscu ewentualnych pustych elementów.
Wybrany identyfikator obiektu pozwala nazwać wiersze i kolumny macierzy podobieństwa zgodnie z nazewnictwem przechowywanym we wskazanej zmiennej.

Przykład (plik: podobienstwoLokali.pqs)

W procedurach wyceny nieruchomości, zarówno ze względów merytorycznych jak też prawnych, kwestia podobieństwa pełni ważną rolę. Jest na przykład zasadniczą przesłanką umożliwiającą grupowanie obiektów i przypisywanie do odpowiedniego segmentu.

Załóżmy, że do pośrednika nieruchomości zgłasza się osoba poszukująca mieszkania, która definiuje te cechy, które lokal musi posiadać i te, które mają duży wpływ na decyzję o zakupie ale nie są decydujące. Cechy, które lokal musi posiadać to:

nieruchomość lokalowa (stanowiąca przedmiot odrębnej własności),
położona w dzielnicy A,
położona w niskiej zabudowie wielorodzinnej (do 5-ciu kondygnacji),
nie remontowana (standard przeciętny lub pogorszony).

Dane dotyczące tych lokali zebrano w tabeli, gdzie 1 oznacza, że lokal spełnia warunki wyszukiwania, 0 że ich nie spełnia.

Te lokale, które nie spełniają warunków wyszukiwania wyłączymy z analizy poprzez dezaktywację odpowiednich wierszy. Poprzez menu Edycja→Aktywuj/Dezaktywuj (filtr)… dezaktywujemy te wiersze, które nie spełniają choćby jednego z postawionych warunków.

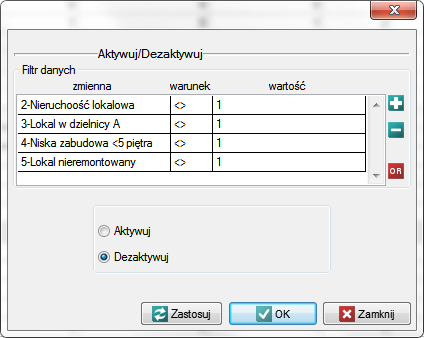
Pamiętamy by warunki dezaktywacji połączone były alternatywą (zmieniamy na ).

W rezultacie wyłoniono 11 lokali (lokal 10, 12, 17, 35, 88, 101, 105, 122, 130, 132, 135) pasujących do tego segmentu (spełniających wszystkie 4 warunki).

Teraz weźmiemy pod uwagę te cechy, które mają duży wpływ na decyzję klienta, ale nie są decydujące:

Liczba pokoi = 3;
Piętro na którym znajduje się lokal = 0;
Wiek budynku w którym znajduje się lokal = ok. 3 lata;
Bliskość centrum dzielnicy A (czas jaki zajmuje dotarcie do centrum) = ok. 30 min;
Bliskość przystanku komunikacji miejskiej = ok. 80 m.

$\begin{tabular}{|c||c|c|c|c|c|} \hline &\textbf{Liczba}&\textbf{Piętro}&\textbf{Wiek}&\textbf{Dystans}&\textbf{Odległość}\\ &\textbf{pokoi}&\textbf{lokalu}&\textbf{budynku}&\textbf{do centrum}&\textbf{przystanku}\\\hline\hline \rowcolor[rgb]{0.75,0.75,0.75}Poszukiwany&3&0&3&30&80\\ Lokal 10&2&1&1&0&150\\ Lokal 12&1&2&1&0&200\\ Lokal 17&3&1&7&20&500\\ Lokal 35&2&0&6&5&100\\ Lokal 88&3&4&6&5&200\\ Lokal 101&4&2&10&0&10\\ Lokal 105&2&2&6&0&50\\ Lokal 122&1&0&6&5&100\\ Lokal 130&2&0&10&0&20\\ Lokal 132&3&5&6&30&400\\ Lokal 135&3&1&6&5&100\\ \hline \end{tabular}$

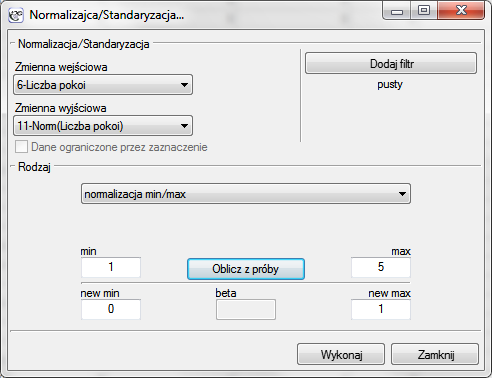
Zauważmy, że ostatnia cecha, czyli odległość przystanku komunikacji miejskiej jest wyrażona znacznie większymi liczbami niż pozostałe cechy porównywanych lokali. W rezultacie cecha ta będzie miała znacznie większy wpływ na uzyskany wynik macierzy odległości niż pozostałe cechy. Chcąc temu zapobiec przed analizą normalizujemy wszystkie cechy wybierając dla nich wspólny zakres od 0 do 1 - w tym celu korzystamy z menu Dane→Normalizacja/Standaryzacja…. W oknie normalizacji jako zmienną wejściową ustawiamy „Liczbę pokoi”, a jako zmienną wyjściową pustą zmienną nazwaną „Norm(Liczba pokoi)”; rodzaj normalizacji to normalizacja min/max; wartości min i max wyliczamy z próby wybierając przycisk Oblicz z próby - wynik normalizacji zostanie zwrócony do arkusza danych po wybraniu przycisku Wykonaj. Normalizację powtarzamy dla kolejnych zmiennych czyli: „Piętra”, „Wieku budynku”, „Dystansu do centrum” i „Odległości przystanku”.

Znormalizowane dane przedstawia poniższa tabela.

$\begin{tabular}{|c||c|c|c|c|c|} \hline &\footnotesize{\textbf{Norm(Liczba}}&\footnotesize{\textbf{Norm(Piętro}}&\footnotesize{\textbf{Norm(Wiek}}&\footnotesize{\textbf{Norm(Dystans}}&\footnotesize{\textbf{Norm(Odległość}}\\ &\footnotesize{\textbf{pokoi)}}&\footnotesize{\textbf{lokalu)}}&\footnotesize{\textbf{budynku)}}&\footnotesize{\textbf{do centrum)}}&\footnotesize{\textbf{przystanku)}}\\\hline \rowcolor[rgb]{0.75,0.75,0.75}Poszukiwany&0,666666667&0&0,222222222&1&0,142857143\\ Lokal 10&0,333333333&0,2&0&0&0,285714286\\ Lokal 12&0&0,4&0&0&0,387755102\\ Lokal 17&0,666666667&0,2&0,666666667&0,666666667&1\\ Lokal 35&0,333333333&0&0,555555556&0,166666667&0,183673469\\ Lokal 88&0,666666667&0,8&0,555555556&0,166666667&0,387755102\\ Lokal 101&1&0,4&1&0&0\\ Lokal 105&0,333333333&0,4&0,555555556&0&0,081632653\\ Lokal 122&0&0&0,555555556&0,166666667&0,183673469\\ Lokal 130&0,333333333&0&1&0&0,020408163\\ Lokal 132&0,666666667&1&0,555555556&1&0,795918367\\ Lokal 135&0,666666667&0,2&0,555555556&0,166666667&0,183673469\\ \hline \end{tabular}$

Bazując na danych znormalizowanych wyznaczymy lokale najbardziej dopasowane do zapytania klienta. Do wyliczenia podobieństwa posłużymy się metryką (odległością) euklidesową. Czym mniejszą uzyskamy wartość, tym bardziej podobne będą lokale. Analizę przeprowadzić można zakładając, że każda z pięciu wymienionych przez klienta cech jest tak samo ważna, ale można również wskazać te cechy, które powinny w większym stopniu wpływać na wynik analizy. Zbudujemy dwie macierze odległości euklidesowych:

W pierwszej macierzy znajdą się odległości euklidesowe wyliczone na podstawie równoważnie traktowanych pięciu cech;
W drugiej macierzy znajdą się odległości euklidesowe, w budowie których największe znaczenie będzie miała liczba pokoi i dystans do centrum dzielnicy.

By zbudować pierwszą macierz, w oknie macierzy podobieństwa wybieramy 5 znormalizowanych zmiennych oznaczonych jako Norm, metrykę Euklidesową i jako Identyfikator obiektu zmienną „Lokal”.

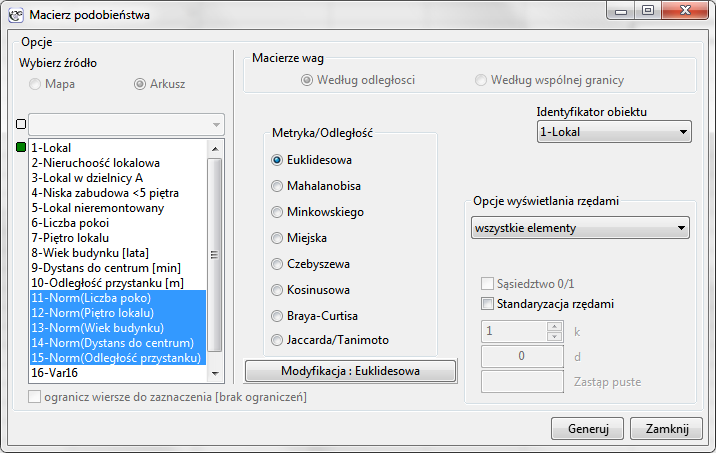
By zbudować drugą macierz, w oknie macierzy podobieństwa dokonujemy tych samych ustawień co przy budowie pierwszej macierzy, ale dodatkowo wybieramy przycisk Modyfikacja : Euklidesowa i w oknie modyfikacji wpisujemy większe wagi dla „Liczby pokoi” i „Dystansu do centru” np. równe 10, a mniejsze dla pozostałych cech np. równe 1.

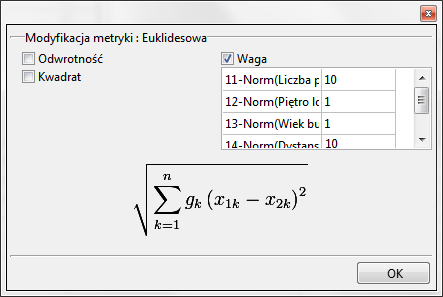
W rezultacie uzyskamy dwie macierze. W każdej z nich pierwsza kolumna dotyczy podobieństwa do lokalu szukanego przez klienta:

$\begin{tabular}{|c||c|c|} \hline Euklidesowa&\textbf{Poszukiwany}&...\\\hline \rowcolor[rgb]{0.75,0.75,0.75}Poszukiwany&0&...\\ Lokal 10&1.10&...\\ Lokal 12&1.31&...\\ Lokal 17&1.04&...\\ Lokal 35&\textcolor[rgb]{0,0,1}{0.96}&...\\ Lokal 88&1.23&...\\ Lokal 101&1.38&...\\ Lokal 105&1.18&...\\ Lokal 122&1.12&...\\ Lokal 130&1.32&...\\ Lokal 132&1.24&...\\ Lokal 135&\textcolor[rgb]{0,0,1}{0.92}&...\\ \hline \end{tabular}$

$\begin{tabular}{|c||c|c|} \hline Euklidesowa z wagami&\textbf{Poszukiwany}&...\\\hline \rowcolor[rgb]{0.75,0.75,0.75}Poszukiwany&0&...\\ Lokal 10&3.35&...\\ Lokal 12&3.84&...\\ Lokal 17&\textcolor[rgb]{0,0,1}{1.44}&...\\ Lokal 35&2.86&...\\ Lokal 88&2.78&...\\ Lokal 101&3.45&...\\ Lokal 105&3.37&...\\ Lokal 122&3.39&...\\ Lokal 130&3.43&...\\ Lokal 132&\textcolor[rgb]{0,0,1}{1.24}&...\\ Lokal 135&2.66&...\\ \hline \end{tabular}$

Według niemodyfikowanej odległości euklidesowej warunkom klienta najbardziej odpowiadać powinien lokal 35 i lokal 135. Gdy uwzględnimy wagi, najbardziej zbliżonymi do wymogów klienta będą lokale 17 i 132 - są to lokale, które w pierwszej kolejności są podobne pod względem wymaganej przez klienta liczby pokoi (3) i wskazanej odległości do centrum, mniejszy wpływ na wynik tego podobieństwa mają 3 pozostałe cechy.