Test Browna-Forsythea i Levenea

Obydwa testy: test Levenea (ang. Levene test), Levene (1960)1) i test Browna-Forsythea (ang. Brown-Forsythe test), Brown i Forsythe (1974)2), służą do weryfikacji hipotezy o równości wariancji badanej zmiennej w kilku (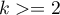$k>=2$) populacjach.

Podstawowe warunki stosowania:

Hipotezy:

\begin{array}{cl} \mathcal{H}_0: & \sigma_1^2=\sigma_2^2=...=\sigma_k^2,\\ \mathcal{H}_1: & $nie wszystkie $\sigma_j^2$ są sobie równe $(j=1,2,...,k)$$, \end{array}

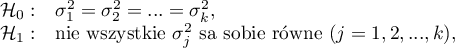
gdzie:

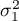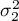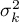$\sigma_1^2$,$\sigma_2^2$,…,$\sigma_k^2$ - wariancje badanej zmiennej w populacjach, z których pobrano próby.

Analiza polega na wyznaczaniu bezwzględnego odchylenia wyników pomiarowych od średniej (w teście Levenea) lub od mediany (w teście Browna-Forsythea), w każdej z badanych grup. Owo bezwzględne odchylenie stanowi dane, które zostają poddane dokładnie tej samej procedurze, którą wykonuje się dla analizy wariancji dla grup niezależnych. Stąd statystyka testowa przyjmuje postać:

\begin{displaymath} F=\frac{MS_{BG}}{MS_{WG}}, \end{displaymath}

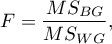
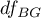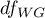Statystyka ta podlega rozkładowi F Snedecora z $df_{BG}$ i $df_{WG}$ stopniami swobody.

Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności $\alpha$:

\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}

Uwaga!

Test Browna-Forsythea jest mniej wrażliwy niż test Levenea na niespełnienie założenia dotyczącego normalności rozkładu.

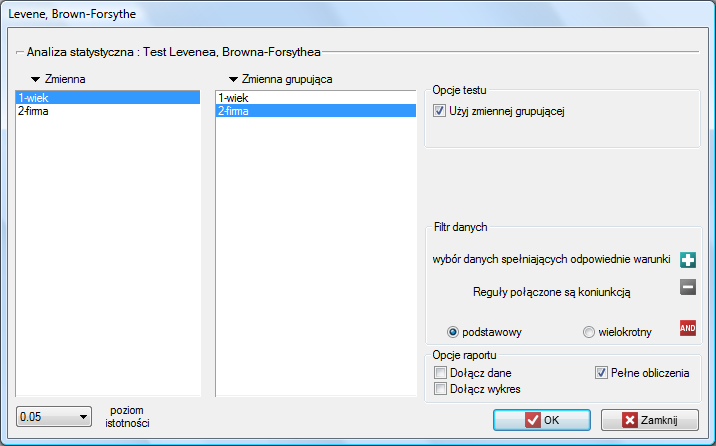
Okno z ustawieniami opcji testu Levenea, Browna-Forsythea wywołujemy poprzez menu Statystyka→Testy parametryczne→Levene, Brown-Forsythe.

1)
Levene H. (1960), Robust tests for the equality of variance. In I. Olkin (Ed.) Contributions to probability and statistics (278-292). Palo Alto, CA: Stanford University Press
2)
Brown M.B., Forsythe A. B. (1974a), Robust tests for equality of variances. Journal of the American Statistical Association, 69,364-367