pl:statpqpl:korelpl:parpl:rppl

Współczynniki korelacji liniowej

Współczynnik korelacji liniowej Pearsona 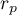$r_p$ (ang. Pearson product-moment correlation coefficient, Pearson (1896,1900)) jest wykorzystywany do badania siły związku liniowego pomiędzy cechami. Można go wyznaczać dla skali interwałowej, o ile brak jest odstających pomiarów, a rozkład reszt lub badanych cech jest rozkładem normalnym.

$\begin{displaymath} r_p=\frac{\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum_{i=1}^n(x_i-\overline{x})^2}\sqrt{\sum_{i=1}^n(y_i-\overline{y})^2}}, \end{displaymath}$

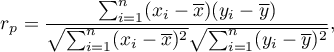
gdzie:

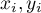$x_i, y_i$ - kolejne wartości cechy $X$ i $Y$ ,

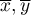$\overline{x}, \overline{y}$ - średnie z wartości cechy $X$ i cechy $Y$ ,

$n$ - liczność próby.

Uwaga!

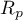$R_p$ oznacza współczynnik korelacji Pearsona populacji, natomiast 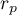$r_p$ w próbie.

Wartość 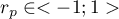$r_p\in<-1; 1>$ interpretujemy w następujący sposób:

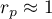$r_p\approx1$ oznacza silną dodatnią zależność liniową, tj. punkty pomiarowe leżą blisko linii prostej a wzrostowi zmiennej niezależnej odpowiada wzrost zmiennej zależnej;
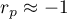$r_p\approx-1$ oznacza silną ujemną zależność liniową, tj. punkty pomiarowe leżą blisko linii prostej, lecz wzrostowi zmiennej niezależnej odpowiada spadek zmiennej zależnej;
gdy współczynnik korelacji liniowej przyjmuje wartość równą lub bardzo bliską zeru wówczas nie istnieje liniowa zależność między badanymi parametrami (ale może istnieć związek nieliniowy).

Interpretacja graficzna współczynnika 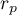$r_p$ .

$\begin{pspicture}(0,-.8)(12.5,2.5) \psline{->}(.5,0)(.5,2) \psline{->}(.5,0)(2.5,0) \rput(.8,1){*} \rput(1.7,.9){*} \rput(1,.7){*} \rput(1.3,1.6){*} \rput(1.5,1){*} \rput(1.1,.4){*} \rput(2.1,1){*} \rput(1.9,1.8){*} \rput(.2,2){$y$} \rput(2.5,-.2){$x$} \rput(1.5,-.7){$r_p\approx0$} \psline{->}(4.5,0)(4.5,2) \psline{->}(4.5,0)(6.5,0) \psline{-}(4.7,.5)(6.3,1.8) \rput(4.8,.7){*} \rput(5.3,1){*} \rput(5,.4){*} \rput(6,1.7){*} \rput(5.7,1.2){*} \rput(4.2,2){$y$} \rput(6.5,-.2){$x$} \rput(5.5,-.7){$r_p\approx1$} \psline{->}(8.5,0)(8.5,2) \psline{->}(8.5,0)(10.5,0) \psline{-}(8.7,1.8)(10.3,.2) \rput(9.6,.9){*} \rput(8.9,1.4){*} \rput(9.7,1.2){*} \rput(10.1,.2){*} \rput(9.9,.4){*} \rput(8.2,2){$y$} \rput(10.5,-.2){$x$} \rput(9.5,-.7){$r_p\approx-1$} \end{pspicture}$

Gdy jedna z badanych cech jest stała (niezależnie od zmian drugiej cechy) to nie są one związane zależnością. Współczynnika 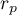$r_p$ nie można wyznaczyć.

Uwaga!

Błędem jest wyznaczanie współczynnika korelacji, gdy w próbie występują obserwacje odstające, które mogą całkowicie przekłamać wartość i znak współczynnika korelacji Pearsona, gdy próba jest wyraźnie niejednorodna, bądź też badana zależność wyraźnie przyjmuje kształt inny niż liniowy.

Współczynnik determinacji - 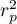$r_p^2$ . Wyraża procent zmienności zmiennej zależnej tłumaczony zmiennością zmiennej niezależnej.

Tworzony model korelacji przedstawia zależność liniową postaci:

$\begin{displaymath} Y=\beta X+\alpha. \end{displaymath}$

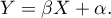
Współczynniki 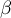$\beta$ i $\alpha$ równania regresji liniowej możemy wyznaczyć z wzorów:

$\begin{displaymath} \displaystyle{\beta=\frac{\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sum_{i=1}^n(x_i-\overline{x})^2}}, \qquad \alpha=\overline{y}-\beta\overline{x}. \end{displaymath}$

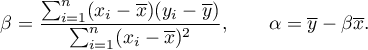
Przykład c.d. (plik wiek-wzrost.pqs)