Testowanie hipotez
Proces uogólnienia wyników otrzymanych dla próby na całą populację dzieli się zasadniczo na 2 części:
- estymację – szacowanie wartości parametrów populacji na podstawie próby statystycznej,
- weryfikację hipotez statystycznych – sprawdzanie określonych założeń sformułowanych dla parametrów populacji generalnej na podstawie wyników z próby.
Estymacja punktowa i przedziałowa
W praktyce najczęściej nie znamy parametrów (charakterystyk) dla całej populacji a dysponujemy jedynie próbką wylosowaną z tej populacji. Estymatory punktowe to charakterystyki otrzymane z próby losowej. Dokładność takiego estymatora określona jest przez jego błąd standardowy. Prawdziwe parametry populacji znajdują się w okolicy wyznaczonego estymatora punktowego. Np. parametr populacyjny średnia arytmetyczna 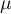 znajduje się w okolicy estymatora z próby jakim jest
znajduje się w okolicy estymatora z próby jakim jest 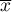 .
.
Znając teoretyczny rozkłady estymatorów próby możemy z określonym z góry poziomem ufności (1-α) szacować wartości parametrów populacji na podstawie określenia estymatorów próby losowej. Zabieg taki nosi nazwę estymacji przedziałowej, a przedział określa się mianem przedziału ufności (ang. confidence interval), samo α zaś poziomem istotności (ang. significance level).
Najczęściej przyjmuje się poziom istotności równy 0.05, 0.01 lub 0.001.
Weryfikacja hipotez statystycznych
Weryfikacja hipotez statystycznych wykonywana jest w kilku krokach:
- krok 1 Postawienie hipotez, które będą weryfikowane za pomocą testów statystycznych.
Każdy test statystyczny podaje postać ogólną hipotezy zerowej - (ang. null hypothesis) i alternatywnej -
(ang. null hypothesis) i alternatywnej - 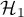 (ang. alternative hypothesis):
(ang. alternative hypothesis):
 : nie ma ważnej statystycznie różnicy między (średnimi, medianami, proporcjami , rozkładami, itp.) populacji,
: nie ma ważnej statystycznie różnicy między (średnimi, medianami, proporcjami , rozkładami, itp.) populacji,
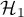 : istnieje ważna statystycznie różnica między (średnimi, medianami, proporcjami , rozkładami, itp.) populacji.
: istnieje ważna statystycznie różnica między (średnimi, medianami, proporcjami , rozkładami, itp.) populacji.
Badacz tak musi sformułować hipotezę, by była zgodna z rzeczywistością i wymogami testu statystycznego, np.:
 : odsetek kobiet i mężczyzn prowadzących działalność gospodarczą w badanej populacji jest taki sam.
: odsetek kobiet i mężczyzn prowadzących działalność gospodarczą w badanej populacji jest taki sam.
Jeśli nie wiemy, który odsetek (kobiet czy mężczyzn) w badanej populacji mógłby być większy, wówczas hipoteza alternatywna powinna być dwustronna, tzn. nie zakładamy kierunku:
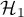 : odsetek kobiet i mężczyzn prowadzących działalność gospodarczą w badanej populacji jest różny.
: odsetek kobiet i mężczyzn prowadzących działalność gospodarczą w badanej populacji jest różny.
Może się zdarzyć (są to bardzo rzadkie przypadki), że mamy pewność, iż znamy kierunek w hipotezie alternatywnej. Wówczas można zastosować jednostronną hipotezę alternatywną. - krok 2 Sprawdzenie, która z hipotez
 czy
czy 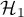 jest bardziej prawdopodobna. W zależności od rodzaju badania i charakteru zmiennych dobieramy odpowiedni test statystyczny.
jest bardziej prawdopodobna. W zależności od rodzaju badania i charakteru zmiennych dobieramy odpowiedni test statystyczny.
Uwaga 1!
Wybór testu statystycznego wiąże się przede wszystkim z wyborem odpowiedniej skali pomiarowej (interwałowej, porządkowej, nominalnej) jaką reprezentują analizowane dane, oraz z wyborem modelu badania (model zależny, model niezależny)
Pomiary danej cechy nazywamy zależnymi (powiązanymi), gdy są wykonane kilkukrotnie dla tych samych obiektów. Gdy pomiary danej cechy dokonane są na obiektach należących do różnych grup, wówczas mówimy że są to grupy niezależnych (niepowiązanych) pomiarów.
Przykłady badań w grupach zależnych:
Badanie masy ciała pacjentów przed i po terapii odchudzającej, badanie reakcji na bodziec tej samej grupy obiektów ale w dwóch różnych warunkach (np. w nocy i w dzień), badanie zgodności oceny zdolności kredytowej określonej przez 2 różne banki ale na tej samej grupie klientów itp.
Przykłady badań w grupach niezależnych:
Badanie masy ciała w grupie pacjentów zdrowych i grupie pacjentów chorych, badanie efektywności nawożenia kilku różnych rodzajów nawozów, badanie wielkości PKB dla różnych krajów itp.
Uwaga 2!
Zawarty w oknie Kreatora graf ułatwia wybór odpowiedniego testu statystycznego.
Statystyka testowa wybranego testu wyliczana zgodnie z jej wzorem podlega odpowiedniemu dla niej rozkładowi teoretycznemu.
![LaTeX \psset{xunit=1.25cm,yunit=10cm}
\begin{pspicture}(-5,-0.1)(5,.5)
\psline{->}(-4,0)(4.5,0)
\psTDist[linecolor=green,nue=4]{-4}{4}
\pscustom[fillstyle=solid,fillcolor=cyan!30]{%
\psTDist[linewidth=1pt,nue=4]{-4}{-2.776445}%
\psline(-2.776445,0)(-4,0)}
\pscustom[fillstyle=solid,fillcolor=cyan!30]{%
\psline(2.776445,0)(2.776445,0)%
\psTDist[linewidth=1pt,nue=4]{2.776445}{4}%
\psline(4,0)(2.776445,0)}
\rput(-3.6,0.2){$\alpha/2$}
\psline{->}(-3.6,0.15)(-3.1,0.04)
\rput(3.6,0.2){$\alpha/2$}
\psline{->}(3.6,0.15)(3,0.04)
\rput(1,0.5){$1-\alpha$}
\psline{->}(1,0.46)(0.55,0.35)
\rput(2.5,-0.04){wartość statystyki testowej}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img70973b37fe8a6fdf8dc5c31ade4f7228.png)
Program wylicza wartość statystyki testowej, oraz wartość dla tej statystyki (czyli część pola pod krzywą, która odpowiada wartości statystyki testowej). Wartość
dla tej statystyki (czyli część pola pod krzywą, która odpowiada wartości statystyki testowej). Wartość  pozwala wybrać spośród hipotezy zerowej i alternatywnej tę bardziej prawdopodobną. Przy czym zawsze zakładamy prawdziwość hipotezy zerowej, a zebrane w danych dowody mają dostarczyć wystarczającej ilości argumentów przeciwko tej hipotezie:
pozwala wybrać spośród hipotezy zerowej i alternatywnej tę bardziej prawdopodobną. Przy czym zawsze zakładamy prawdziwość hipotezy zerowej, a zebrane w danych dowody mają dostarczyć wystarczającej ilości argumentów przeciwko tej hipotezie:
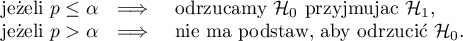
Zwykle wybiera się poziom istotności , zgadzając się, że w 5% sytuacji odrzucimy hipotezę zerową gdy jest ona prawdziwa. W szczególnych przypadkach można wybrać inny poziom istotności np. 0.01 lub 0.001.
, zgadzając się, że w 5% sytuacji odrzucimy hipotezę zerową gdy jest ona prawdziwa. W szczególnych przypadkach można wybrać inny poziom istotności np. 0.01 lub 0.001.
Uwaga!
Test statystyczny może nie być zgodny z rzeczywistością w dwóch przypadkach:

Możemy popełnić 2 rodzaje błędów: = błąd pierwszego rodzaju (prawdopodobieństwo odrzucenia hipotezy
= błąd pierwszego rodzaju (prawdopodobieństwo odrzucenia hipotezy  , gdy jest ona prawdziwa),
, gdy jest ona prawdziwa),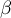 = błąd drugiego rodzaju (prawdopodobieństwo przyjęcia hipotezy
= błąd drugiego rodzaju (prawdopodobieństwo przyjęcia hipotezy  , gdy jest ona fałszywa).
, gdy jest ona fałszywa).
Moc testu to
 .
.
Wartości i
i 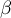 są z sobą związane. Przyjętą praktyką jest ustalenie z góry poziomu istotności
są z sobą związane. Przyjętą praktyką jest ustalenie z góry poziomu istotności  i minimalizacja
i minimalizacja 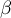 poprzez zwiększanie rozmiaru próby.
poprzez zwiększanie rozmiaru próby.
- krok 3 Opis wyników weryfikacji hipotez.