Spis treści
Testy diagnostyczne
Ocena testu diagnostycznego
Załóżmy, że przy pomocy testu diagnostycznego badamy występowanie danej cechy (najczęściej choroby) i znamy rzeczywistość (tzw. gold-standard) czyli wiemy, czy ta cecha rzeczywiście występuje u badanych osób. Na podstawie tych informacji możemy zbudować tabelę kontyngencji  :
:

gdzie:
TP - wyniki prawdziwie dodatnie (ang. true positive)
FP - wyniki fałszywie dodatnie (ang. false positive)
FN - wyniki fałszywie ujemne (ang. false negative)
TN - wyniki prawdziwie ujemne (ang. true negative)
Dla takiej tabeli możemy wyliczyć podane niżej miary.
- Czułość i swoistość testu diagnostycznego
Każdy test diagnostyczny może w niektórych przypadkach uzyskać wyniki różne od wyników rzeczywistych, na przykład test diagnostyczny na podstawie otrzymanych parametrów klasyfikuje pacjenta do grupy osób chorych na daną chorobę, bądź zdrowych. W rzeczywistości ilość osób zakwalifikowanych do powyższych grup przez test może się różnić od ilości osób rzeczywiście zdrowych i rzeczywiście chorych.
Stosowane są dwie miary oceny trafności testu diagnostycznego. Są to:
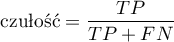
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji.
* Swoistość (ang. specificity) - opisuje zdolność wykrywania osób rzeczywiście zdrowych (bez danej cechy). Jeśli więc badamy grupę osób zdrowych, to swoistość daje nam informacje jaki procent z nich ma negatywny wynik testu.
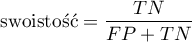
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji.
- Wartości predykcyjne dodatnie i ujemne oraz współczynnik chorobowości
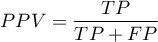
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji.
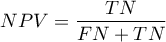
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji. Wartości predykcyjne dodatnie i ujemne są zależne od rozpowszechnienia choroby (od współczynnika chorobowości).
- Współczynnik chorobowości (ang. prevalence) - prawdopodobieństwo wystąpienia choroby w populacji, dla której przeprowadzony był test diagnostyczny.
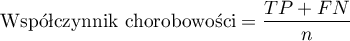
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji.
- Iloraz wiarygodności wyniku dodatniego i iloraz wiarygodności wyniku ujemnego
- WypunktowanieIloraz wiarygodności wyniku dodatniego (ang. likelihood ratio of positive test -
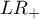 ) - miara ta pozwala na porównywanie dopasowania wyników kilku testów do tzw. gold-standard i nie jest zależna od rozpowszechnienia choroby. Jest to iloraz dwóch szans: szansy na to, że pozytywny wynik testu otrzyma osoba z grupy chorych do szansy, że ten sam efekt będzie obserwowany wśród osób zdrowych.
) - miara ta pozwala na porównywanie dopasowania wyników kilku testów do tzw. gold-standard i nie jest zależna od rozpowszechnienia choroby. Jest to iloraz dwóch szans: szansy na to, że pozytywny wynik testu otrzyma osoba z grupy chorych do szansy, że ten sam efekt będzie obserwowany wśród osób zdrowych.
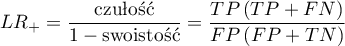
Przedział ufności dla 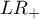 buduje się w oparciu o błąd standardowy:
buduje się w oparciu o błąd standardowy:
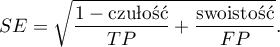
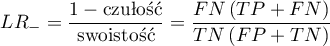
Przedział ufności dla 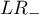 buduje się w oparciu o błąd standardowy:
buduje się w oparciu o błąd standardowy:
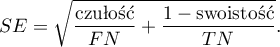
- Dokładność (ang. Accuracy (Acc)) - prawdopodobieństwo prawidłowej diagnozy przy wykorzystaniu testu diagnostycznego. Jeśli więc badana osoba otrzymała pozytywny lub negatywny wynik testu, to
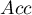 daje jej informację o tym na ile może być pewna postawionej diagnozy.
daje jej informację o tym na ile może być pewna postawionej diagnozy.
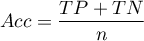
Przedział ufności budowany jest w oparciu o metodę Cloppera-Pearsona dla pojedynczej proporcji.
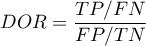
Przedział ufności dla 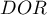 buduje się w oparciu o błąd standardowy:
buduje się w oparciu o błąd standardowy:
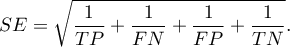
Okno z ustawieniami opcji wiarygodności diagnostycznej wywołujemy poprzez menu Statystyka zaawansowana→Testy diagnostyczne→Wiarygodność diagnostyczna
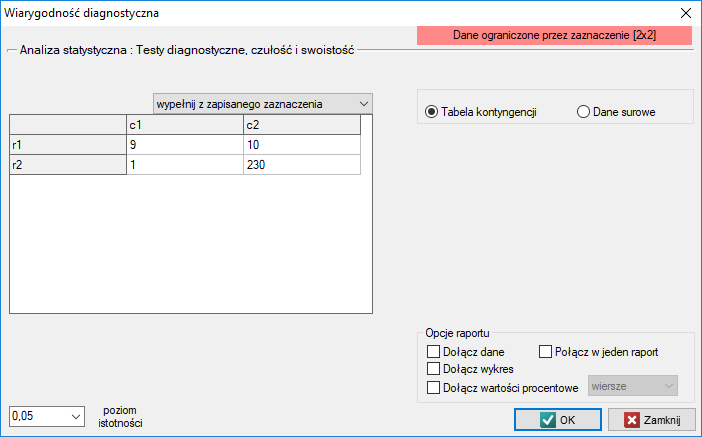
Przykład (plik mammografia.pqs)
Mammografia jest jednym z najpowszechniej stosowanych testów przesiewowych pozwalających na wykrycie raka piersi. Poniższe badanie zostało przeprowadza na grupie 250 tzw. „bezobjawowych” kobiet w wieku od 40 do 50 lat. Mammografia może wykryć ognisko raka mniejsze niż 5 mm, ale również pozwala stwierdzić zmiany, które nie są jeszcze guzkiem, a jedynie zmianą struktury tkanek. Poniżej przedstawiono przykładowy wynik badania mammograficznego.

Wyznaczymy wartości pozwalające dokonać oceny przeprowadzonego testu diagnostycznego.
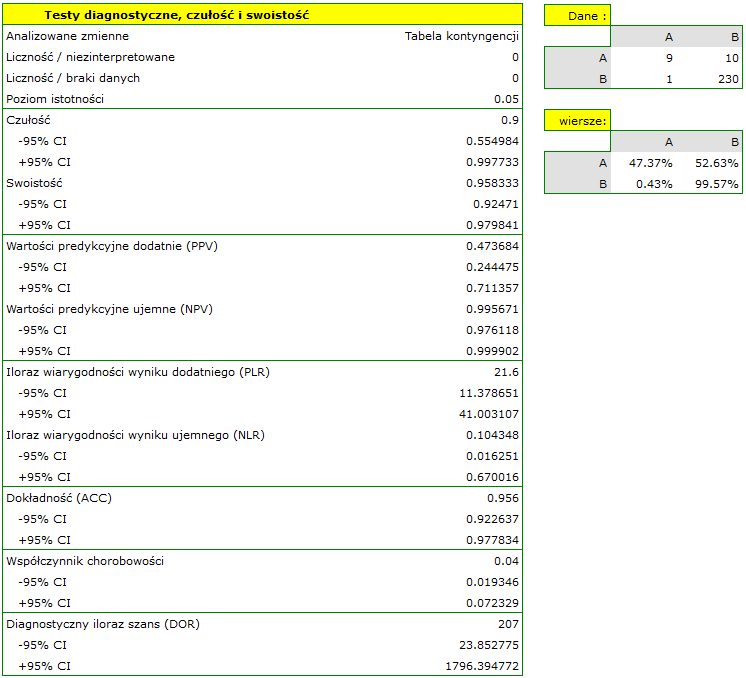
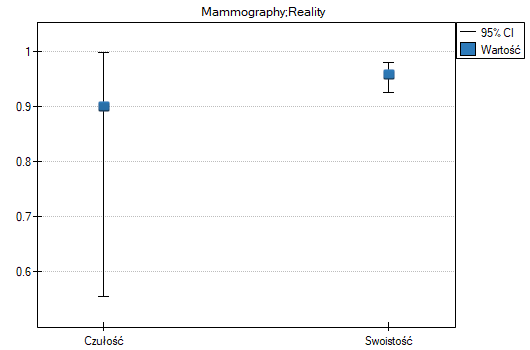
- 90% kobiet chorych na raka piersi zostało poprawnie zdiagnozowanych, czyli uzyskało pozytywny wynik mammografii;
- 95.83% kobiet zdrowych (nie chorujących na raka piersi) zostało poprawnie zdiagnozowanych, czyli uzyskało negatywny wynik mammografii;
- 4 kobiety na 100 przebadanych cierpi z powodu raka piersi;
- Kobieta uzyskująca pozytywny wynik mammografii może być w 47.3% pewna, że ma raka piersi;
- Kobieta uzyskująca negatywny wynik mammografii może być w 99.57% pewna, że nie ma raka piersi;
- WypunktowanieSzansa na to, że pozytywny wynik mammografii otrzyma kobieta rzeczywiście chora na raka jest 21.60 razy większa niż szansa, że pozytywny wynik mammografii otrzyma kobieta rzeczywiście zdrowa (nie chorujących na raka piersi);
- WypunktowanieSzansa na to, że negatywny wynik mammografii otrzyma kobieta rzeczywiście chora na raka stanowi 10.43% szansy na to, że negatywny wynik mammografii otrzyma kobieta rzeczywiście zdrowa (nie chorujących na raka piersi);
- WypunktowanieKobieta poddająca się mammografii (bez względu na uzyskany wynik) może być pewna postawionej diagnozy w 96.50%;
- Szansy na pozytwny wynik testu u kobiety która rzeczywiście choruje na raka piersi jest 207 razy większa od szansy na taki wynik kobiety zdrowej.
Krzywa ROC
 Testem diagnostycznym posługujemy się, by odróżnić obiekty z daną cechą (oznaczone jako (
Testem diagnostycznym posługujemy się, by odróżnić obiekty z daną cechą (oznaczone jako ( ), np. osoby chore) od obiektów bez danej cechy (oznaczone jako (
), np. osoby chore) od obiektów bez danej cechy (oznaczone jako ( ), np. osoby zdrowe). Aby test diagnostyczny mógł być uznany za wartościowy, powinien dawać stosunkowo niewielką liczbę błędnych klasyfikacji. Jeśli test opiera się na zmiennej dychotomicznej, wówczas właściwym narzędziem do oceny jego jakości jest analiza tabeli kontyngencji
), np. osoby zdrowe). Aby test diagnostyczny mógł być uznany za wartościowy, powinien dawać stosunkowo niewielką liczbę błędnych klasyfikacji. Jeśli test opiera się na zmiennej dychotomicznej, wówczas właściwym narzędziem do oceny jego jakości jest analiza tabeli kontyngencji 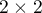 wartości prawdziwie dodatnich (TP), prawdziwie ujemnych (TN), fałszywie dodatnich (FP) i fałszywie ujemnych (FN). Najczęściej jednak testy diagnostyczne opierają się na zmiennych ciągłych lub o uporządkowanych kategoriach. W takiej sytuacji właściwym środkiem oceny zdolności testu do rozróżnienia (
wartości prawdziwie dodatnich (TP), prawdziwie ujemnych (TN), fałszywie dodatnich (FP) i fałszywie ujemnych (FN). Najczęściej jednak testy diagnostyczne opierają się na zmiennych ciągłych lub o uporządkowanych kategoriach. W takiej sytuacji właściwym środkiem oceny zdolności testu do rozróżnienia ( ) i (
) i ( ) są krzywe ROC (ang. Receiver Operating Characteristic).
) są krzywe ROC (ang. Receiver Operating Characteristic).
Często obserwuje się, że wraz ze wzrostem wartości zmiennej diagnostycznej rosną szansę na wystąpienie badanego zjawiska lub odwrotnie: wraz ze wzrostem wartości zmiennej diagnostycznej maleją szansę na wystąpienie badanego zjawiska. Wówczas przy użyciu krzywych ROC dokonuje się wyboru optymalnego punktu odcięcia, czyli pewnej wartości zmiennej diagnostycznej, która najlepiej dzieli badaną zbiorowość na dwie grupy: ( ) w której występuje dane zjawisko i (
) w której występuje dane zjawisko i ( ) w której dane zjawisko nie występuje.
) w której dane zjawisko nie występuje.
Kiedy w oparciu o badania przeprowadzone na tych samych obiektach, są zbudowane dwie lub więcej krzywych ROC, można dokonać porównania tych krzywych pod kątem jakości klasyfikacji.
Załóżmy, że dysponujemy  elementową próbą, w której każdy obiekt uzyskuje jedną z
elementową próbą, w której każdy obiekt uzyskuje jedną z  wartości zmiennej diagnostycznej. Każda z uzyskanych wartość zmiennej diagnostycznej
wartości zmiennej diagnostycznej. Każda z uzyskanych wartość zmiennej diagnostycznej 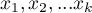 staje sie potencjalnym punktem odcięcia
staje sie potencjalnym punktem odcięcia 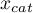 .
.
Jeśli zmienna diagnostyczna to:
- stymulanta (wraz ze wzrostem jej wartości rosną szanse na wystąpienie badanego zjawiska), to wartości większe lub równe punktowi odcięcia (
 ) zaliczamy do grupy (
) zaliczamy do grupy ( );
); - destymulanta (wraz ze wzrostem jej wartości maleją szanse na wystąpienie badanego zjawiska), to wartości mniejsze lub równe punktowi odcięcia (
 ) zaliczamy do grupy (
) zaliczamy do grupy ( ).
).
Dla każdego z  punktów odcięcia wyznaczamy wartości prawdziwie dodatnie (TP), prawdziwie ujemne (TN), fałszywie dodatnie (FP) i fałszywie ujemne (FN).
punktów odcięcia wyznaczamy wartości prawdziwie dodatnie (TP), prawdziwie ujemne (TN), fałszywie dodatnie (FP) i fałszywie ujemne (FN).


Na podstawie tych wartości każdy punkt odcięcia 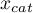 może być dalej opisany za pomocą czułości i swoistości oraz wartości predykcyjnych dodatnich (PPV), wartości predykcyjnych ujemnych (NPV), ilorazu wiarygodności wyniku dodatniego (LR
może być dalej opisany za pomocą czułości i swoistości oraz wartości predykcyjnych dodatnich (PPV), wartości predykcyjnych ujemnych (NPV), ilorazu wiarygodności wyniku dodatniego (LR ), ilorazu wiarygodności wyniku ujemnego (LR
), ilorazu wiarygodności wyniku ujemnego (LR ) i dokładności (Acc).
) i dokładności (Acc).
Uwaga!
Program PQStat na podstawie posiadanej próby wylicza współczynnik chorobowości. Wyliczony współczynnik chorobowości będzie odzwierciedlał występowanie badanego zjawiska (choroby) w populacji, gdy są to badania przesiewowe obejmujące dużą próbę reprezentującą populację. Gdy na badania skierowane są tylko osoby z podejrzeniem choroby, to wyliczony dla nich współczynnik chorobowości może być znacznie wyższy od tego współczynnika w populacji.
Ponieważ zarówno wartość predykcyjna dodatnia jak i ujemna zależy od współczynnika chorobowości, znając a priori ten współczynnik dla populacji, możemy się nim posłużyć by wyliczyć dla każdego punktu odcięcia 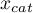 poprawione wartości predykcyjne zgodnie z wzorami Bayesa:
poprawione wartości predykcyjne zgodnie z wzorami Bayesa:
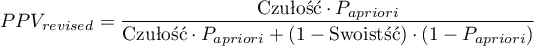
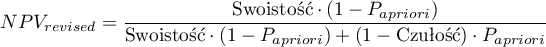
gdzie:
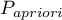 - zadany przez użytkownika współczynnik chorobowości, tzw. pre-test probability of disease
- zadany przez użytkownika współczynnik chorobowości, tzw. pre-test probability of disease

Krzywa ROC powstaje na podstawie wyznaczonych wartości czułości i swoistości. Na osi odciętych umieszczona jest 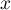 = 1-swoistość, a na osi rzędnych
= 1-swoistość, a na osi rzędnych 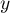 = czułość. Uzyskane punkty są ze sobą połączone. Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną analizowanej zmiennej diagnostycznej. Gdy krzywa ROC pokrywa się z przekątną
= czułość. Uzyskane punkty są ze sobą połączone. Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną analizowanej zmiennej diagnostycznej. Gdy krzywa ROC pokrywa się z przekątną  , to decyzja podejmowana na podstawie zmiennej diagnostycznej jest tak samo dobra jak losowy podział badanych obiektów na grupy (
, to decyzja podejmowana na podstawie zmiennej diagnostycznej jest tak samo dobra jak losowy podział badanych obiektów na grupy ( ) i (
) i ( ).
).
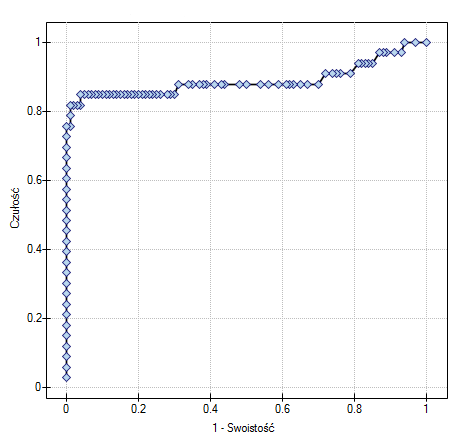
AUC(ang. area under curve) - wielkość pola pod krzywą ROC mieści się w przedziale 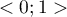 . Im większe jest pole, tym dokładniej zaklasyfikujemy obiekty do grupy (
. Im większe jest pole, tym dokładniej zaklasyfikujemy obiekty do grupy ( ) i (
) i ( ) na podstawie analizowanej zmiennej diagnostycznej. Zatem z tym lepszym skutkiem ta zmienna diagnostyczna może być wykorzystywana jako klasyfikator. Pole
) na podstawie analizowanej zmiennej diagnostycznej. Zatem z tym lepszym skutkiem ta zmienna diagnostyczna może być wykorzystywana jako klasyfikator. Pole 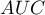 , błąd
, błąd 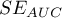 i przedział ufności dla AUC wyliczane są w oparciu:
i przedział ufności dla AUC wyliczane są w oparciu:
- metodę nieparametryczną Hanley-McNeil (Hanley J.A. i McNeil M.D. 19823)),
- metodę Hanley-McNeil zakładającą dwu-ujemny rozkład wykładniczy (Hanley J.A. i McNeil M.D. 19824)) - wyliczną tylko wtedy, gdy grupy (
 ) i (
) i ( ) są równoliczne.
) są równoliczne.
By klasyfikacja była lepsza niż losowy podział obiektów do dwóch klas, pole pod krzywą ROC powinno być istotnie większe niż pole pod prostą  czyli niż 0.5.
czyli niż 0.5.
Hipotezy:
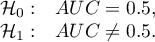
Statystyka testowa ma postać:
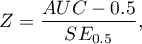
gdzie:
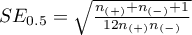 ,
,
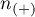 - liczność grupy (
- liczność grupy ( ), w której dane zjawisko rzeczywiście występuje,
), w której dane zjawisko rzeczywiście występuje,
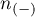 - liczność grupy (
- liczność grupy ( ), w której dane zjawisko rzeczywiście nie występuje.
), w której dane zjawisko rzeczywiście nie występuje.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Dodatkowo, gdy przyjmiemy że parametr diagnostyczny tworzy wysokie pole (AUC), możemy wybrać optymalny punkt odcięcia.
Przykład (plik bakteriemia.pqs)
Wybór optymalnego punktu odcięcia
Ten poszukiwany punkt, to pewna wartość zmiennej diagnostycznej, która optymalnie dzieli badaną zbiorowość na dwie grupy: 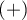 w której występuje dane zjawisko i
w której występuje dane zjawisko i 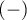 w której dane zjawisko nie występuje. Wybór optymalnego punktu odcięcia nie jest łatwy, gdyż wymaga fachowej wiedzy z zakresu tematu badań. Na przykład innego punktu odcięcia będzie wymagał test użyty w badaniach przesiewowych obejmujących dużą grupę osób np. w badaniu mammograficznym, a innego w badaniach inwazyjnych przeprowadzanych by potwierdzić wcześniejsze podejrzenie np. w histopatologii. Stosując zaawansowany aparat matematyczny możemy znaleźć taki punkt tzw. cut-off, który będzie najkorzystniejszy z matematycznego punktu widzenia.
w której dane zjawisko nie występuje. Wybór optymalnego punktu odcięcia nie jest łatwy, gdyż wymaga fachowej wiedzy z zakresu tematu badań. Na przykład innego punktu odcięcia będzie wymagał test użyty w badaniach przesiewowych obejmujących dużą grupę osób np. w badaniu mammograficznym, a innego w badaniach inwazyjnych przeprowadzanych by potwierdzić wcześniejsze podejrzenie np. w histopatologii. Stosując zaawansowany aparat matematyczny możemy znaleźć taki punkt tzw. cut-off, który będzie najkorzystniejszy z matematycznego punktu widzenia.
Program PQStat wybór optymalnego punktu odcięcia umożliwia poprzez:
- Metodę stycznej (indeks kosztów) - wyliczany w oparciu o czułość, swoistość, koszty błędnych decyzji i współczynnik chorobowości.
Błędy jakie można popełnić przydzielając badane obiekty do grupy 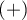 i do grupy
i do grupy 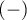 to wyniki fałszywie dodatnie (
to wyniki fałszywie dodatnie (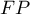 ) i wyniki fałszywie ujemne (
) i wyniki fałszywie ujemne (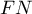 ). Jeśli popełnienie tych błędów jest tak samo kosztowne (koszty etyczne, finansowe, …), to wówczas w polu
). Jeśli popełnienie tych błędów jest tak samo kosztowne (koszty etyczne, finansowe, …), to wówczas w polu koszt FP i w polu koszt FN wpisujemy tą samą dodatnią wartość  zwykle 1. Jeśli natomiast uznamy, że jeden rodzaj błędu jest obarczony większym kosztem niż drugi, wówczas przypiszemy mu odpowiednio większą wagę.
zwykle 1. Jeśli natomiast uznamy, że jeden rodzaj błędu jest obarczony większym kosztem niż drugi, wówczas przypiszemy mu odpowiednio większą wagę.
Optymalna wartość odcięcia obliczana jest na podstawie czułości, swoistości i przy użyciu wielkości 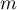 - nachylenia stycznej do krzywej ROC. Kąt nachylenia
- nachylenia stycznej do krzywej ROC. Kąt nachylenia 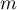 jest określany w odniesieniu do dwóch wartości: kosztów błędnych decyzji i współczynnika chorobowości. Standardowo koszty błędnych decyzji są równe 1, a współczynnik chorobowości estymowany jest z próby. Znając a priori współczynnik chorobowości (
jest określany w odniesieniu do dwóch wartości: kosztów błędnych decyzji i współczynnika chorobowości. Standardowo koszty błędnych decyzji są równe 1, a współczynnik chorobowości estymowany jest z próby. Znając a priori współczynnik chorobowości (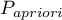 ) i koszty błędnych decyzji użytkownik może wpływać na wartość
) i koszty błędnych decyzji użytkownik może wpływać na wartość 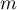 a tym samym na wyszukiwanie optymalnego punktu odcięcia. W rezultacie za optymalny punkt odcięcia uznana zostaje taka wartość zmiennej diagnostycznej, przy której wyrażenie:
a tym samym na wyszukiwanie optymalnego punktu odcięcia. W rezultacie za optymalny punkt odcięcia uznana zostaje taka wartość zmiennej diagnostycznej, przy której wyrażenie:
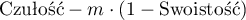 osiąga minimum (Zweig M.H. 19935)).
osiąga minimum (Zweig M.H. 19935)).
Wybrany w ten sposób optymalny punkt odcięcia zmiennej diagnostycznej zostanie ostatecznie zaznaczony na wykresie krzywej ROC.
- Indeks Youdena – Koncepcyjnie jest to maksymalna odległość pomiędzy linią będącą przekątną kwadratu o boku 1 a punktem krzywej ROC6). Indeks ten obliczany jest z wzoru:
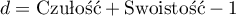
Wybrany w ten sposób optymalny punkt odcięcia zmiennej diagnostycznej zostanie ostatecznie zaznaczony na wykresie krzywej ROC.
- Odległość do lewego górnego rogu – Koncepcyjnie jest to minimalna odległość pomiędzy lewym górnym rogiem kwadratu o boku 1 (czyli miejscem w którym czułość i swoistość może być najwyższa) a punktem krzywej ROC. Indeks ten obliczany jest z wzoru:
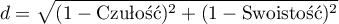
Wybrany w ten sposób optymalny punkt odcięcia zmiennej diagnostycznej zostanie ostatecznie zaznaczony na wykresie krzywej ROC.
- Wykres kosztów - prezentuje wyliczone wartości błędnej diagnozy wraz z ich kosztami. Wartości te wyliczane są zgodnie z wzorem:
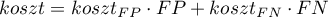
Zaznaczony na wykresie punkt, to minimum powyższej funkcji.
- Wykres przecięcia czułości i swoistości - pozwala na zlokalizowanie punktu, w którym wartość czułości i swoistości jest jednocześnie największa.
Okno z ustawieniami opcji analizy ROC wywołujemy poprzez menu Statystyka zaawansowana→Testy diagnostyczne→Krzywa ROC.
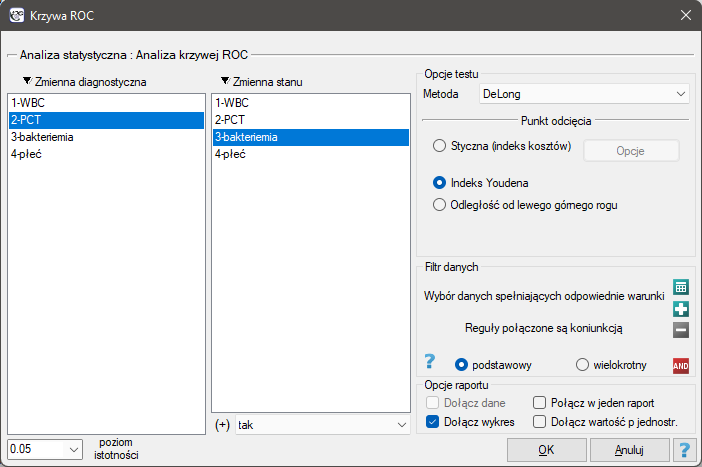
Przykład (plik bakteriemia.pqs)
Utrzymująca się wysoka gorączka u niemowlęcia lub małego dziecka bez ustalonych wyraźnych przyczyn jest wskazówką do przeprowadzenia badań w kierunku bakteriemii. Za najbardziej przydatne i wiarygodne parametry służące do przesiewowej diagnostyki i monitorowania zakażeń bakteryjnych uważa się wskaźniki:
- WBC - liczba białych krwinek (ang. white blood cells),
- PCT - prokalcytonina (ang. procalcitonin).
Przyjmuje się, że u zdrowego niemowlęcia i małego dziecka WBC nie powinno przekraczać 15 tys/µl, a PCT powinno być niższe niż 0.5 ng/ml.
Przykładowe wartości tych wskaźników dla 136 dzieci do 3 roku życia z utrzymującą się gorączką 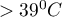 przedstawia poniższy fragment tabeli:
przedstawia poniższy fragment tabeli:
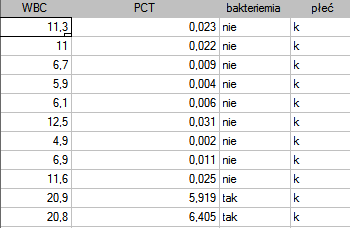
Jednym z możliwych sposobów analizy wskaźnika PCT jest przekształcenie go w zmienną dychotomiczną przez wybranie punktu odcięcia (np. 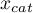 =0.5 ng/ml), powyżej którego badanie jest uznane za „pozytywne”. Jak dobry jest taki podział wskaże wartość czułości i swoistości. Chcemy wykorzystać bardziej kompleksowe podejście, czyli wyliczyć czułość i swoistość nie tylko dla jednej wartości, ale dla każdej uzyskanej w próbie wartości PCT - czyli zbudować krzywą ROC. Na podstawie uzyskanych w ten sposób informacji chcemy sprawdzić, czy wskaźnik PCT jest rzeczywiście przydatny w rozpoznawaniu bakteriemii. Jeśli tak, jaki jest optymalny punkt odcięcia powyżej którego możemy uznać badanie za „pozytywne” - wykrywające bakteriemię.
=0.5 ng/ml), powyżej którego badanie jest uznane za „pozytywne”. Jak dobry jest taki podział wskaże wartość czułości i swoistości. Chcemy wykorzystać bardziej kompleksowe podejście, czyli wyliczyć czułość i swoistość nie tylko dla jednej wartości, ale dla każdej uzyskanej w próbie wartości PCT - czyli zbudować krzywą ROC. Na podstawie uzyskanych w ten sposób informacji chcemy sprawdzić, czy wskaźnik PCT jest rzeczywiście przydatny w rozpoznawaniu bakteriemii. Jeśli tak, jaki jest optymalny punkt odcięcia powyżej którego możemy uznać badanie za „pozytywne” - wykrywające bakteriemię.
By sprawdzić, czy PCT jest rzeczywiście przydatny w rozpoznawaniu bakteriemii wyliczymy wielkość pola pod krzywą ROC i zweryfikujemy hipotezę, że:
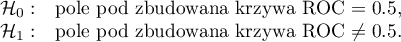
Ponieważ bakteriemi towarzyszy podwyższony poziom PCT, to wskaźnik ten uznajemy za stymulantę. W zmiennej stanu musimy określić, która wartość znajdująca się w kolumnie bakteriemia określa jej obecność, tutaj wybieramy wartość „tak”. W raporcie oprócz wyniku testu statystycznego możemy znaleźć dokładny opis każdego z możliwych punktów odcięcia.
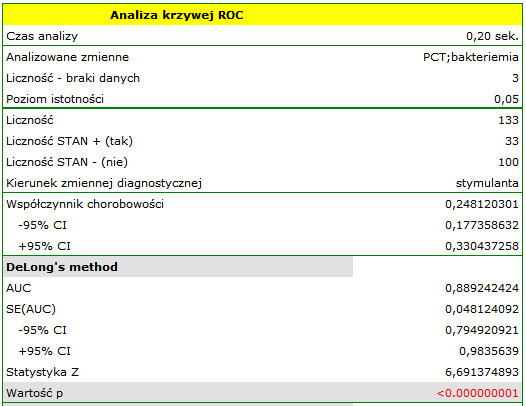
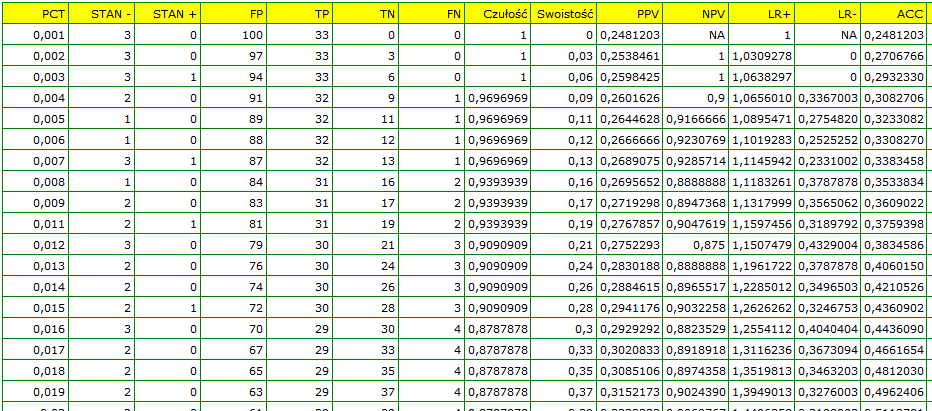
Wyliczona wielkość pola pod krzywą ROC wynosi 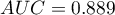 . Zatem na podstawie przyjętego poziomu
. Zatem na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
, w oparciu o uzyskaną wartość 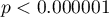 wnioskujemy, że rozpoznawanie bakteriemii przy użyciu wskaźnika PCT jest istotnie korzystniejsze niż losowy podział pacjentów na 2 grupy: chorujących na bakteriemię i nie chorujących. Wracamy więc do analizy (przycisk
wnioskujemy, że rozpoznawanie bakteriemii przy użyciu wskaźnika PCT jest istotnie korzystniejsze niż losowy podział pacjentów na 2 grupy: chorujących na bakteriemię i nie chorujących. Wracamy więc do analizy (przycisk  ), by wyznaczyć optymalny punkt odcięcia.
), by wyznaczyć optymalny punkt odcięcia.
Algorytm poszukiwania optymalnego punktu odcięcia uwzględnia koszty błędnych decyzji i współczynnik chorobowości:
koszt FN - błędna diagnoza, to koszt uznania, że pacjent nie choruje na bakteriemię mimo, że rzeczywiście jest on chory (koszty decyzji fałszywie ujemnej)- Wypunktowanie
koszt FP - błędna diagnoza, to koszt uznania, że pacjent choruje na bakteriemię mimo, że rzeczywiście na nią nie choruje (koszty decyzji fałszywie dodatniej)
Ponieważ koszty FN są znacznie poważniejsze niż koszty FP, to w polu pierwszym wpisujemy wartość większą niż w polu drugim. Uznaliśmy, że będzie to wartość 5.
Wartość PCT ma być wykorzystywana w badaniach przesiewowych, nie podajemy więc populacyjnego współczynnika chorobowości (współczynnika chorobowości a priori), który jest bardzo niski, ale pozostajemy przy współczynniku estymowanym z próby. Postępujemy tak, by nie przesunąć punktu odcięcia wartości PCT zbyt wysoko i nie zwiększyć ilości fałszywie ujemnych wyników.
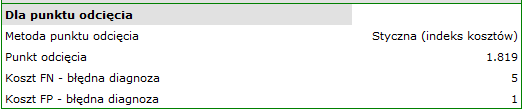
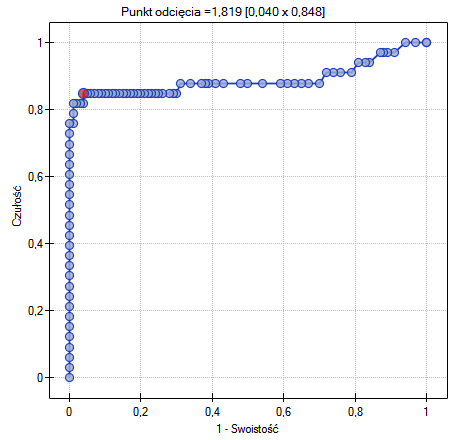
Wyznaczony optymalny punkt odcięcia PCT to 1.819. Dla tego punktu czułość=0.85 a swoistość=0.96.
Innym sposobem wyboru punktu odcięcia jest analiza wykresu kosztów i wykresu przecięcia czułości:
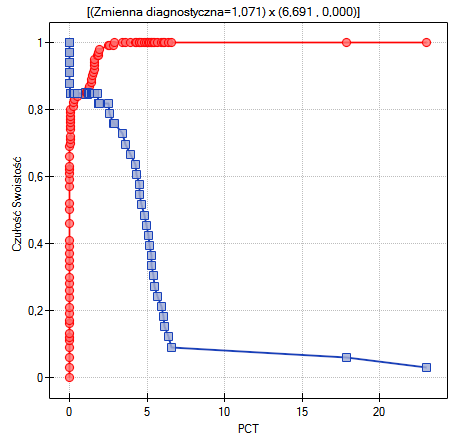
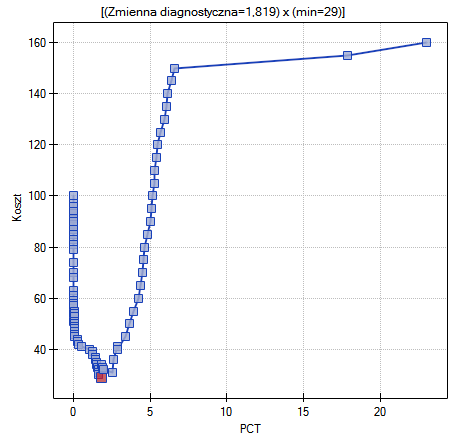
Analiza wykresu kosztów wskazuje, że minimum kosztów błędnych decyzji przypada na PCT=1.819. Natomiast wartość czułości i swoistości jest podobna dla PCT=1.071
Porównywanie krzywych ROC
Bardzo często celem badań jest porównanie wielkości pola pod krzywą ROC (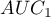 ) z polem pod inną krzywą ROC (
) z polem pod inną krzywą ROC (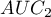 ). Krzywa ROC o większym polu, pozwala zwykle na dokładniejszą klasyfikację obiektów.
Metody służące porównaniu pól zależne są od modelu badania.
). Krzywa ROC o większym polu, pozwala zwykle na dokładniejszą klasyfikację obiektów.
Metody służące porównaniu pól zależne są od modelu badania.
- Model zależny - porównywane krzywe ROC powstają na bazie pomiarów dokonanych na tych samych obiektach.
Hipotezy:
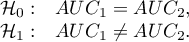
Statystyka testowa ma postać:
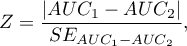
gdzie:
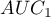 ,
, 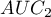 i błąd standardowy różnicy pól
i błąd standardowy różnicy pól 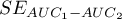 wyliczane są w oparciu o metodę nieparametryczną zaproponowaną przez DeLong (DeLong E.R. i inni 19887), Hanley J.A. i Hajian-Tilaki K.O. 19978))
wyliczane są w oparciu o metodę nieparametryczną zaproponowaną przez DeLong (DeLong E.R. i inni 19887), Hanley J.A. i Hajian-Tilaki K.O. 19978))
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji porównywania zależnych krzywych ROC wywołujemy poprzez menu Statystyka zaawansowana→Testy diagnostyczne→Zależne Krzywe ROC - porównywanie.
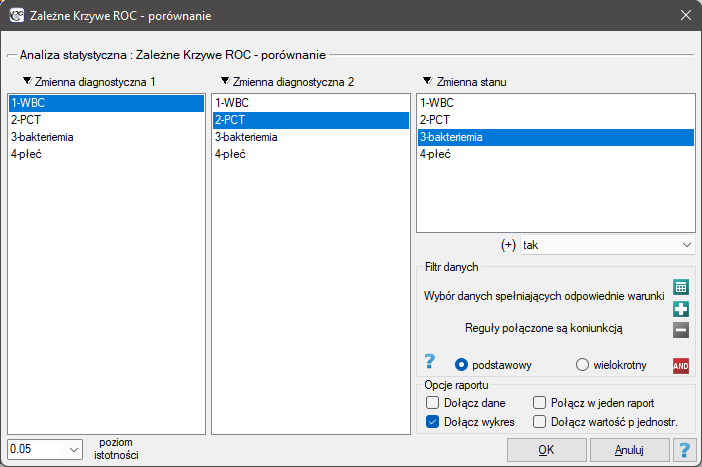
- Model niezależny - porównywane krzywe ROC powstają na bazie pomiarów dokonanych na różnych obiektach.
Hipotezy:
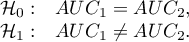
Statystyka testowa (Hanley J.A. i McNeil M.D. 19839)) ma postać:
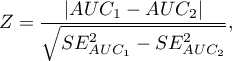
gdzie:
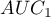 ,
, 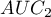 i błędy standardowe pól
i błędy standardowe pól 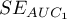 ,
, 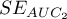 wyliczane są w oparciu:
wyliczane są w oparciu:
- metodę nieparametryczną Hanley-McNeil (Hanley J.A. i McNeil M.D. 198212)).
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji porównywania niezależnych krzywych ROC wywołujemy poprzez menu Statystyka zaawansowana→Testy diagnostyczne→Niezależne Krzywe ROC - porównywanie.
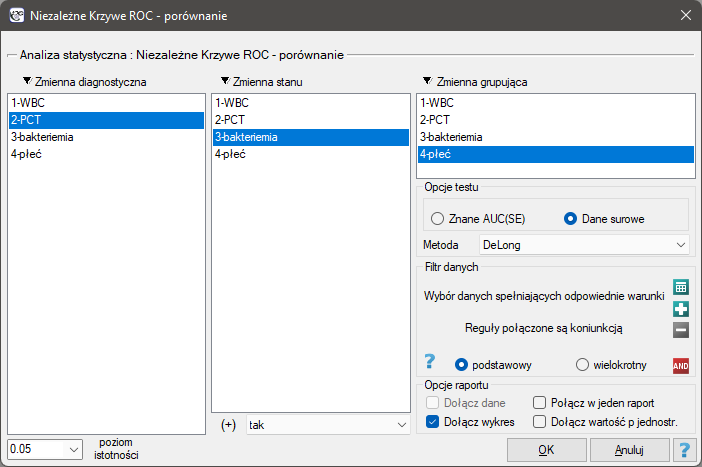
Przykład c.d. (plik bakteriemia.pqs)
Wykonamy 2 porównania:
- Zbudujemy 2 krzywe ROC, by porównać wartość diagnostyczną parametrów WBC i PCT;
- Zbudujemy 2 krzywe ROC, by porównać wartość diagnostyczną parametru PCT dla chłopców i dziewczynek.
ad1)
Zarówno parametr WBC jak i PCT jest stymulantą (wysokie wartości tych parametrów towarzyszą bakteriemii). Porównując wartość diagnostyczną tych parametrów weryfikujemy hipotezy:
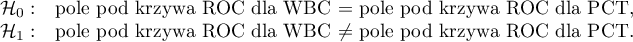
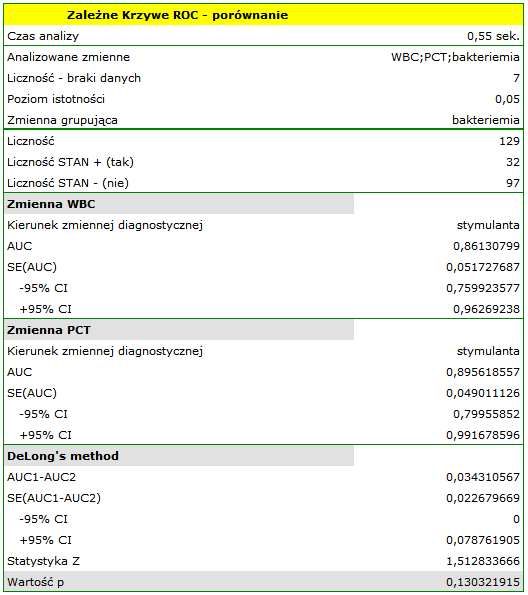
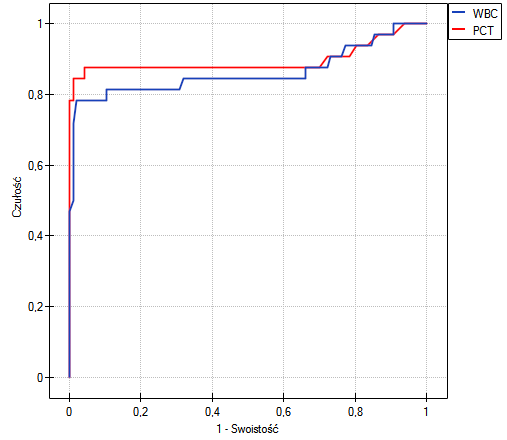
Wyliczone wielkości pól to 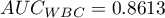 ,
, 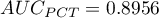 . Na podstawie przyjętego poziomu
. Na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
, w oparciu o uzyskaną wartość  0.130321915 wnioskujemy, że nie możemy wskazać, który z parametrów WBC czy PCT jest lepszy w rozpoznawaniu bakteriemii.
0.130321915 wnioskujemy, że nie możemy wskazać, który z parametrów WBC czy PCT jest lepszy w rozpoznawaniu bakteriemii.
ad2)
Parametr PCT jest stymulantą (jego wysokie wartości towarzyszą bakteriemii). Porównując jego wartość diagnostyczną dla dziewczynek i chłopców weryfikujemy hipotezy:
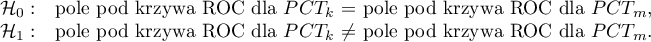
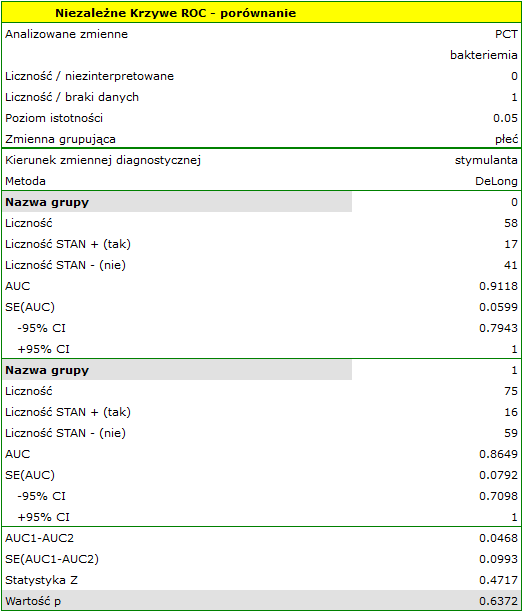
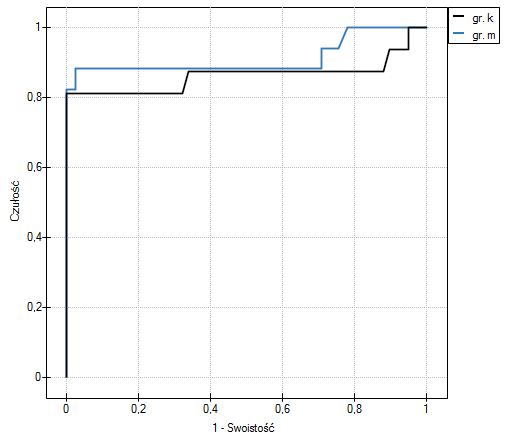
Wyliczone wielkości pól to 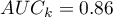 ,
, 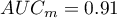 . Zatem na podstawie przyjętego poziomu
. Zatem na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
, w oparciu o uzyskaną wartość  =0.6372 wnioskujemy, że nie możemy wybrać płci, dla której parametr PCT jest lepszy w rozpoznawaniu bakteriemii.
=0.6372 wnioskujemy, że nie możemy wybrać płci, dla której parametr PCT jest lepszy w rozpoznawaniu bakteriemii.
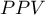 ) - prawdopodobieństwo, że osobnik miał chorobę mając pozytywny wynik testu. Jeśli więc badana osoba otrzymała pozytywny wynik testu, to PPV daje jej informację na ile może być pewna, że cierpi na daną chorobę.
) - prawdopodobieństwo, że osobnik miał chorobę mając pozytywny wynik testu. Jeśli więc badana osoba otrzymała pozytywny wynik testu, to PPV daje jej informację na ile może być pewna, że cierpi na daną chorobę.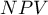 ) - prawdopodobieństwo, że osobnik nie miał choroby mając negatywny wynik testu. Jeśli więc badana osoba otrzymała negatywny wynik testu, to NPV daje jej informację na ile może być pewna, że nie cierpi na daną chorobę.
) - prawdopodobieństwo, że osobnik nie miał choroby mając negatywny wynik testu. Jeśli więc badana osoba otrzymała negatywny wynik testu, to NPV daje jej informację na ile może być pewna, że nie cierpi na daną chorobę.